梯形抗滑桩截面侧角对土拱效应的影响

2020-06-30王茂珲苏培东马云长

科学技术与工程 2020年15期

王茂珲，苏培东，马云长，邱鹏

(西南石油大学地球科学与技术学院，成都 610500)

近年来，抗滑桩的使用对于边坡过程有着日益重要的作用，抗滑桩的设置对于过程实际有着主要研究意义，对此，众多学者已经有着诸多探究[1- 4]。针对土拱效应与抗滑桩之间的关系，许多学者对此进行了研究，黄润秋等[5]基于等腰直角三角形拱的计算模型推导了矩形截面抗滑桩桩间距计算式；贾海莉等[6]认为土拱合理的模型为抛物线型，并首次提出了大小双拱传递滑坡推力的概念，认为抗滑桩正面与侧面均有发挥拱脚效能的作用；梁瑶等[7]在不同桩间距与桩的截面尺寸下，对土拱进行了实验研究，提出了在考虑土拱效应时，边坡的剩余下滑力计算方法；赵明华等[8]通过将桩土接触面的抗剪强度条件与桩后岩土体的抗剪强度条件相结合推得了圆形截面抗滑桩的桩间距计算公式；邱子仪等[9]通过对矩形桩桩后及桩侧承载力的分析，证明了桩间距随截面尺寸呈线性增大的关系；王培勇等[10]通过三角应力受压区对桩后拱与桩侧拱进行耦合建立计算模型并得出了相应桩间距计算方法；文兴等[11]通过对翼型桩的数值模拟分析，再次证明了增大桩截面后土拱效应得到加强的理论。

总结前人的研究可发现，关于土拱效应的研究主要存在以下缺陷：①对于土拱效应的研究大多依存于传统的矩形以及圆形截面的抗滑桩的桩土作用下，并未较多探讨梯形截面抗滑桩的桩土作用对于土拱效应的利弊性；②基于土拱效应的理论推导大都采用了单拱理论，并未充分考虑桩正面与侧面两部分的受力性能；③对于梯形截面抗滑桩成拱作用的关键因素并未充分考虑。

研究表明土拱的存在带来的不仅是对抗滑桩受力机制的改变，更多的是抗滑桩会反过来影响土拱的受力性能。据此，对于如何利用土拱效应从而加强抗滑桩的支护效能有更为实际的意义。梯形截面抗滑桩相较于矩形截面抗滑桩，由于桩截面侧角的存在，导致桩侧产生向上的拱脚分力，对于桩侧土拱的形成十分有利，且桩侧土拱承力性能得到提升；此外，从理论计算的角度采取双拱协同作用的传力机制也将更为合理，即双拱在梯形抗滑桩的截面特性上会产生一个闭合的桩后与桩侧双拱，两者同时承担桩后滑坡推力。据此，确定合理的桩截面侧角取值对于利用梯形截面抗滑桩发挥双拱协同作用具有研究价值。

将利用材料力学与静力学知识，基于土拱效应对梯形截面抗滑桩的桩截面侧角计算方法进行推导，进而采用数值模拟手段研究了不同的截面侧角对土拱效应的影响。

1 理论模型依据

基于水平土拱效应理论基础，参考何良德等[12]以拱脚不利位置的摩尔库伦强度条件建立的桩间距分析模型结合拱脚强度模型与双拱耦合模型进行理论推算。取特征剖面作为计算平面，设抗滑桩桩后水平推力为P，其等效均布荷载为Q；定义梯形抗滑桩截面尺寸a×d×θ，a、d、θ分别为桩截面上底长，截面高度与截面底角；桩侧土拱成拱高度为h；桩侧桩土摩阻系数为η。

需要指出的是，在梯形截面抗滑桩对于土拱的形成的模型设计上，桩身正面的影响完全取决于截面上底的尺寸长度，桩后拱的厚度与之相对应，故在截面上底一定的情况下，桩侧部分的成拱作用将直接影响双拱协同的承力的能力。据此，以桩侧抗滑能力来评价梯形抗滑桩整体抗滑能力。

N2表示拱轴线切向压力；N2y、N2x分别表示拱轴线压力的竖直以及横向分力；a表示桩截面上底尺寸；b表示桩截面下底尺寸；θ表示桩截面侧角；其余变量分别表示各点编号图1 桩侧拱脚轴向受压计算简图Fig.1 Axial compression calculation diagram of arch

桩侧单拱拱脚轴向压应力为

(1)

则桩侧提供阻滑力为

(2)

令p0对θ求导，可得：

(3)

由辅助角公式处理后可得：

(4)

2 模型的建立及参数的选取

为研究梯形截面抗滑桩桩侧特性对桩侧土拱效应的影响性，取梯形截面抗滑桩截面底角分别为45°、55°、65°、75°、85°。特别指出，由于FLAC3D有限元分析软件中无内置摩擦系数语句命令对桩土接触面进行约束，故采取截面法向刚度kn以及切向刚度ks参照文献[13-14]共同实现对摩擦系数的设定。

由于FlAC3D无梯形截面抗滑桩内置结构单元模型，为实现对梯形截面抗滑桩的桩侧特性的变换，采取ANSYS-Workbench对梯形抗滑桩-土质边坡进行三维建模，用ANSYS内置Boolean operations命令元对桩土接触模型进行整合，由Ansys-Mesh对桩土模型整体进行网格划分，如图2所示。采取 C++语句编写程序将Workbench网格模型导入FlAC3D，针对梯形抗滑桩与土体接触面问题，采取FlAC3D内置interface语句，据文献[14]方法，建立桩土接触面模型以实现接触面参数设定。模型简图及布置分别如图3和图4所示。

图2 模型网格划分示意图Fig.2 Schematic diagram model meshing

图3 模型简图Fig.3 Model diagram

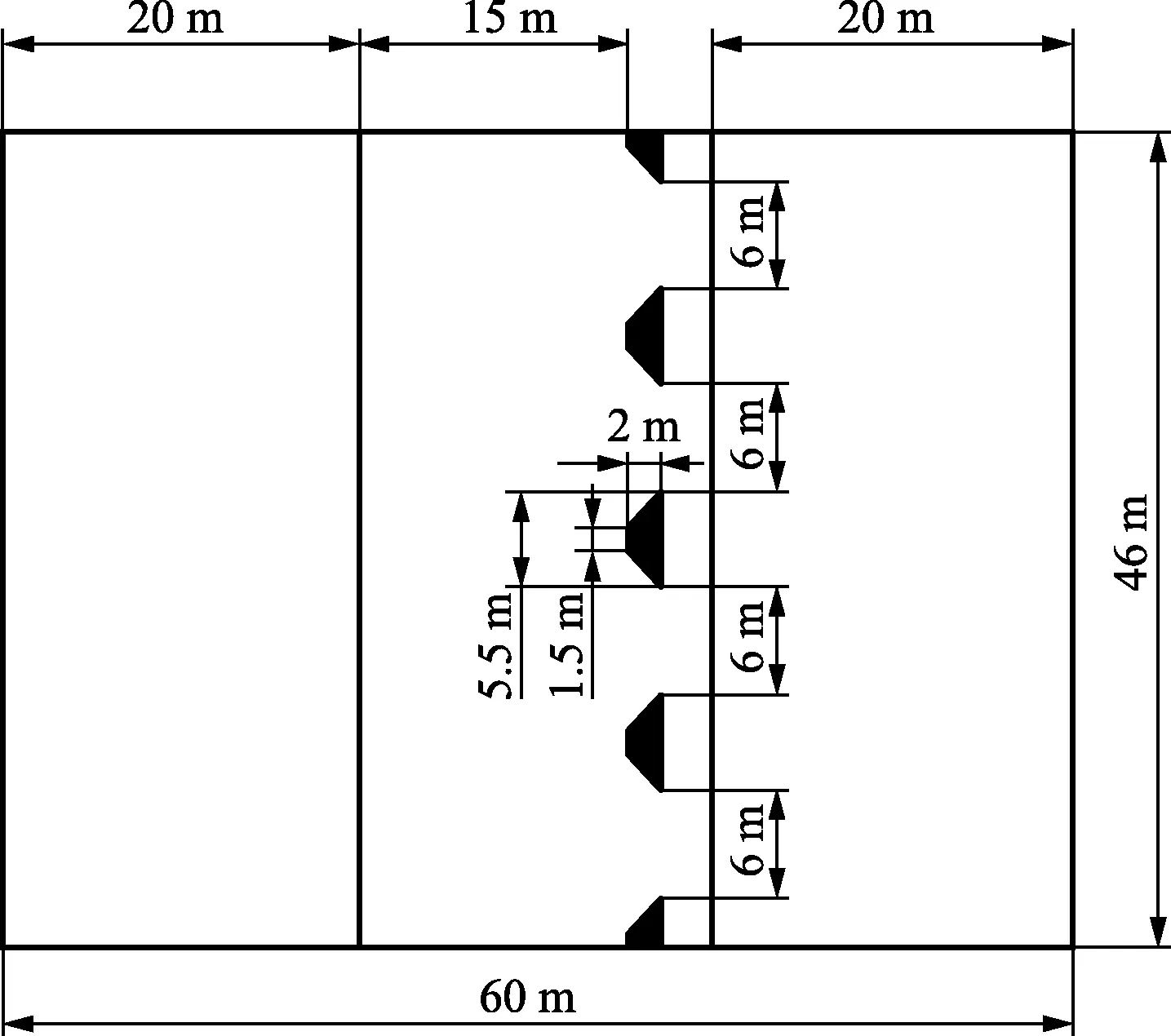
图4 抗滑桩布置示意图Fig.4 Anti-slide pile arrangement and model size

采取Mohr-Coulomb弹塑性破坏模型，桩土接触面采取摩尔库伦滑动模型。弹塑性破坏模型，桩土接触面采取摩尔库伦滑动模型。

土体参数选取如表1所示，混凝土抗滑桩参数选取如表2所示，接触面参数选取如表3所示。模型下部采取固定约束条件，容差选取(-0.1,0.1)；X，Y前后边界方向均采取固定约束，容差选取(-0.1,0.1)；模型上部为自由边界。

表1 岩土体物理力学参数Table 1 Soil physical and mechanical parameters

表2 桩土接触面参数Table 2 Pile-soil contact surface parameter

表3 混凝土抗滑桩物理力学参数

3 模拟分析

3.1 模拟步骤

FLAC3D获取网格模型后，为方便施加初始地应力时不受抗滑桩出露自由段的影响，通过FLAC3D对抗滑桩出露自由段进行单独分组，为pile；将埋入段与坡体共同划分一组，为soil and pile；土质边坡划分为一组，为soil。如图5所示，计算初始地应力时，通过null命令将出露自由段去除，对soil and pile与soil进行统一参数施加，均视为土。

图5 桩土分组示意Fig.5 Piled-soil grouping

对中间每组侧角模型，沿中间两桩的桩间跨中x方向布设位移监测点，如图6所示，截取=23水平面，分别选取x=23 m、24 m、25 m、26 m、27 m、28 m、29 m、30 m、31 m，32 m、33 m、34 m、35 m、36 m的14个跨中点位进行位移监测。

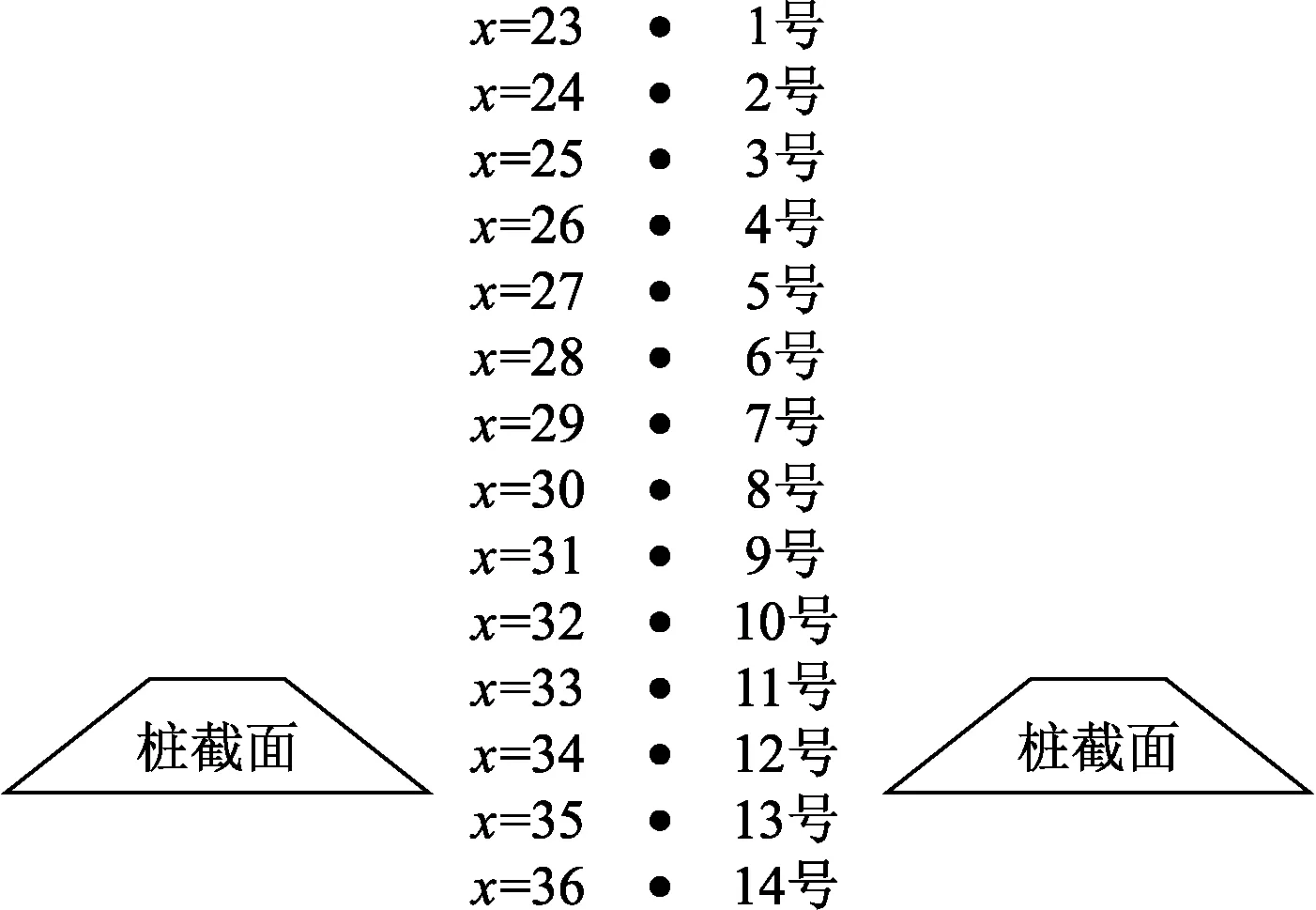
图6 跨中轴线监测点布置Fig.6 Schematic diagram of monitoring points on the central axis

图7 45°截面侧角下主应力云图Fig.7 Principal stress cloud diagram at 45° section side angle

3.2 不通截面侧角下的应力云图分析

从理论计算的角度45°～55°侧角在梯形截面抗滑桩的桩土成拱效应过程中可以充分发挥双拱协同作用。保持桩截面上底，桩间距且截面高度一定的情况下，通过五组不同桩截面侧角的数值模拟，以滑动面推力方向为界做水平切面，得到不同侧角下的桩土作用结果。各截面侧角下主应力云图如图7～图11所示。由图7(a)～图11(a)可以看出，从45°侧角开始，参照大主应力云图，桩间土拱效应与桩后土拱效应应力等值区复合程度较高，无明显应力区分化，桩侧土拱应力等值区厚度基本覆盖桩侧部分，证明该角度能充分发挥并加强桩侧部分对于桩侧土拱形成的能力，换言之，桩侧部分的成拱性能得到了提升。桩后土体由远到近，压应力逐渐增大，直至拱前应力等值区，即拱后缘附近达到压应力最大。拱前缘土体逐渐呈受拉状态，说明桩后土体推力传至土拱后，随着拱内土体的压实发育，剪应力发生迁移，桩后推力由土拱开始分担并传至桩侧受荷面与桩正面受荷面上，桩身为弹性模量足够大的近似刚体模型，桩间双拱未发生失稳，则成为阻隔压应力继续沿x方向传导的天然屏障。

55°侧角下(图8)，桩侧受荷面及桩正面受荷面形成的双拱仍呈高度复合，保持应力等值状态。但可见土拱内部等值区压应力明显增大且拱高开始减小，说明拱内土体整体受力压实继续发育，开始承担拱后推力。由小主应力云图可见，桩后及桩侧部分双拱协同作用明显，桩侧部分压应力开始集中，性能得到体现。

当桩侧角达到65°，直至85°侧角，桩后土拱应力等值区开始消失，桩侧土拱应力等值区高度显著增大。在截面上底、截面高度、桩间距及桩土接触面摩擦系数一定的情况下，桩侧角的增大即减小桩侧沿x方向受力分量，桩侧摩阻性能开始被放大，桩截面正面受荷面性能开始被缩小。而桩侧土拱应力等值区后缘土体沿x方向应力分布呈现不均匀状态，说明桩侧土体成拱发生应力偏转，土拱开始失稳。

图8 55°截面侧角下主应力云图Fig.8 Principal stress cloud diagram at 55° section side angle

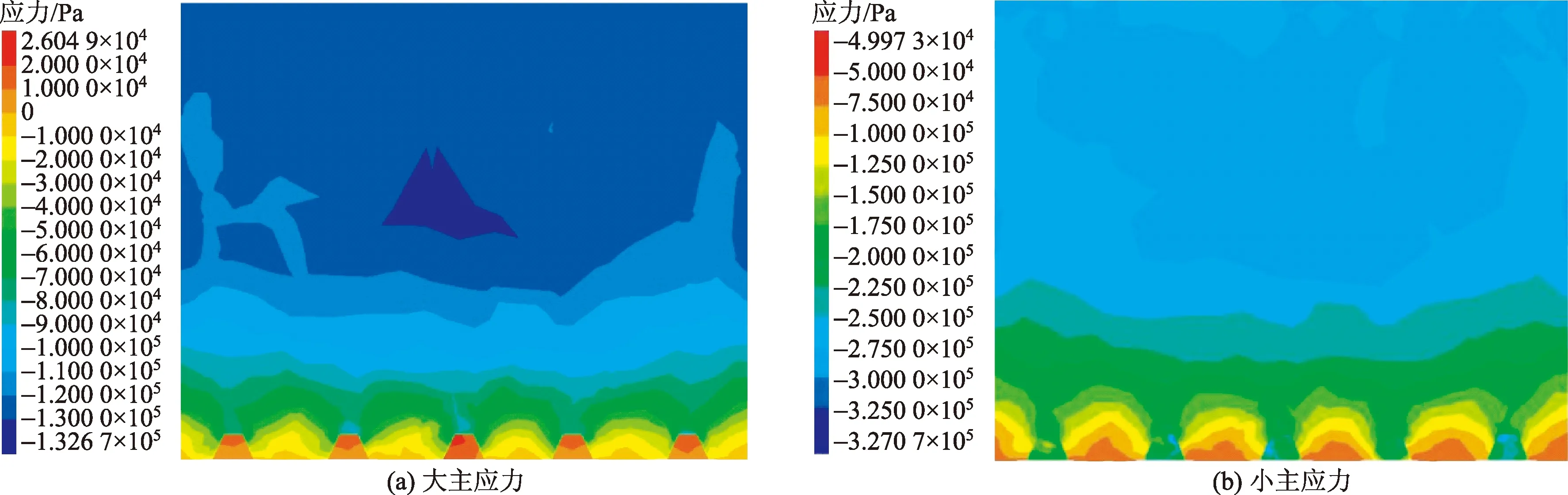
图9 65°截面侧角下主应力云图Fig.9 Principal stress cloud diagram at 65° section side angle

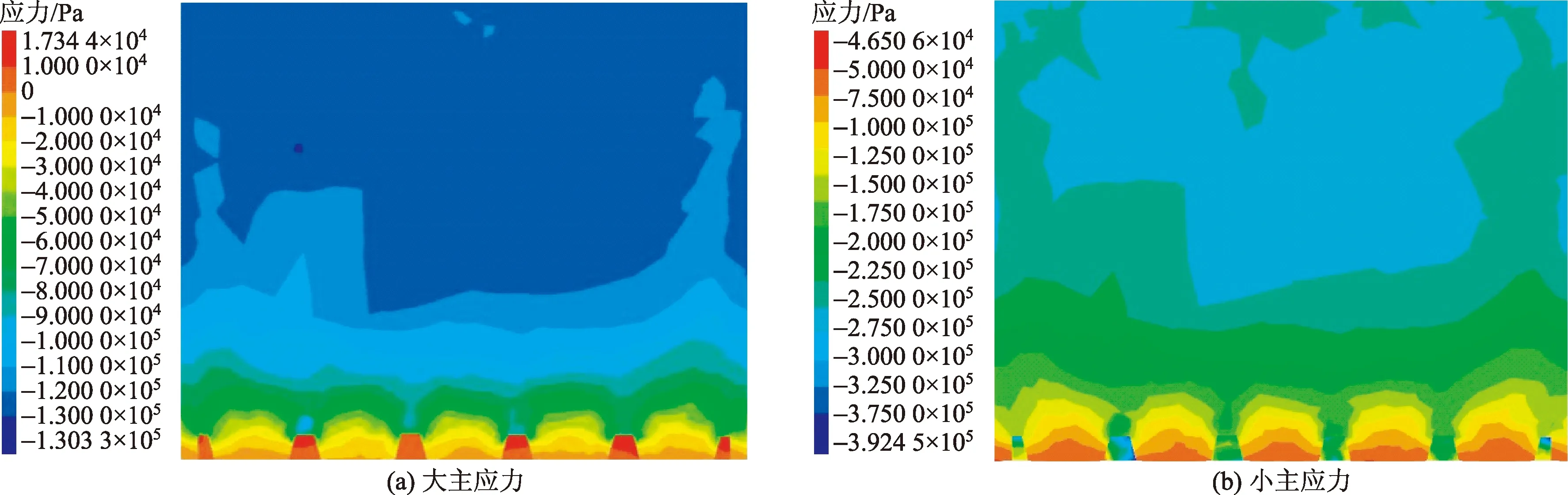
图10 75°截面侧角下主应力云图Fig.10 Principal stress cloud diagram at 75° section side angle

由图7～图11可以看出，大小主应力随着桩截面侧角的增加，桩间土红色区域即拉应力(正值)区域，均在靠近桩背处范围最大后逐渐增大至峰值。而压应力(负值)，于桩间和桩后应力等值线均呈拱形分布，拱圈上压应力值从桩间到桩背方向逐渐增加，等值线之间的密度逐渐减小，土拱厚度由厚变薄，并且土拱拱形从抛物线状逐渐消散。从θ=45°、θ=55°截面上应力云图可以看出，桩侧和桩背应力值明显大于桩间土拱区域应力，即滑坡推力经土拱结构有效传递到抗滑桩上，形成以桩侧和桩背共为拱脚的桩侧土拱和桩后土拱；从θ=55°～85°应力云图可知，桩侧及桩后应力值与土拱应力等值区应力差值逐渐减小，即滑坡推力未经土拱结构有效传导至抗滑桩周。综合得知：当梯形截面抗滑桩上底，截面高度以及桩间距布设与桩土接触面摩阻系数保持一定时，45°～50°的截面侧角有利于加强桩侧与桩后受力面性能，使分别以桩侧与桩背面作为拱脚的双拱发挥协同作用。在此取区间段以外的侧角角度，会削弱双拱协同传力的机制，仅仅促使单拱的发育会增大桩周土体绕流效应从而导致土拱传力机制的削弱或消失。

3.3 监测点位移分析

从45°侧角跨中位移监测点位移变化情况分析，如图12(a)所示，跨中各点位移变化均从 step=2 500 开始趋于稳定，1～9号点位，各点位位移变化曲线增势基本一致，但从step=2 200～2 500段位移处于稳定状态，之后继续增大，位移增长率基本保持一致；从11号点开始，位移峰值发生突增，但step=0～2 500其间增长率与1～10号点位基本保持一致。说明step=0～2 500其间于跨中x=33 m以上土拱开始形成，拱厚开始发育，随着拱内土体压实，拱间土及其拱后土体位移被限制，随着桩后推力逐渐加大，土拱拱厚被继续压缩，直至稳定后，跨中各点位移开始趋于稳定。据此可判断，拱体再跨中的拱前缘位置大概出现在桩截面顶部连线跨中以上附近，特别指出，x=34 m、35 m、36 m三点处于拱体前缘，由于桩间土拱的发育，拱前土体呈现拉应力集中，位移出现陡增；通过加权平均法确定拱厚约为x=33 m以上7 m，拱顶处于x=28 m附近。以此类推，侧角为55°、65°、75°、85°桩侧拱厚发育分别如图12(b)～图12(e)所示。

图12 各截面侧角下跨中位移监测点位移变化Fig.12 Displacement change of mid-span displacement monitoring point under each section side angle

如图13所示，通过应力等值云图得出的桩侧土拱拱高与对桩间跨中轴线布位移监测点采用加权平均得出的拱高变化基本拟合，究其关系曲线的变化可知，在截面侧角为40°～55°，拱高达到极小值，随桩侧角增大，此时梯形截面无限趋近于同上底的矩形截面，桩侧摩阻力作为拱脚反力，对桩侧土拱的形成开始发挥主要受力性能。此过程在保持截面上底一定的前题下，截面下底相较低侧角度的梯形截面的下底相较于之前的桩间距比值陡然下降，由于桩沿y方向可近似看作无位移刚体，在桩侧摩阻上限一定的情况下，随桩后推力的增大，桩间土在桩侧接触面法向应力不断增大，摩阻力作为拱脚反力不断增大，出现拱脚拱厚，跨中拱薄的应力等值区，出现拱高而薄的现象，且桩截面正面受荷面相较于桩侧丧失成拱性能，未充分发挥其端承式土拱反力支座的受力性能。

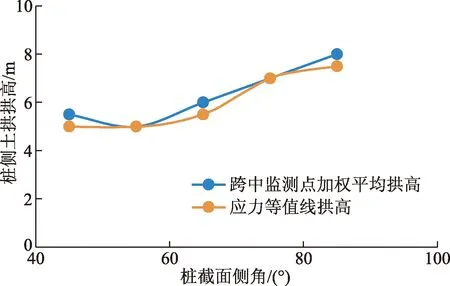
图13 截面侧角与拱高关系曲线Fig.13 Cross section angle and arch height curve

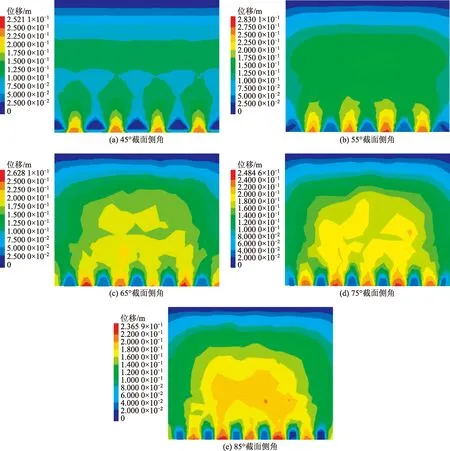
图14 各截面侧角下x方向位移云图Fig.14 The x-direction displacement cloud diagram at each section side angle

3.4 不同截面测角下的位移云图分析

截取z=23 m水平切片，对x方向位移位移云图进行分析，由图14(a)可知，45°截面侧角下，桩土位移与桩间跨中向两边分化明显，随跨中向两边位移逐渐增大，桩间x方向位移最小，说明此在截面侧角下，桩间土拱成拱效应于拱后缘有效承担了桩后推力，改变了原有土压力的传力机制，剪应力偏转发育明显；于55°截面侧角下，由图14(b)可知，x方向位移仍于桩间跨中产生明显分化，随着x的增大而增大，位移临界点对比45°截面侧角下的位移临界点x减小，说明在此截面侧角下，桩间土拱拱内土体压实效应继续发育，由于桩侧与桩正面仍发挥拱脚支座作用并提供足够的支座反力，故拱高被相对压缩，双拱协同作用仍承担传递桩后推力的作用；随着截面侧角提高至65°，如图14(c)所示，位移云图等值区密度沿桩间跨中陡然增大，且位移临界点x差值徒增，结合该侧角应力云图变化情况，此过程的位移变化印证了截面正面受荷面开始丧失作为桩后土拱拱脚的性能，双拱协同作用开始消失，桩侧性能开始被放大，从而致使桩侧土拱开始作为主要传力的桥梁，且其拱高相较于双拱协同作用时突增，直至75°截面侧角下，如图14(d)所示，桩侧土拱效能达到峰值，至85°侧角下，如图14(e)所示，桩间跨中内部开始明显出现位移分化区，说明此时的桩侧成拱效应已不足以承担桩后推力，桩侧土拱开始失稳。综合其x方向位移变化情况，再次印证了侧角45°～55°的合理性，其对于双拱协同效应的发生有着偏健康的作用。

3.5 接触面位移增量对比

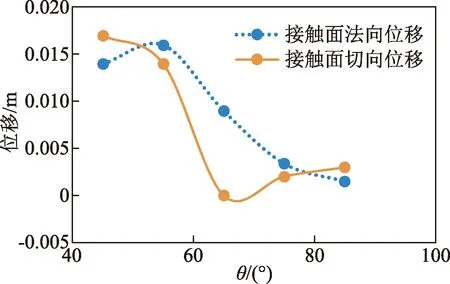
图15 不同截面侧角下的桩侧桩土接触面位移对比Fig.15 Displacement comparison of pile-soil contact surface under the side angles of different sections

对各侧角下模型下的桩土接触面桩侧部分中点分别设置接触面法向与切向位移观测点。截取稳定step=10 000的各截面侧角下的接触面法向位移与切向位移，如图15所示，发现45°～55°侧角下的接触面法向位移明显增大，切向位移相对减小，证明了截面侧角在此区间段，有利于土拱效应的发生已经拱体自身的压实，发挥传力的效能优秀。过55°截面侧角后，桩土接触面法向位移与切向位移均开始下降，但65°截面侧角下，接触面切向位移开始增加，桩侧性能开始放大，为抵抗桩间土体挤出，桩侧摩阻作用被压榨，直至桩间土挤出，而此期间接触面法向位移自然减小，此现象侧面说明了双拱协同效能的丧失到桩侧土拱单独受力直至土拱丧失稳定性的过程，与3.4节分析结果吻合。