基于卷积神经网络的脑电信号分类

李玉花, 柳 倩, 韦 新, 程永强*, 李海芳

(1.太原理工大学信息与计算机学院，太原 030600；2.西安交通大学社会心理学研究所，西安 710000)

脑电信号(EEG)是生物电信号中的一种，蕴含着丰富的生理和心理信息，脑电活动与脑区域、脑状态有着密切的联系。通过记录脑电信号，可以检测大脑活动[1]，也是了解人脑信息处理过程的重要手段之一。对脑电信号进行深入的分析处理可以为生物医学、临床疾病诊断提供重要依据[2]。脑电信号的研究应用主要集中在以下几方面：脑机接口、情绪情感识别、心理生理疾病的诊断与预测[3]以及大脑活动的检测与区分[4]。在对脑电信号的分析处理中，脑电信号的分类是其中最关键的技术。近年来，脑电信号分类的方法主要有：S变换[5]结合卷积神经网络(CNN)[6]，快速独立分量分析(fast independent component analysis，Fast ICA)结合卷积神经网络，功率谱熵、样本熵和Hurst指数等非线性特征提取结合相关向量机(relevence vector machine, RVM)[7]，基于稀疏回归和加权朴素贝叶斯分类器的方法[8]，共空间模式(common space model,CSP)结合卷积神经网络[9]，基于固有模态分解算法(empirical mode decomposition,EMD)与CNN的方法[10]，在纯人工神经网络方面多数为CNN[11-12]，还有一部分为循环神经网络(recurrent neural network，RNN)及RNN的升级版长短时记忆网络[13](long short-term memory，LSTM)。目前脑电信号分类模型中，分类效果最好的是CNN。在癫痫自动检测的脑电信号分类中平均准确率达到了88.67%[14]，在想象左右手运动脑电信号分类中准确率达到了93.12%[12]，效果均优于传统脑电分类方法。

但是现有的卷积神经网络脑电信号分类模型还是以其他特征为依托，需要对预处理后的信号再处理得到一定的特征后再输入CNN进行分类，分类效率低。本文针对以上问题，提出了一种多尺度卷积核CNN脑电分类模型。首先，通过在输入数据前添加系数矩阵，代替传统手工提特征的步骤，其次，设置不同参数的多尺度卷积核CNN确定网络模型，最后使用高原脑电数据集做分类实验检测模型的分类效果，验证该模型的可行性。

1 数据集与数据预处理

1.1 脑电数据

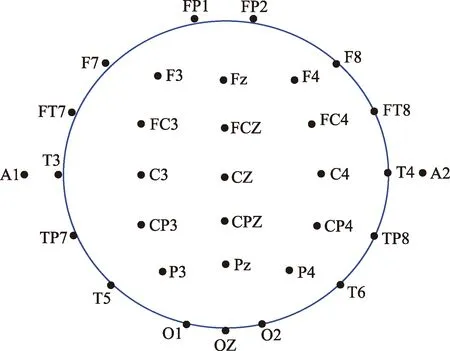
图1 电极安放空间示意图Fig.1 Electrode placement space

实验数据采集对象为来自四个不同海拔地区的80名志愿者，四个地区分别为渭南(海拔400 m)、林芝(海拔3 100 m)、拉萨(海拔3 600 m)和那曲(海拔4 500 m)。实验使用NeuroScan公司的32导电极帽进行数据采集，按照国际10%～20%电极安放法放置，即：以鼻根到枕外隆凸尖的前后连线作为矢状线，以双耳前凹之间的左右连线为冠状线，两条线的焦点在头顶Cz电极处，左侧为奇数电极，右侧为偶数电极，电极分别为前额叶(FP1、FP2)，额叶(F3、F4、F7、F8)，前颞叶(FT7、FT8)，前额中部(FC3、FC4、FCZ)，颞叶(T3-T6)，顶叶(P3、P4)，中央(C3、C4)，枕叶(O1、O2、OZ)，顶颞叶(TP7、TP8)中枕叶(CP3、CP4、CPZ)，加上前后位上的额中点(Fz)、顶点(Pz)以及两个耳电极(A1、A2)共32个电极，电极之间间隔按矢状线的10%～20%的比例确定。空间示意图如图1所示。采集图1中的32个电极处的脑电信号。采样频率为1 000 Hz,阻抗低于5 kΩ，参考电极物理连接在左、右侧乳突[15]。采集数据时，被试在安静的室内闭眼静坐，限制头部运动，避免吞咽以及眼睛闪烁。

1.2 数据预处理

实验数据离线处理时以所有电极的平均电位作为参考，使用BP 2.0平台上的Ocular Correction 功能去除眼电干扰，使用Raw Data Inspection 功能去伪迹，其中涉及的参数选择包括：电压梯度值最大为50 μV/ms，时间间隔内电压变化绝对值最大设置为200 ms 内，至多变化200 μV，电压变化的最低活跃度设置为100 ms 内，至少变化0.5 μV[15]。

采集到的数据有：渭南、林芝、拉萨和那曲各60、30、16、38个样本，每个海拔的样本为时间长度不等的45～70 s的脑电数据段，每段有4.5×104～7×104个采样点。使用的网络分类模型为CNN，为了适应CNN的输入，需要将预处理后的脑电数据进行格式转换，即将EEG数据转换成MATLAB格式的二维数字矩阵，最后将转换后的数据按采样点切分成32×81大小的图片，最终得到的数据量为渭南4.2×104、那曲2.7×104、林芝2.1×104、拉萨 1.1×104个，待后续输入网络使用。

2 卷积神经网络

2.1 经典CNN

经典CNN模型一般结构为输入层、交替叠加的卷积层和池化层、全连接层和分类器。CNN通过卷积层从输入数据中提取局部特征，通过池化层将提取到的特征降维简化，最后利用全连接层与分类器输出分类结果。经典CNN通过前向传播输出卷积层中可学习卷积核与本层输入的卷积，作为下一层的输入，通过误差的反向传播修正各层的网络权值和偏置。其前向传播公式为

(1)

2.2 多尺度卷积核CNN

2.2.1 CNN卷积层改进

经典CNN在每一个卷积层中使用单一尺寸的卷积核，卷积核尺寸的大小直接影响着网络性能的好坏，感受野太大超出卷积核可以表达的范围，感受野太小，卷积核无法提取到有效的局部特征[17]。因此经典CNN依靠多层卷积池化提取不同的基层特征提高分类准确率，但是网络层数的增加会使网络参数成倍增长，不利于网络的快速收敛，严重影响网络性能。

针对以上问题，对经典CNN的卷积层进行改进，即在CNN的卷积层上增加不同尺度的卷积核，以拓展卷积层提取特征的视野维度，减少网络层数，降低网络的复杂度，极大减少了需要训练的权值参数，适用于样本量小的数据集。改进前后CNN卷积层对比如图2所示。

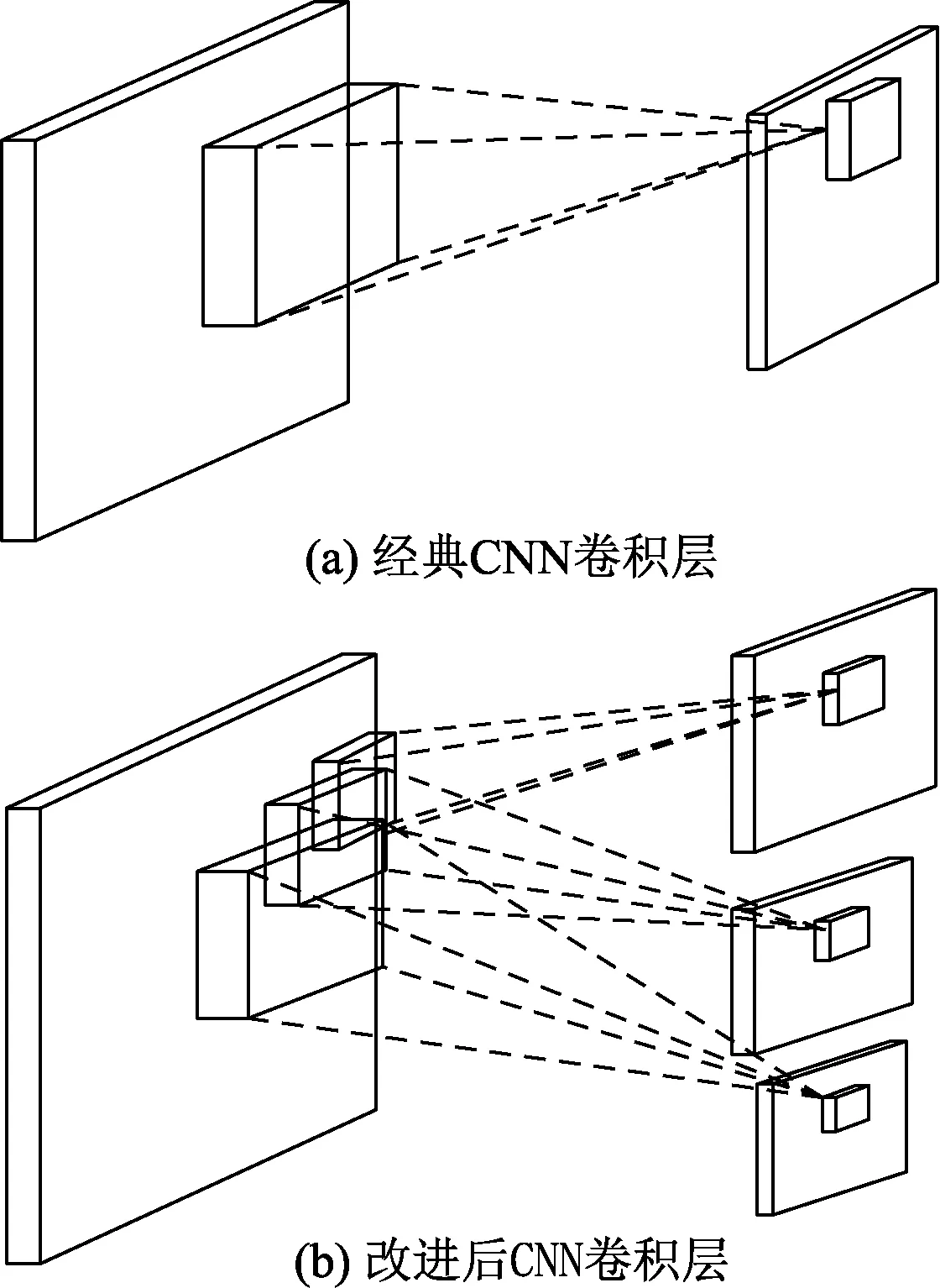
图2 改进前后卷积层结构对比Fig.2 Comparison of convolutional layer structure before and after improvement

2.2.2 多尺度卷积核CNN网络模型结构

由于经过预处理和格式转换的脑电数据为二维的数字矩阵，不像图像数据那样有丰富的信息，只能从时间维度和空间通道维度提取一些特征来识别，而深度卷积神经网络的最佳对象为图片、影视图像等，对于脑电之类的时间序列，隐含层的增加在特征提取上意义不大，不仅不会使分类准确率提升，还会导致需要训练的权值参数激增，而数据量的不足会使参数训练不充分，导致分类效果变差。因此针对所使用数据的特性，对CNN改进后，提出了多尺度卷积核卷积神经网络脑电分类模型。

该网络模型一共包含5层，第一层为输入层，输入数据为32×81大小的图片；第二层为卷积层，包含三种尺度的卷积核；第三层为池化层；第四层为全连接层，将池化后的数据铺平，为最后的分类做准备；第五层为输出层，由Softmax分类器输出，可以实现多分类。输入采用N×T的形式，其中N=32表示通道数，T=81表示采样点数，因此输入矩阵为32×81。脑电分类模型的总体结构如图3所示。多尺度卷积核CNN模型的前向传播与经典CNN相同，如式(1)所示，损失函数如式(2)所示：

(2)

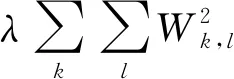
(3)

式(3)中:k表示类别数;zj表示第j个类别的线性预测概率;zk为k个类别的线性预测概率之和;fj(z)为每一类的归一化预测结果。

2.2.3 输入数据特征粗提取

传统CNN脑电分类模型中特征提取与信号分类是分离的，需要进行专门的特征提取，如文献[9]使用CSP算法提取数据特征作为CNN的输入，文献[10]使用EMD算法得到特征，还有一些使用的是差分熵(differential entropy,DE)[18]计算结果作为特征，这些都是在预处理后，根据数据特性计算某些参数指标作为下一阶段分类的输入。

而通过在输入数据前添加32×1的W系数矩阵(32对应输入数据的通道数N)达到对数据特征的初步提取，省去了繁琐的参数计算，同时W系数矩阵中的数值不需要人为设定，只需要给定一组初始的随机值，后续会随着网络的迭代自动更新。

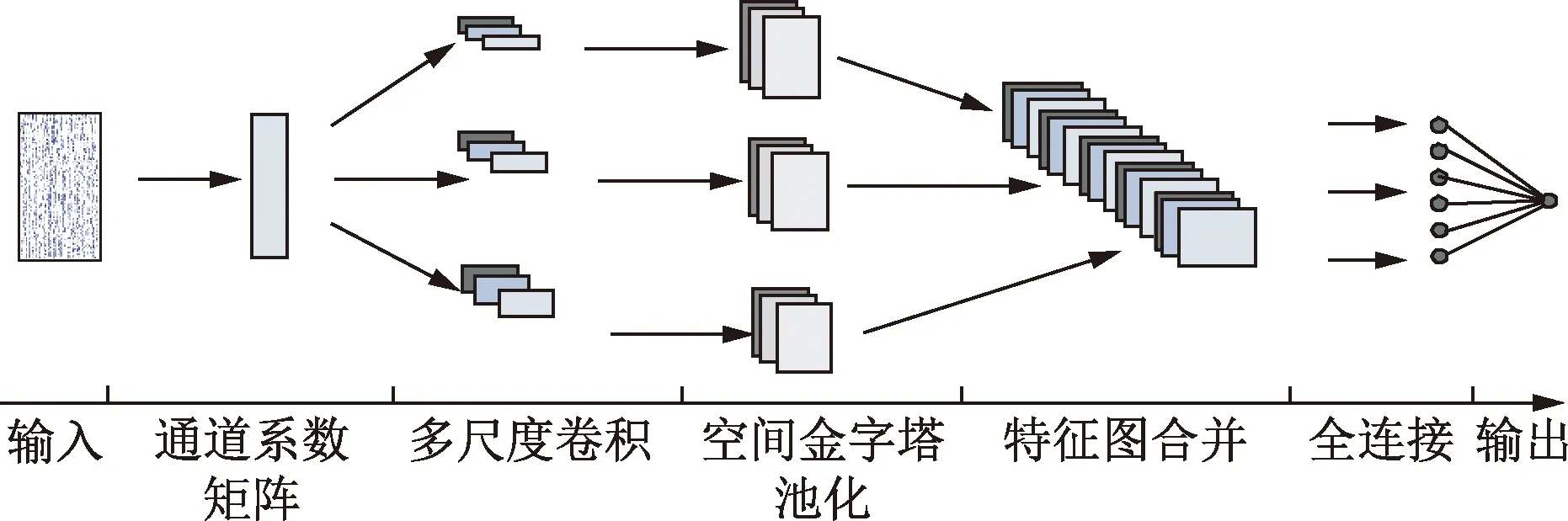
图3 多尺度卷积核CNN网络结构图Fig.3 Multi-scale convolution kernel CNN network structure

3 实验与结果分析

3.1 网络模型参数选择

为了找到一组最佳的网络模型参数，选取渭南和那曲两个数据集分别做单尺度和多尺度的二分类对比实验。卷积核尺寸大小为3～32，激活函数使用ReLu函数，学习率设置为0.001，步长设置为1，padding层为设置为0，池化层采用空间金字塔池化法[19]，每个batch处理128个脑电数字矩阵，训练次数为50个epoch。

首先验证多尺度卷积核CNN的有效性。分别设置卷积层为单一尺度卷积核[6]、[12]、[25]，设置多尺度卷积核尺寸为[6,12,25]，即卷积层循环使用尺寸为[6]、[12]、[25]三种大小的卷积核，网络的其他参数设置不变。图4为50个epoch中测试集上单尺度与多尺度的实验结果图。图4中四条曲线准确率从高到低依次为多尺度[6,12,25],单尺度[25]、[12]和[6]。单尺度上准确率随着卷积核尺寸的增加而增加，但提高的幅度不是很大，而多尺度的分类准确率明显高于其他三个单尺度，分类准确率比单尺度分类最好的高约8%，这是由于多尺度卷积核尺寸组合由小到大，可以从不同的感受野提取信号的特征，提取的信息特征更细致，所以效果更好。

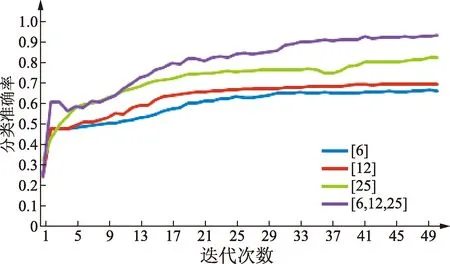
图4 单尺度与多尺度准确率对比Fig.4 Single-scale and multi-scale accuracy comparison

其次寻找一组最佳的多尺度卷积核组。选取3个尺寸均比较小卷积核组成多尺度[3,6,9]，3个尺寸均中等大小的组成多尺度[10,12,15]，3个尺寸均较大的组成[16,20,25]三种多尺度CNN模型与由尺寸相对较小、中等和较大的卷积核组成的[6,12,25]多尺度CNN模型在其他参数设置不变的情况下做对比。图5为多尺度与多尺度准确率对比结果。图5中分类准确率最高的紫色线条为尺度组合为[6,12,25]的多尺度CNN模型，虽然尺寸较大的组合[16,20,25]分类准确率也较高，但是与[6,12,25]这一组还有约3%的差距。这是由于[6,12,25]这组卷积核尺寸差异较大，可以更全面地提取到数据的特征，而其他三组卷积核尺寸差异较小，提取到的特征相对单一，准确率较低。

图5 多尺度与多尺度准确率对比Fig.5 Multi-scale and multi-scale accuracy comparison

根据以上两组对比，确定网络模型中卷积核的尺寸组合为[6,12,25]，网络模型的参数选择如表1所示。

表1 网络模型参数Table 1 Network model parameter

3.2 高原脑电分类实验

确定好参数后，用选定参数的脑电模型对不同海拔脑电数据做二分类、三分类和四分类实验，分类的准确率在训练集和测试集上的结果以及损失值分别如图6所示。

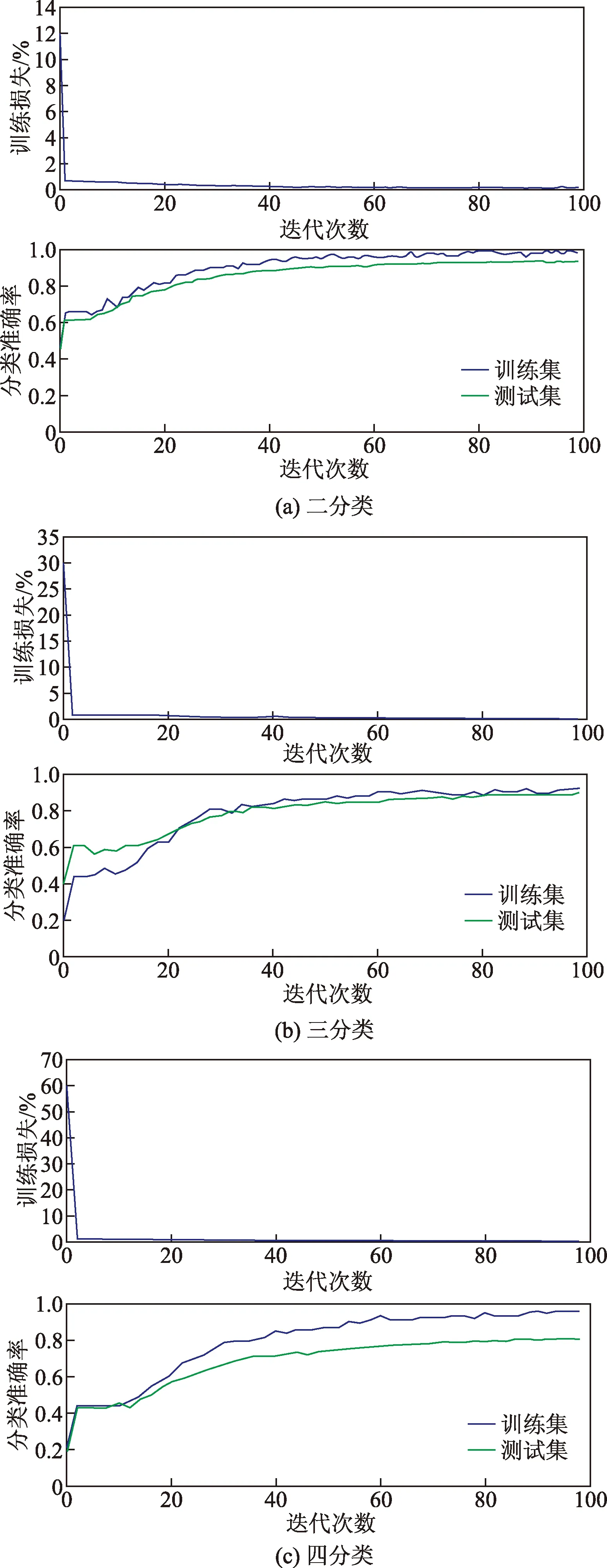
图6 二、三、四分类准确率与损失值结果Fig.6 Each classification accuracy and loss value results

由图6可知，二分类在训练集上最高可以达到98.43%，测试集上可以达到93.59%；三分类任务中训练集最高为92.87%，测试集上为90.17%；四分类任务中训练集准确率最高为91.40%，测试集为81.15%。二分类和三分类任务中，训练集和测试集分类准确率相差不大，而在四分类任务中训练集准确率可以达到91%，而在测试集上只有81%，是因为二分类、三分类任务中使用的数据集为渭南、那曲和林芝，其数据量较多，而拉萨的数据量较少，和其他三个海拔的数据量相差明显，所以在四分类时导致测试集上效果不理想。

4 结论

以CNN网络为原型，通过改造CNN的卷积层优化网络结构，并在输入数据前加系数矩阵，通过不同海拔脑电数据的多分类实验验证了所提出的脑电分类模型的优越性。在高原脑电二分类的对比中多卷积核卷积神经网络模型的准确率提高了约8个百分点，在三分类和四分类的实验中准确率达到了92.87%和81.15%。所以提出的脑电分类模型有一定的参考价值。