固结磨料研磨单晶蓝宝石亚表面损伤的预测
2020-06-30王建彬马睿江本赤王刚李军朱永伟
王建彬,马睿,江本赤,王刚,李军,朱永伟
固结磨料研磨单晶蓝宝石亚表面损伤的预测
王建彬1,2,马睿1,江本赤1,王刚1,李军2,朱永伟2
(1.安徽工程大学 机械与汽车工程学院,安徽 芜湖 241000;2.南京航空航天大学 机电学院 江苏省精密与微细制造技术重点试验室,南京 210016)
为了准确预测工件亚表面损伤,合理确定材料去除量,优化固结磨料研磨单晶蓝宝石的工艺参数。针对固结磨料研磨特点和单晶蓝宝石特性,采用离散元模拟技术,建立单晶蓝宝石材料的离散元模型,仿真固结磨料对材料研磨的动态过程,分析载荷作用下材料单元颗粒间裂纹的产生和扩展规律,研究磨粒切入深度对亚表面损伤的影响,预测固结磨料研磨单晶蓝宝石亚表面裂纹的数量和深度,并借助化学腐蚀法验证预测结果。采用粒度分别为W14、W28、W50、W65的金刚石固结磨料垫,其对应的研磨单晶蓝宝石亚表面损伤层深度预测值分别为3.75、5.28、7.62、10.92 μm,预测的裂纹数量分别为199、236、526、981条,对应的实验实测值分别为3.79、5.88、8.76、11.44 μm。固结磨料垫中的磨料粒径越大,单晶蓝宝石亚表面损伤层的深度越大,裂纹数量越密集。对比发现腐蚀实验的实测值和理论预测值基本一致,验证了预测结果模型的正确性。采用离散元法可以快速有效地预测固结磨料研磨单晶蓝宝石亚表面损伤层的裂纹数量和深度,为研磨工艺参数的优化和后续抛光工艺参数的制定提供指导。
单晶蓝宝石;亚表面损伤;离散元法;固结磨料;研磨;化学腐蚀法
单晶蓝宝石因具有较高的硬度、优异的透光性及良好的耐磨和耐腐蚀性能,而被广泛应用于固态照明LED衬底、智能电子触摸屏及军事红外探测窗口等[1-4]。随着单晶蓝宝石应用领域的不断扩大,对其表面/亚表面质量的加工要求也越来越高。但由于单晶蓝宝石的硬脆特性,导致其加工难度大、加工工艺复杂,尤其是作为最终工序的抛光,其去除效率和材料表层的整体去除量均较小,很难在短时间内获得优质的加工表面。因此,作为前道工序的研磨成为决定后续抛光时间和成本的关键工序[5-7],开展针对单晶蓝宝石研磨加工的亚表面损伤研究,对于合理确定研磨去除量、优化研磨工艺参数、高效获得超光滑表面具有重要意义。
研磨后单晶蓝宝石工件的亚表面损伤一直是国内外学者关注的重点。依据检测工件是否受到破坏,可把单晶蓝宝石亚表面损伤的检测分为破坏性检测和非破坏性检测。其中,利用高温KOH与单晶蓝宝石的化学反应测算腐蚀速率的高温腐蚀法[6-8],以及通过调节腐蚀液配比和温度的低温湿法刻蚀均都属于破坏性检测[9]。该方法虽然能够精确地检测出蓝宝石亚表面损伤层深度,但由于腐蚀液的破坏作用,试样的亚表面损伤特征不能完全反映出来,且检测时间长,检测后样件难以继续使用。而利用光学原理借助TEM、X射线衍射和拉曼光谱技术呈现单晶蓝宝石亚表面损伤的非破坏性检测[10-11],检测结果过分依赖于操作者,且存在检测系统成本高、测量精度低、测量结果不直观等缺陷。综上所述,目前对单晶蓝宝石亚表面损伤研究较多地关注于事后的深度检测,而对于亚表面损伤的产生机制及事前的深度预测还很少涉及。
形成于20世纪70年代的离散元法,其原理是以颗粒集合系统为载体模拟非线性作用下的材料流动和混合,解决不连续离散介质的数值仿真。该方法通过一系列模拟实验建立微观参数与材料宏观力学性能间的映射关系,将空间离散转换为离散单元阵,建立仿真样本[12]。离散元法中空间颗粒离散单元间的连接和流动特性与研磨加工中材料分子颗粒受磨粒作用而产生的滑移较为类似,故近年来有专家尝试利用离散元法分析硅片、石英玻璃、镁铝尖晶石等材料加工时的裂纹特性[13-15]。由于离散元法在研磨加工中的应用研究还处于起步阶段,尤其是在固结磨料研磨单晶蓝宝石的亚表面预测方面尚未见文献报道。
本文针对单晶蓝宝石的材料特性,首先,利用离散元软件建立单晶蓝宝石的二维离散元模型,模拟金刚石固结磨料研磨时的磨粒运动过程,分析离散球形颗粒单元间裂纹的产生和扩展规律。依据固结磨料研磨单晶蓝宝石的磨粒切入深度,研究不同粒度的金刚石固结磨料对单晶蓝宝石的亚表面损伤规律,预测亚表面损伤的裂纹数量和深度,揭示亚表面损伤的产生机制;其次,采用化学腐蚀法测量固结磨料研磨单晶蓝宝石的亚表面损伤层深度;最后,对比离散元模型的仿真结果和实验测得值,确定合理的材料去除深度,为单晶蓝宝石研磨工艺参数的制定提供参考。
1 单晶蓝宝石离散元模型的构建
1.1 离散元模型的建立
单晶蓝宝石是由氧原子和铝原子组成的配位型氧化物晶体,晶体结构中的原子类似于球体,通过共价键形式连接,因此可以将单晶蓝宝石原子假定为离散的球形单元颗粒体。采用离散元软件PFC建立二维离散元模型如图1所示,图中离散的球形颗粒为独立刚性单元体,颗粒间呈现紧密排列,并在一定强度连接键的约束下形成集合体。为了使理论模型参数与实际宏观力学参数相匹配,对离散元模型进行虚拟的单轴压缩、巴西圆盘拉伸、单边切口校核。校核后的模型参数与实测力学参数对比如表1所示[16-18]。由表1可知,离散元模型中的力学参数指标和实测参考值基本一致,故该模型具有可靠的理论基础。

图1 单晶蓝宝石的二维离散元模型
表1 模型校核参数与实测力学性能参数对比

Tab.1 Comparison between model checking parameters and measured mechanical properties
1.2 亚表面裂纹的形成
离散的刚性颗粒单元集合体受到外加载荷作用时,颗粒单元间连接键的键能因接触力作用而减弱,距离接触力作用点越近,键能的减弱程度越大,反之则越小。颗粒单元间连接键的连接强度因键能的改变而变化,在接触点下方的颗粒单元体出现滑移,连接键呈现出类似于微裂纹的状态,如图2a所示。当接触力作用足够大时,距离作用点最近的颗粒单元间连接键断裂,部分颗粒单元脱离集合体,如图2b所示。
a 微裂纹的形成
b 颗粒分离
图2 微裂纹的形成与颗粒分离
Fig.2 Formation of microcracks and particle separation: (a) formation of microcracks; (b) particle separation
在固结磨料研磨单晶蓝宝石过程中,材料表层受到接触磨粒的机械作用,在接触点下方形成一定数量的亚表面裂纹。实际加工中,磨粒与材料间接触力的大小通过磨粒的切入深度来表示,故单晶蓝宝石的亚表面损伤与磨粒的切入深度直接相关[6,15]。固结磨料研磨单晶蓝宝石的磨粒切入深度除了和磨料粒径尺寸有关外,还受制于固结磨料垫的结构。为了简化模型,假设由树脂基体包裹的磨粒为球形刚体,均布在固结磨料垫表面,其在高度方向的出露也是均匀的,则固结磨料垫表面理论磨粒个数0和单颗磨粒对单晶蓝宝石样件的最大切深分别为[6]:



式中:0为工件的面积,0为固结垫凸起面积与总面积的比值,为磨粒的体积浓度,为研磨压力,s为单晶蓝宝石样件的屈服强度,max为磨粒的最大出露高度取粒径的1/3,为磨粒直径,为实际接触的磨粒组数。
依据固结磨料垫特性和研磨压力等工艺参数,利用公式(1)—(3)可获得不同粒径金刚石固结磨料对单晶蓝宝石的切入深度(表2),把切深代入离散元模型即可对单晶蓝宝石亚表面损伤层裂纹进行模拟。
表2 不同粒径固结磨料垫对应单晶蓝宝石的最大切深

Tab.2 Maximum cutting depth of sapphire under fixed pads with different diameter
2 实验
2.1 样件的制备
实验采用的样件为直径50.8 mm、厚度0.5 mm左右的C向单晶蓝宝石片。在腐蚀实验前,利用金刚石固结磨料垫研磨加工样件,固结磨料垫中的金刚石粒径分别为W65、W50、W28、W14。研磨时采用相同的研磨液和工艺参数,其中研磨液为去离子水+ 0.3%OP-10乳化剂,研磨工艺参数如表3所示。
表3 固结磨料研磨蓝宝石工艺参数

Tab.3 Lapping process parameters of lapping sapphire with fixed abrasive
2.2 亚表面损伤层深度的检测
采用箱式电阻炉加热固态KOH至300 ℃,使其处于高温熔融状态,把不同固结磨料垫研磨后的单晶蓝宝石样件超声清洗干净,放入熔融态高温KOH进行腐蚀。腐蚀后待样件冷却至室温,用去离子水冲洗5 min,并用0.5%稀盐酸浸泡20 min,再用去离子水清洗5 min,用无水乙醇超声清洗20 min,电吹风吹干。采用精密天平FA1604(220 g/0.1 mg)分别计量腐蚀前后的质量变化,以5次测量的均值作为测量结果,每次腐蚀时间为10 min。由于样件的厚度相对于直径尺寸,其数值较小,故厚度方向腐蚀前后的质量变化可忽略不计,假定单晶蓝宝石样件的密度恒定且双面被均匀腐蚀,则可依据公式(4)测算腐蚀深度Δ式中和分别表示单晶蓝宝石腐蚀前的厚度和质量,m和m-1分别为第次腐蚀前后的质量。腐蚀速率和腐蚀加速度分别为Δ/(2)和Δ,Δ为时间腐蚀前后的腐蚀速度差。实验采用金相显微镜ZL200JT观测腐蚀前后单晶蓝宝石样件的表面形貌。

3 结果与讨论
3.1 不同粒径下的亚表面损伤深度仿真
仿真过程中,利用表2中不同粒径金刚石固结磨料垫研磨单晶蓝宝石样件的最大切深,假设磨粒以20 m/s的速度在工件表面作直线运动,设定相同的时步为80 000步,利用离散元模型即可仿真出相同工艺参数下,不同粒径单颗金刚石磨粒研磨单晶蓝宝石过程中的亚表面裂纹分布和扩散深度如图3所示。随着金刚石粒径增大,磨粒切入深度增加,模型中裂纹分布深度和密集程度不断加大。当磨料粒径为W14时,磨粒的切入深度相对较小,亚表面裂纹的分布深度仅在颗粒单元体的1~2层,仿真得出亚表面损伤深度为3.75 μm,裂纹数量为199条。而当磨料粒径增大到W65时,由图3d中可以看出亚表面裂纹的分布深度和密集程度明显增大,其数值分别为10.92 μm和981条。
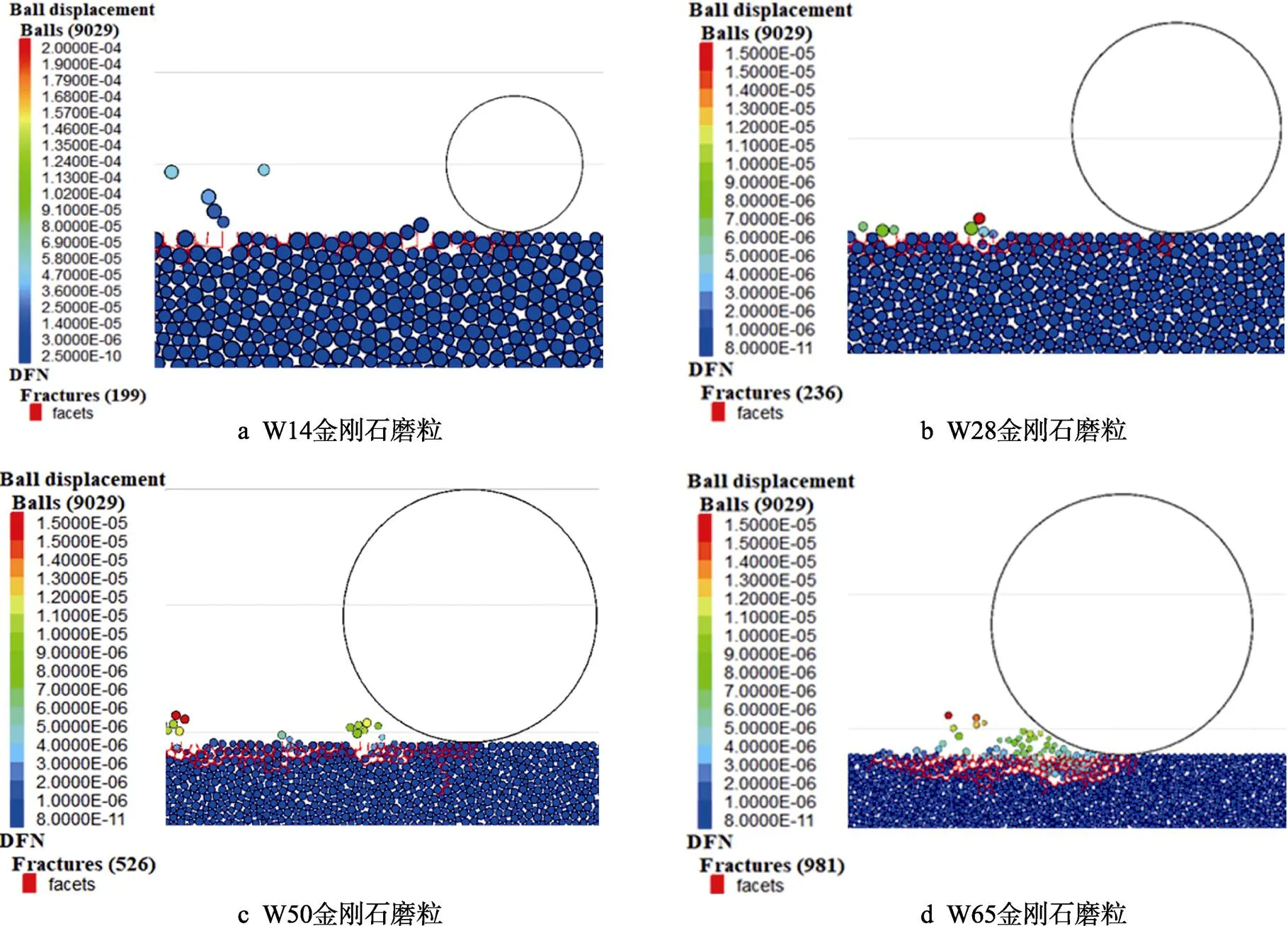
图3 单颗磨粒仿真研磨后亚表面损伤模型图
从仿真模型得出的磨粒粒径与亚表面损伤深度及裂纹数量关系如图4所示。亚表面损伤深度随着磨料粒径的变大而加深,裂纹数量随着磨料粒径的变大而增多。这可能是由于粒径较小的磨粒切入单晶蓝宝石样件表层的深度较浅,不易造成表层单元颗粒间连接健的破坏,其亚表面损伤的深度和数量相对较小。而当采用W65的金刚石磨料时,磨粒的切入深度最大,磨粒接触处的作用力最大,工件表层材料颗粒体由于受到较大的法向载荷作用,深度方向形成密致交错的微裂纹,颗粒体间的连接键强度减弱,并扩展至一定深度。同时,由于磨料与工件相对运动产生的剪切应力加剧了亚表面裂纹的扩展,并使表层部分颗粒体脱离,其过程与磨粒加工宏观呈现的刮擦、耕犁和切削相对应。

图4 磨粒粒径与亚表面损伤深度及裂纹数量
3.2 不同粒径下的亚表面损伤实验研究
利用化学腐蚀法测得不同粒径下固结磨料垫研磨单晶蓝宝石的表面/亚表面腐蚀速度和加速度曲线如图5所示。随着腐蚀时间的增加,不同粒径下固结磨料垫研磨后,单晶蓝宝石腐蚀速度和加速度的变化趋势基本一致,其数值不断减小,经过一定的腐蚀时间后,工件的腐蚀速度基本不变,腐蚀的加速度趋近于零。这主要是因为腐蚀初期,样件表面/亚表面损伤层较大,裂纹的深度和数量较多,化学腐蚀液较易渗入,从而与更大面积的表层原子接触发生化学腐蚀作用,导致较高的腐蚀速率,而随着腐蚀时间的增加,样件表面/亚表面被损伤的部分逐渐被腐蚀掉,腐蚀速率必然趋缓[6,19]。当样件的亚表面损伤被完全去除后,样件的基体层与腐蚀液接触,腐蚀速率保持恒定且与腐蚀时间无关。
进一步分析不同粒径作用下单晶蓝宝石腐蚀前后的表面形貌如图6所示,其中图6a—d为腐蚀前的表面形貌,可以看出腐蚀前的样件表面布满不规则凹坑。随着磨料粒径的增大,其对应样件表面逐渐出现较为明显的划痕,粒径为W65作用后的样件表面划痕最为显著。图6e—h分别为样件腐蚀50、40、30、20 min后的表面形貌,可以看出腐蚀后的样件表面均呈现出较为规则的形状,且形状基本类似,从而推断样件的亚表面损伤层已经完全被腐蚀液去除。依据不同样件腐蚀形貌呈现规则形状所需的腐蚀时间,再次分析图5可知,当腐蚀速率基本恒定、腐蚀加速度基本为零时,腐蚀速率曲线在此时出现拐点。假定单晶蓝宝石密度不变,则可由腐蚀前后的质量差和累计腐蚀时间,推断出其亚表面损伤层深度。故当磨料粒径分别为W65、W50、W28、W14时,其对应的样件亚表面损伤层深度分别为11.44、8.76、5.88、3.79 μm。
当磨料粒径相对较大时,固结磨料垫上凸起的金刚石磨粒与单晶蓝宝石样件表面接触,由于磨料颗粒的非均匀性,导致单位面积上的接触压强随粒径的增大而增大,易形成较大切深,加剧亚表面损伤,宏观上在样件表面呈现出明显的划痕。而随着磨料粒径的减小,在树脂中包裹的金刚石磨粒不易出露,导致树脂基体承担部分研磨压力,一定程度上减缓了磨粒的切入深度,形成较小的亚表面损伤。也可以进一步解释图3中腐蚀速率曲线斜率的变化,大粒径作用下导致单晶蓝宝石样件亚表面损伤较大,故其腐蚀速率的曲线斜率变化较大,反之则腐蚀速率的曲线斜率变化较小。

图6 不同粒径作用下单晶蓝宝石腐蚀前后的形貌
3.3 亚表面损伤的仿真预测与实验对比分析
采用不同粒度的金刚石固结磨料垫研磨单晶蓝宝石样件,加工后样件亚表面损伤的实验结果和仿真预测对比如图7所示。可以看出,在仿真预测与实际实验过程中,磨粒粒径从W14、W28、W50增大到W65时,随着磨粒切入深度的增加,工件表面/亚表面的裂纹深度和密度也相应增加,且仿真预测结果和实验的变化趋势基本相同,说明通过建立离散元模型可以较为准确地预测固结磨料研磨单晶蓝宝石样件的亚表面损伤层深度。
进一步观察发现仿真预测与实际实验结果之间也存在一定的差别,表现为实验结果普遍大于仿真模型的预测。造成这一现象的主要原因可能是:首先,仿真预测模型中材料假设为均匀的理想球状密排堆积,而实际单晶蓝宝石的原子大小和间距均有差异,连结原子的键长和键能也不尽相同,故磨粒压入时若以均匀密排的仿真模型预测切入深度,必然与实际情况有所出入;其次,仿真模型中,为了便于计算仅假设磨粒大小均匀且为匀速直线运动,简化了实际加工的复杂性;再次,固结磨料垫中的磨粒大小具有一定范围,加工时部分颗粒较大的磨粒易脱落,在工件表面间以一定的速度进行滚轧,必然会造成较大的亚表面损伤;最后,采用化学腐蚀法仅以质量变化测算亚表面损伤,忽略了蓝宝石样件表面/亚表面损伤的非均匀性和厚度方向的腐蚀量,故腐蚀法测量的实验结果必然大于仿真预测结果。
4 结论
1)采用离散元法仿真固结磨料研磨单晶蓝宝石的力学行为,预测样件亚表面裂纹数量和损伤层深度,当磨料粒径分别为W14、W28、W50、W65时,其对应的裂纹数量分别为199条、236条、526条、981条,亚表面损伤层深度分别为3.75、5.28、7.62、10.92 μm,亚表面裂纹数量和损伤层深度均随着磨料粒径的增大而增加。
2)采用化学腐蚀法对研磨后的单晶蓝宝石样件进行亚表面损伤检测实验,磨料粒径分别为W14、W28、W50、W65的固结磨料作用下的亚表面损伤层深度分别为3.79、5.88、8.76、11.44 μm。
3)磨料粒径对固结磨料研磨单晶蓝宝石亚表面裂纹的密集程度和损伤层深度影响显著,控制磨料粒径是改善亚表面损伤的有效途径。
[1] XU Yong-chao, LU Jing, XU Xi-peng. Study on planarization machining of sapphire wafer with soft-hard mixed abrasive through mechanical chemical polishing[J]. Applied surface science, 2016, 389: 713-720.
[2] KHATTAK C P, SHETTY R, SCHWERDTFEGER C R, et al. World's largest sapphire for many applications[J]. Journal of crystal growth, 2016, 452: 44-48.
[3] 张荣实. 红外窗口整流罩技术新进展[J]. 红外与激光工程, 2007, 36(9): 114-118. ZHANG Rong-shi. Recent advances in infrared window and dome technologies[J]. Infrared and laser engineering, 2007, 36(9): 114-118.
[4] 钟敏, 袁任江, 李小兵, 等. 磨粒和抛光垫特性对蓝宝石超声化学机械抛光的影响[J]. 中国表面工程, 2018, 31(6): 125-132. ZHONG Min, YUAN Ren-jiang, LI Xiao-bing, et al. Effects of abrasive particles and pads’ characteristics on ultrasonic assisted chemical mechanical polishing for sapphire[J]. China surface engineering, 2018, 31(6): 125-132.
[5] LEE H C, MEISSNER H E. Characterization of AFB (R) sapphire single crystal composites for infrared window application[J]. Proceedings of SPIE, 2007, 6545: 1-8.
[6] 王建彬. 固结磨料研磨蓝宝石工件的材料去除机理及工艺研究[D]. 南京: 南京航空航天大学, 2015. WANG Jian-bin. Material removal mechanism and process research of lapping sapphire by fixed abrasive[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2015.
[7] 孟庆平. 蓝宝石高效超精密磨削技术及损伤检测研究[D]. 大连: 大连理工大学, 2009. MENG Qing-ping. Study on high efficiency and ultra-precision grinding process and machining damage of sapphire[D]. Dalian: Dalian University of Technology, 2009.
[8] 谢春, 汪家林, 唐慧丽. 碳化硼研磨后蓝宝石晶体的亚表面损伤[J]. 光学精密工程, 2017, 25(12): 3070-3078. XIE Chun, WANG Jia-lin, TANG Hui-li. Subsurface damage of sapphire crystal after lapping with boron carbide abrasives[J]. Optics and precision engineering, 2017, 25(12): 3070-3078.
[9] KUMA P, LEE J, LEE G, et al. Low temperature wet etching to reveal sub-surface damage in sapphire substrates[J]. Applied surface science, 2013, 69(1-4): 277-290.
[10] BLACK D R, POLVANI R S, BRAUN L M, et al. Detection of subsurface damage: studies in sapphire[C]//Aero sense' 97. Florida: Window and dome technologies and materials V, 1997: 102-114.
[11] WANG Jian-bin, WU Ke, MAEZAKI T, et al. Development of binder-free CMG abrasive pellet and finishing performance on mono-crystal sapphire[J]. Precision engineering, 2020, 62: 40-46.
[12] STRACK O D L, CUNDALL P A. The distinct element method as a tool for research in granular media[M]. Minnesota: University of Minnesota, 1978.
[13] RANDI J A, LAMBROPOULOS J C, JACOBS S D. Subsurface damage in some single crystalline optical materials[J]. Applied optics, 2005, 44(12): 2241-2249.
[14] 谭援强, 杨冬民, 李才, 等. 单晶硅加工裂纹的离散元仿真研究[J]. 中国机械工程, 2008, 19(21): 2545-2548. TAN Yuan-qiang, YANG Dong-min, LI Cai, et al. Discrete element method simulation of cracks in monocrystalline silicon machining process[J]. China mechanical engineering, 2008, 19(21): 2545-2548.
[15] 朱永伟, 李信路, 王占奎, 等. 光学硬脆材料固结磨料研磨中的亚表面损伤层预测[J]. 光学精密工程, 2017, 25(2): 367-374. Zhu Yong-wei, Li Xin-lu, Wang Zhan-kui, et al. Subsurface damage prediction for optical hard brittle material in fixed abrasive lapping[J]. Optics and precision engineering, 2017, 25(2): 367-374.
[16] YANG B, JIAO Y, LEI S. A study on the effects of microparameters on micro properties for specimens created by bonded particles[J]. Engineering computations, 2006, 23(6): 607-631.
[17] 蒋明镜, 方威, 司马军. 模拟岩石的平行粘结模型微观参数标定[J]. 山东大学学报(工学版), 2015, 45(4): 50-56.JIANG Ming-jing, FANG Wei, SIMA Jun. Calibration of micro-parameters of parallel bonded model for rocks[J]. Journal of Shandong University of Technology, 2015, 45(4): 50-56.
[18] 尹小涛, 李春光, 王水林, 等. 岩土材料细观、宏观强度参数的关系研究[J]. 固体力学学报, 2011, 32(S1): 343-351. YIN Xiao-tao, LI Chun-guang, WANG Shui-lin, et al. Study on relationship between micro-parameters and macro- parameters of rock and sold material[J]. Chinese journal of sold mechanics, 2011, 32(S1): 343-351.
[19] 李军, 王健杰, 郭太煜, 等. 侧面逐层抛光腐蚀法研究亚表面损伤[J]. 表面技术, 2019, 48(8): 309-315. LI Jun, WANG Jian-jie, GUO Tai-yu, et al. Subsurface damage studied by side layer-by-layer polishing and etching method[J]. Surface technology, 2019, 48(8): 309-315.
Prediction of Subsurface Damage for Fixed Abrasive Lapping Single Crystal Sapphire
1,2,1,1,1,2,2
(1.School of Mechanical and Automobile Engineering , Anhui Polytechnic University, Wuhu 241000, China; 2. Jiangsu Key Laboratory of Precision and Microfabrication Technology, School of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
The work aims to accurately predict the subsurface damage of the workpiece, reasonably determine the material removal amount, and optimize the process parameters of the single-crystal sapphire with the fixed abrasive. According to the lapping characteristics of fixed abrasives and the properties of single crystal sapphire, the discrete element model of single crystal sapphire was established by discrete element method, the dynamic process of lapping the material by fixed abrasive was simulated, the generation and propagation of cracks between element particles under load were analyzed, the effect of cut depth of abrasive grains on subsurface damage was studied, the number and depth of subsurface cracks of single crystal sapphire lapped by fixed abrasives were predicted, and the prediction results were verified by chemical corrosion method. The results indicated that with the fixed abrasive pads with particle sizes of W14, W28, W50 and W65, the corresponding predicted depth of the lapped sapphire subsurface damage layers was 3.75 μm, 5.28 μm, 7.62 μm and 10.92 μm; the predicted number of cracks was 199, 236, 526 and 981; and the corresponding experimental values were 3.79 μm, 5.88 μm, 8.76 μm, and 11.44 μm, respectively. As the abrasive particle size in the fixed abrasive pad increased, the depth of the single crystal sapphire subsurface damage layer and the number of cracks also increased. The comparison showed that the measured values and predicted values were basically consistent, and the correctness of the prediction results was verified. Therefore, the discrete element method can quickly and effectively predict the number and depth of cracks in the sapphire subsurface damage layer of the fixed abrasive, and provide guidance for the optimization of the lapping process parameters and the formulation of subsequent polishing process parameters.
single crystal sapphire; subsurface damage; discrete element method; fixed abrasive; lapping; chemical etching
2019-12-31;
2020-02-27
WANG Jian-bin (1982—), Male, Doctor, Associate professor, Research focus: ultra-precision machining technology.
李军(1979—),男,博士,副教授,主要研究方向为超精密加工技术。邮箱:junli@nuaa.edu.cn
Corresponding author:LI Jun (1979—), Male, Doctor, Associate professor, Research focus: ultra-precision machining technology. E-mail: junli@nuaa.edu.cn
王建彬, 马睿, 江本赤, 等. 固结磨料研磨单晶蓝宝石亚表面损伤的预测[J]. 表面技术, 2020, 49(6): 345-351.
TG365.28
A
1001-3660(2020)06-0345-07
10.16490/j.cnki.issn.1001-3660.2020.06.042
2019-12-31;
2020-02-27
安徽省高校优秀青年人才支持计划重点项目(gxyqZD2019051);安徽省自然科学基金资助项目(1708085QE127);校国家基金预研项目(2017yyzr06);安徽省人才项目(Z175050020001);安徽工程大学2018年度中青年拔尖人才培养计划;南京航空航天大学江苏省精密与微细制造技术重点实验室开放基金
Fund:Supported by the Key Project of Excellent Young Talents Support Program of Anhui Province (gxyqZD2019051); Funded by the Natural Science Foundation of Anhui Province (1708085QE127); National Fund Pre-research Project of the University (2017yyzr06); Talent Project of Anhui Province (Z175050020001); Anhui Engineering University's 2018 Young Talent Training Program; Nanjing Aerospace University Jiangsu Key Laboratory of Precision and Micro Manufacturing Technology Open Fund
王建彬(1982—),男,博士,副教授,主要研究方向为超精密加工技术。
WANG Jian-bin, MA Rui, JIANG Ben-chi, et al. Prediction of subsurface damage for fixed abrasive lapping single crystal sapphire[J]. Surface technology, 2020, 49(6): 345-351.
