基于Stoney公式适用性分析——取向硅钢绝缘涂层张应力的计算
2020-06-30刘兆月司良英马家骥黎先浩杨平滕仁昊王现辉
刘兆月,司良英,马家骥,黎先浩,杨平,滕仁昊,王现辉
基于Stoney公式适用性分析——取向硅钢绝缘涂层张应力的计算
刘兆月1,2,司良英2,马家骥3,黎先浩2,杨平1,滕仁昊2,王现辉2
(1.北京科技大学 材料科学与工程学院,北京 100083;2.首钢智新迁安电磁材料有限公司,河北 迁安 064404;3.北京首钢股份有限公司,河北 迁安 064404)
改善涂层张应力状态,进而提升取向硅钢的电磁性能。用扫描电镜、辉光光谱仪分析了添加磷酸盐的胶体二氧化硅绝缘涂层的厚度和微观结构,采用静态拉伸试验得到了取向硅钢沿不同位向的力学特性。在此基础上,根据取向硅钢各向异性的特点和绝缘涂层的实际状态,用Stoney公式对取向硅钢涂层应力的适用性进行了讨论。取向硅钢的各向异性不满足Stoney公式的适用条件,实际测试的取向硅钢的力学性能结果表明,取向硅钢符合正交对称各向异性材料的一般规律,据此给出了涂层对取向硅钢产生的张应力的计算公式,利用该公式对不同涂覆工艺条件下的胶体二氧化硅绝缘涂层的张应力进行了计算,涂层厚度在1~2 μm范围内,双面张应力的计算值为4~11 MPa。文中张应力的计算公式不仅适用于取向硅钢,同样适用于其他基体为各向异性的类似情况。通过张应力的计算可知,涂层厚度与张应力呈正相关,张应力的增大将会促使取向硅钢的铁损降低。因此,开发大张力的绝缘涂层,是进一步改善取向硅钢磁性能的有效途径之一。
取向硅钢;绝缘涂层;张应力;Stoney公式;各向异性
作为电力和电子行业不可或缺的一种重要的软磁材料,取向硅钢广泛地应用在变压器等电力设施中。因具备锋锐的Goss({110}<001>)织构,取向硅钢具有高磁感、低铁损的优势[1-2]。随着节能降耗、淘汰落后产能的需求不断提升,降低取向硅钢的铁损已经成为工业生产的核心目标之一。为达到这一目的,不仅需要采用合理的工艺参数优化材料本身的组织特性,同时也可以沿取向硅钢轧向施加一定的张应力来进一步降低铁损[3-8]。在实际生产过程中,通过各种方式使取向硅钢表面覆盖应力层(硅酸镁底层、应力绝缘涂层及其他涂层)就可以实现施加张应力的目的,取向硅钢表面的应力绝缘涂层不仅能够有效降低铁损,还可以改善耐蚀性、提高可加工性及降低变压器的噪音,从而提升产品的综合使用性能[9-15]。分析涂层对基体的张应力,有助于指导现场工艺优化、提升产品性能和开发新型涂层。因此,需要采用恰当的方法来测试硅钢基体受到来自涂层的张应力。
相对于其他测试方法,曲率法测量范围广、方法简单,对基体及涂层的种类和状态的要求较低,避免了因涂层局部缺陷引起的测量偏差大等问题[16]。1909年,Stoney[17]推导并提出了用于曲率法测量涂覆层残余应力的计算公式,并用此公式计算了电沉积镍薄膜的残余应力。该公式自提出以来得到了广泛应用,已有许多学者以此为基础,计算了包括半导体、陶瓷、电解沉积金属及氧化膜等在内的涂(覆)层残余应力数据[18-23]。曾有学者采用Stoney公式对陶瓷膜对基体的张应力进行分析[15],得到了涂层的张应力数据。然而,Stoney公式是否适用于取向硅钢涂层尚需细致分析。另外,对绝缘涂层产生的应力进行计算和分析的相关研究报道较少。
本文以Stoney公式[17-18]为基础,结合取向硅钢及涂层特性,对公式进行了适用性的讨论,并给出了适用于取向硅钢的计算公式。以此为基础,对取向硅钢绝缘涂层的应力进行了分析,简要讨论了张应力与涂层厚度之间的关系,并分析了张应力对铁损的影响。
1 试验
1.1 样品制备
本文的研究对象为0.27 mm厚度的3%Si-Fe高磁感取向硅钢,经过热轧、冷轧、脱碳渗氮、涂覆氧化镁及高温退火后,发生二次再结晶,在表面生成一层硅酸镁底层,然后涂覆应力绝缘涂层,最终获得表面状态良好的高磁感取向硅钢。绝缘涂层以胶体SiO2为主,并加入了磷酸盐等无机盐类。分别采用5组不同涂布量参数,在同样的烧结条件下,在样品表面涂覆了应力绝缘涂层。
1.2 曲率法测试原理
采用曲率法进行张应力测试,样品仅存在一侧涂层的情况下获得样品弯曲的曲率。取尺寸为30 mm× 300 mm的样品(长边方向即为应力测试方向,本文为轧向),单侧存在绝缘涂层时发生弯曲,此时样品轧面可以近似看作圆柱侧面的一部分,长边则可以认为是圆柱底面圆的部分弧长。通过简单的几何学就能计算出这个底面圆的半径,可以得到所需的曲率半径
1.3 性能测试及组织分析
为保证准确性,以下测量样品均取自待测样品周围部位。
1)利用静态拉伸试验实测无绝缘涂层的样品(表面存在硅酸镁底层)的弹性模量和泊松比数据。
2)利用扫描电镜对取向硅钢表面涂层的形貌进行分析。
3)利用辉光光谱仪测量绝缘涂层的厚度,其分析区域大小是直径为3 mm的圆,相对于微观方法更具代表性。由于取向硅钢还存在硅酸镁底层,涂层状态较为复杂,以成品取向硅钢的分析结果为例(见图1)对分析方法进行说明:在距离表面1.3 μm处,Mg元素和Si元素含量发生明显变化,绝缘涂层中的其他元素逐渐消失,则可认为此处是硅酸镁底层与绝缘涂层的交界位置,即本例中绝缘涂层的厚度大约为1.3 μm。
4)利用爱泼斯坦方圈对硅钢的铁芯损耗(1.7/50)进行测试。
2 结果与讨论
2.1 Stoney公式的原理及演变
一般认为,涂层的残余应力起源于基体和涂层的热膨胀失配作用,作用原理如图2所示。一般情况下,样品上下同时存在相近厚度的涂层,由于受力平衡因而在宏观上表现为平整的外观。但当样品仅有一侧存在应力涂层时,样品就会发生弯曲,如图3所示。

图2 涂层对取向硅钢应力作用的局部示意图
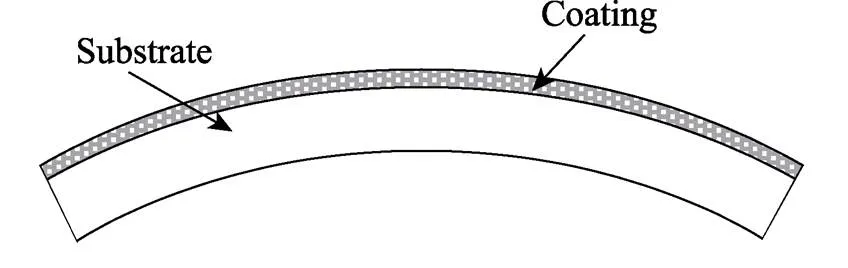
图3 仅有单面涂层情况下取向硅钢的弯曲情况示意图
Stoney[17]于1909年提出了计算薄膜残余应力的公式,见式(1)。该公式利用弯曲形变的曲率半径“”来表征薄膜的残余应力大小,通过基体和薄膜之间力的关系建立等式。考虑到薄膜应力的不均匀性(见图2),实际上Stoney公式计算得到的是应力的平均值。
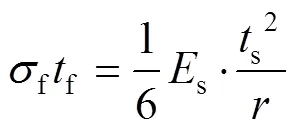
式中:f表示涂层的残余应力,f为涂层厚度,s为基体的弹性模量,s为基板厚度,为基体弯曲的曲率。
Stoney公式自提出以来便得到了广泛应用。目前,有很多关于对Stoney公式在不同应用条件下适用性及修正的讨论[19-20,24-25]:这些公式考虑了包括基体厚度、基体的弯曲程度等在内的因素。其中值得一提的是,关于双轴应力的修正[17]。Stoney公式即式(1)仅仅考虑了单轴应力,然而,实际样品中,计算样品受到的应力均应考虑双轴状态:除样品厚度外的长()和宽()方向。
在基体受到双轴应力的情况下,当基体和薄膜均为各向同性时,涂层对基体产生的张应力与基体应变之间的关系可以表示为:
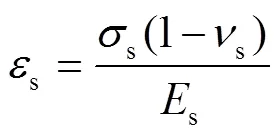
式中:s为基体因涂层受到的应力,s为基体的泊松比,s则表示基体发生的应变。由于薄膜的各向同性,则可认为各方向的张应力值相等,根据式(2),用s/(1-s)代替(1)式中的s,Stoney公式就变为更普遍的形式(3)[18]:
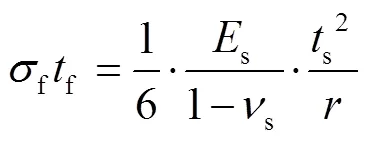
2.2 Stoney公式适用性讨论
Stoney在提出公式时就认为该公式在涂层非常薄的情况下才能够适用[17]。事实上,应用Stoney公式必须满足以下假设[24]:(i)与横向尺寸相比,薄膜和衬底厚度都很小;(ii)薄膜厚度远小于衬底厚度;(iii)基材均匀、各向同性、线性弹性好,薄膜材料各向同性;(iv)衬底边缘附近的边缘效应不重要,所有物理量在与界面平行的位置发生变化时都不变;(v)厚度方向上的所有应力成分在整个材料中消失,且应变和旋转无穷小。因此,若要采用Stoney公式计算涂层的残余应力或基体受到的应力,必须结合取向硅钢及其涂层的实际情况对公式的适用性进行讨论,具体如下所述。
采用扫描电镜分析取向硅钢涂层的典型结构。实际上,取向硅钢的绝缘涂层下方还存在一层硅酸镁底层,因此对涂覆前后样品的状态分别进行分析。图4为取向硅钢为涂覆绝缘涂层前截面的微观状态,可以看到硅酸镁底层的颗粒紧密地附着在基体上,厚度大约为1 μm,平整度较差。图5展示取向硅钢成品绝缘涂层的微观形貌和结构,可以看到绝缘涂层紧密地附着在硅酸镁底层上,二者没有明显的界限,涂层状态均匀致密,涂覆涂层后样品表面变得平整。

图4 硅酸镁底层的截面形貌
根据涂层的结构、成分和特点可知,涂层内部的残余应力是各向同性的。尽管取向硅钢具有锋锐的Goss({110}<001>)织构,存在明显的各向异性,但因晶体结构的高对称性(体心立方α-Fe),晶粒尺寸较大(与单晶类似),因此可认为热膨胀系数不存在各向异性[26-27],故可认为最终作用在硅钢基体上各方向的张应力为各向同性。取向硅钢表面的涂层厚度在1~4 μm左右(参看图1和图5),而钢板的板厚则为0.20~0.30 mm,二者特点满足Stoney公式对于涂层性质和厚度的假设条件(ii)。而关于基体的假设条件中,当被测试样品在状态良好、尺寸恰当的条件下,条件(i)、(iv)和(v)容易得到满足,但是取向硅钢存在明显的各向异性。图6为采用静态拉伸方法获得的(部分)力学性能数据,其中图6a是沿TD方向拉伸的纵向和横向的应力-应变曲线,图6b则为沿RD方向拉伸的纵向和横向的应力-应变曲线,结果显示,横向和纵向的弹性模量和泊松比有明显区别。因此,取向硅钢不满足条件(iii),无法直接使用式(3)来进行计算,需要针对取向硅钢的特点,结合Stoney公式的原理,进行更深入的分析和推导。
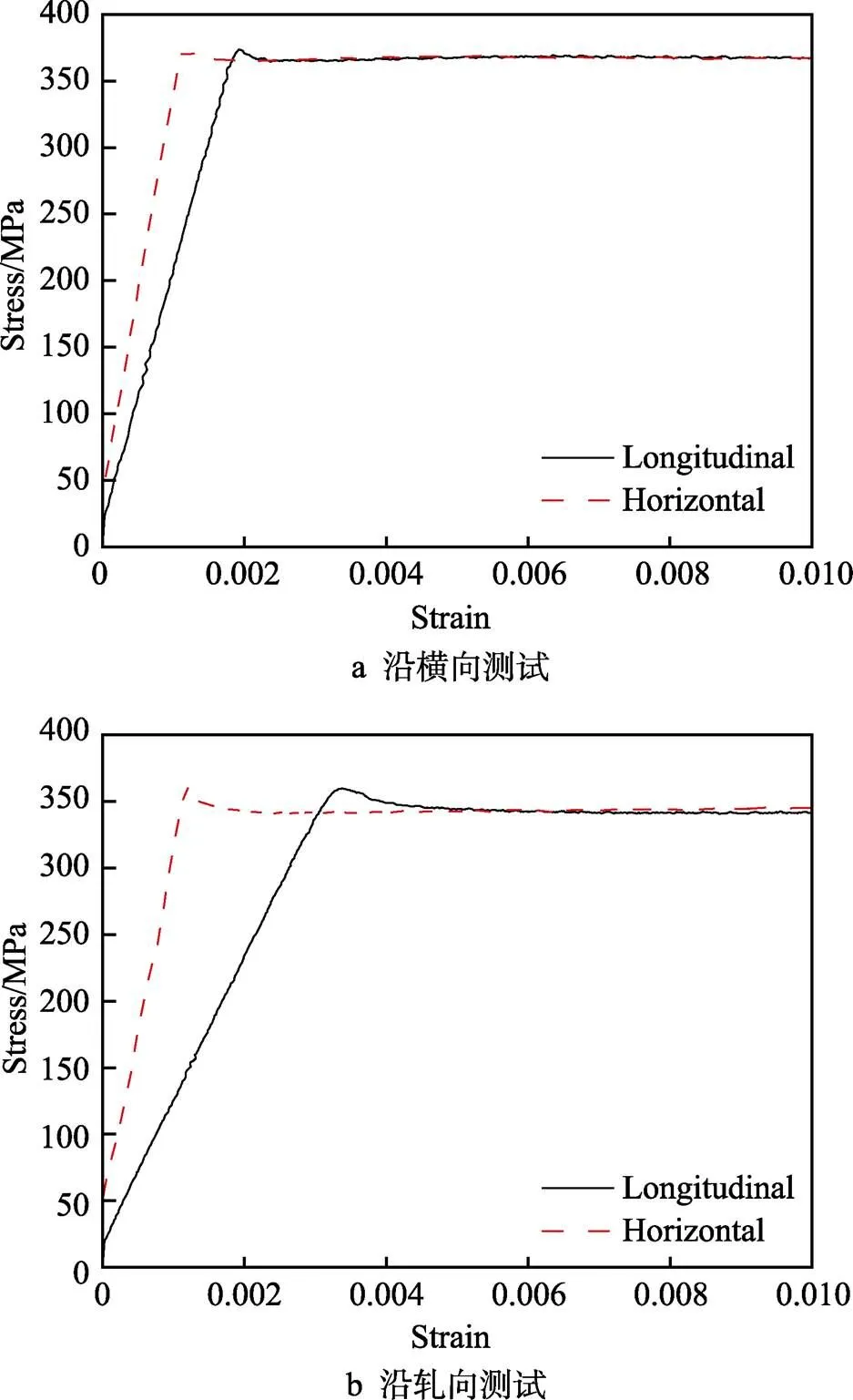
图6 沿两个方向测试的取向硅钢静态拉伸曲线
根据广义的胡克定律,具有弹性正交对称性的各向异性材料各应变分量与应力分量之间的关系如下:
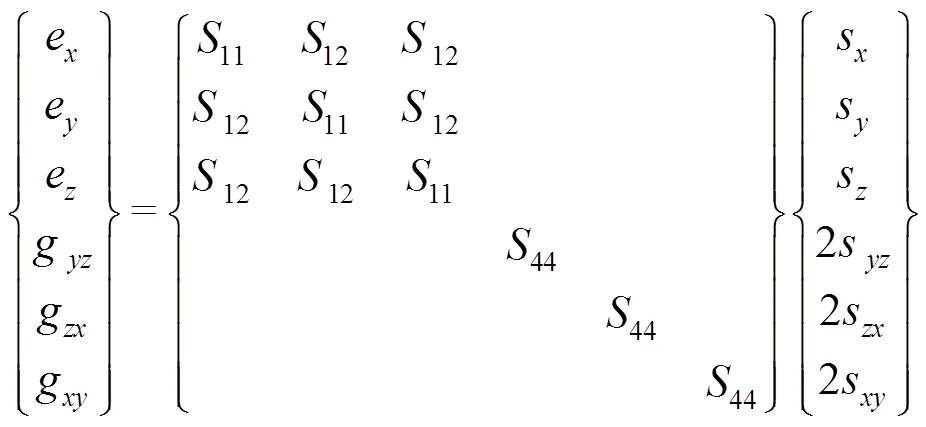
已有学者[28]对Si单晶材料表面薄膜残余应力的计算公式进行推导,公式中采用了材料某些特定方向的S(弹性柔度系数,第一个下标为应变方向,第二个下标为样品受到的应力方向,其他力学性能参数的下标含义相同)来分别表达Si(001)单晶和Si(111)单晶表面膜层的残余应力,公式的表达形式与基体的晶体取向及相应的力学参数密切相关,形式多样且较为复杂。
由于取向硅钢基体所受应力的计算过程中不涉及剪切应力,根据式(4),方向或者方向张应力的计算公式为:

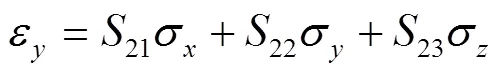
涂层的张应力主要作用在基体的、方向,因此计算过程中可不考虑厚度方向的σ和ε。根据弹性柔顺系数的定义,以方向为例,式(5)可变为式(7)的形式,方向可以类推。其中,基体受到的张应力为各向同性,故σ与σ相等,故式(7)统一表达为s。
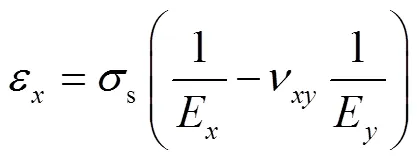
式(7)可做如下理解,方向的应变由两部分组成:仅由方向受到的应力引起的应变与方向的应力导致方向的应变。在式(7)中,ν为方向受力引起的方向发生应变,即沿方向进行拉伸试验所得到的泊松比数据。
根据式(4),正交对称性材料的弹性柔顺系数S=S,结合弹性柔顺系数的定义,可得:
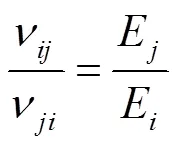
通过测量得到的未涂覆绝缘涂层样品的弹性模量和泊松比数据结果如表1所示。
表1 取向硅钢力学性能数据
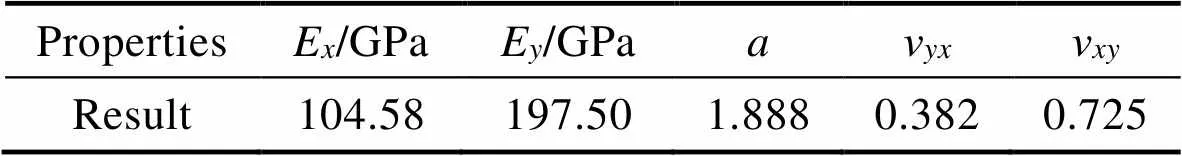
Tab.1 Mechanical properties of grain-oriented silicon steel
在弹性各向同性的材料中,钢铁材料的泊松比一般在0.20~0.30范围内。但因取向硅钢具有各向异性,泊松比数据的“范围”发生了变化,已有许多学者证明[29-31]:各向异性材料的泊松比的限制条件与各向同性材料有很大的不同。LEMPRIERE[32]推导出了具有各向异性的立方晶体材料的泊松比受弹性模量的比例限制,如式(9)所示。

表1中测试的数据符合式(8)和(9)的条件,这说明上述关于力学性能的分析是适用于取向硅钢的。在式(8)中,分别取、为、方向,代入式(7)即可得到基体沿方向或方向受到张应力的计算公式:
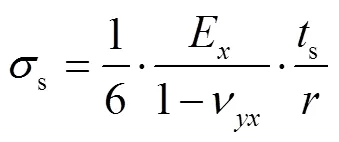
式中:s表示基体受到来自涂层的残余应力,s为基体厚度,E为基体沿方向的弹性模量,则表示基体沿方向弯曲的曲率半径。虽然基体受到的应力为各向同性的,但是由于力学性能的各向异性,沿不同方向得到的曲率值却各不相同。就本文来说,轧向的曲率半径明显小于横向,且更易测量。
本文在Stoney公式和公式(3)的基础上,引入了各向异性材料沿不同位向的力学性能,修正了公式(3),解决了取向硅钢这种各向异性材料受到来自基体的张应力计算的问题。对于大多数材料来说,能够通过静态拉伸试验或其他测量方法获得力学性能数据,测量较为简单,只要将力学性能数据代入式(10)中就能够得到基体的张应力数据。因此,式(10)不仅适用于计算取向硅钢表面膜层的残余应力,还可以用于其他条件类似的材料。当然,使用公式的前提是必须满足Stoney公式的适用条件。
综上,计算取向硅钢绝缘涂层沿某一方向对基体产生的张应力s的计算公式为(10),需要注意的是,本公式考虑的情况是单侧涂层的张应力,当取向硅钢两侧均存在相同的涂层,因力的方向一致,可认为基体所受的应力为双侧应力之和。
2.3 张应力与涂层厚度及铁损之间的关系
张应力可以明显改变取向硅钢的铁损。研究证明[3-5],张应力能够细化磁畴结构,消除匕首畴和90°闭合畴等结构,在一定范围内,对取向硅钢施加张应力将降低铁损,铁损的下降幅度和张应力数值呈线性相关。在实际生产过程中,人们利用涂层对基体产生张应力来实现铁损降低的目的,如硅酸镁底层、TiN类陶瓷涂层、硅溶胶-磷酸盐绝缘涂层等[8-13],涂层种类、涂布方式和涂层涂布量都将对铁损的降低幅度产生影响,因此可以通过改变涂层状态来进一步优化取向硅钢的铁损,这对高磁感取向硅钢来说更重要。
本文计算得到了曲率半径,测试了样品的力学性能,代入式(10)中计算得到样品受到来自绝缘涂层的张应力数据,每组试验样品分别测试了五组数据,具体见表2,可以看到同组样品的张应力计算数据较为稳定,一致性较好。
表2 张应力测试结果
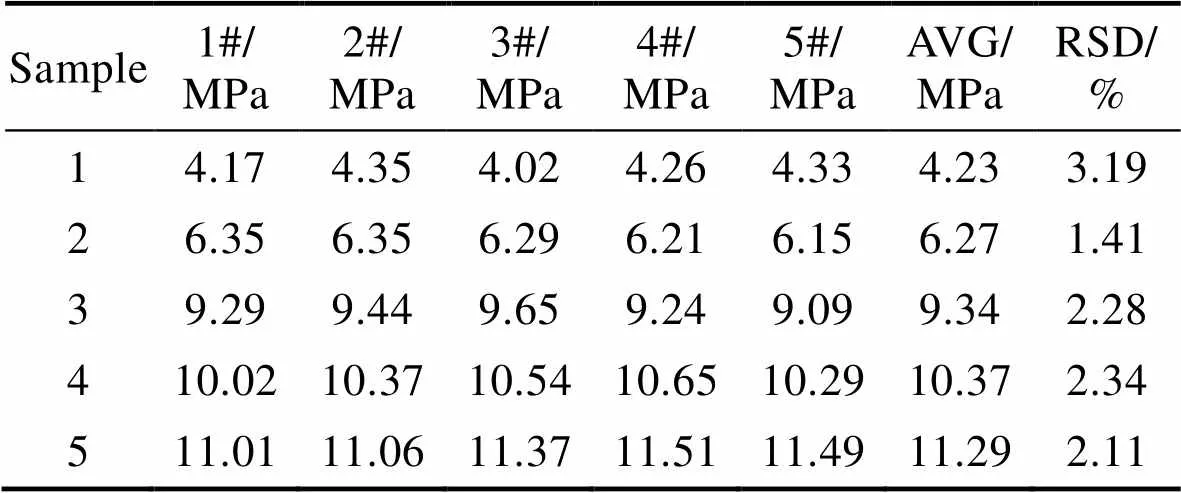
Tab.2 Test result of tensile stress
图7为涂层厚度和基体受到的张应力数据(双面涂层的作用),可知在同样的烧结工艺条件下,随着涂层厚度的增大,基体受到的张应力增加。图8为基体受到来自涂层的张应力对样品铁损的影响,其中,纵坐标的数据为同一样品涂覆应力绝缘涂层后铁损降低的数值。从图8中可以看到,随着张应力的增大,样品的1.7/50的降低幅度越来越大,本文得到的张应力与铁损的数值关系与文献数据[6,8]基本相当。虽然随着张应力的升高铁损不断得到优化,但是对于本文中所采用的涂层类别和涂覆工艺下,绝缘涂层厚度超过1.8 μm时,涂层易于脱落,附着性变差,厚度达到2.0 μm时,附着性极差,已经不满足实际使用需求(随着涂层成分类别的变化,涂层厚度的极限值可能发生变化)。因此,该种类涂层的厚度应控制在合理的范围内,同时满足磁性能、使用性能及生产成本的要求。另外,在实际生产中,应该在满足使用需求的情况下,开发张力更大的涂层,进一步提升产品的磁性能。
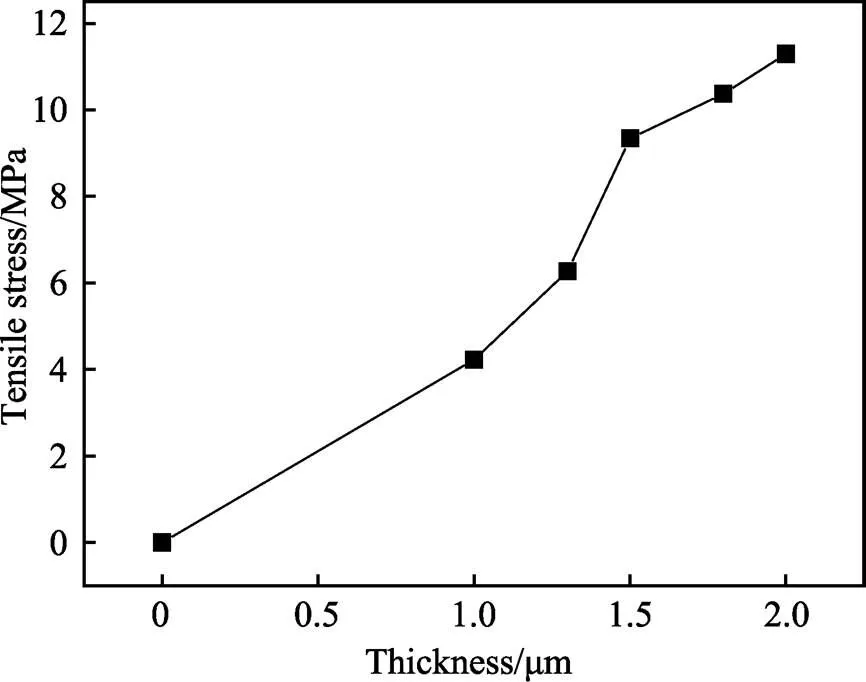
图7 绝缘涂层厚度与张应力的关系

图8 涂层的张应力对铁损的影响
3 结论
1)本文讨论了Stoney公式对取向硅钢的适用性,实际测试了取向硅钢的力学性能,认为取向硅钢符合正交对称各向异性材料的一般规律,在此基础上提出了取向硅钢涂层应力的计算公式,解决了各向异性Stoney公式应用中的问题,此公式还可用于其他满足Stoney公式适用条件且基体为各向异性的情况。
2)本文的绝缘涂层为添加了磷酸盐的胶体二氧化硅涂层,计算了其对取向硅钢产生的张应力,涂层厚度在1~2 μm范围内,双面张应力的计算值为4~11 MPa。
3)随着绝缘涂层厚度的增大,涂层给予基体的张应力增加,而随着张应力的增加,铁损逐渐降低。在满足实际使用需求的前提下,开发大张力的涂层,是优化取向硅钢性能的途径之一。
[1] MATSUO M. Texture control in the production of grain oriented silicon steels[J]. Transactions of the iron & steel institute of Japan, 1989, 29(10): 809-827.
[2] 黎先浩, 孟小涛, 赵鹏飞, 等. 高磁感取向硅钢研发现状与展望[J]. 中国冶金, 2019, 29(1): 1-7. LI X H, MENG X T, ZHAO P F, et al. Present status and future prospect of high permeability grain-oriented silicon steel[J].China metallurgy,2019, 29(1): 1-7.
[3] GNIEWEK J J. Effects of tensile stress on the domain structure in grain-oriented 3.25% silicon steel[J]. Journal of applied physics, 1963, 34(12): 3618-3622.
[4] HOUZE G L. Effect of longitudinal tensile stress on the static and 60 Hz domain structures of grain-oriented siliconsteel[J]. Journal of applied physics, 1969, 40(3): 1090-1091.
[5] PERRYMAN R. Effects of tensile and compressive stress on 3% grain-oriented silicon iron[J]. Journal of physics D: Applied physics, 1975, 8(15): 1901-1909.
[6] OVERSHOTT K J, Foot G. The effect of tensile stress on the power loss of 3% grain-oriented silicon-iron[J]. IEEE transactions on magnetics, 1982, 18(6): 1496-1498.
[7] HEGAB S, Al-Mutawa S. Strain-magnetization properties and domain structures of silicon steel sheets[J]. Electrical engineering in Japan, 2010, 149(2): 10-17.
[8] MOSES A J, Pike E C. Influence of surface coating on transverse magnetostriction in silicon iron[J]. Electrical engineers proceedings of the institution, 1977, 124(6): 583-585.
[9] INOKUT Y. Grain oriented silicon steel sheet with a ceramicfilm characterized by ultra-low iron loss[J]. Vacuum, 1996, 47(6-8): 857-862.
[10] PUZHEVICH R V, KORZUNIN G S, KARENINA L S, et al. Mutual influence of electrical insulating coatings and structural barriers on the level of magnetic losses in anisotropic electrical sheet steel[J]. Physics of metals & metallography, 2009, 108(6): 543-547.
[11] PUZHEVICH R B, DUKHNOV A G, SAMSIKOV E A, et al. Effect of the ground layer on the magnetic properties of highly permeable silicon steel[J]. Metal science & heat treatment, 1986, 28(6): 435-439.
[12] SHIMANAK H, ICHIDA T, KOBAYASHI S, et al. Effect of several stress inducing coatings on magnetostriction property of a high induction 3% silicon steel[J]. IEEE transactions on magnetics, 2003, 15(6): 1595-1597.
[13] SHINGAKI Y, OKABE S. Influence of crystal orientation on magnetic properties in 3% silicon steel with ultra-high tension TiN coating[J]. IEEE transactions on magnetics, 2012, 48(4): 1469-1472.
[14] INOKUTI Y, SUZUKI K. Relation between iron loss and tensile stress induced in silicon steel sheets by TiN, TiCN and TiC coatings[J]. Journal of the vacuum society of Japan, 2009, 46(3): 329-332.
[15] 汪伊丽, 梁天权, 沈晓明, 等. 热障涂层界面应力测试研究进展[J]. 材料导报, 2016, 30(S2): 495-498.WANG Y L, LIANG T Q, SHEN X M, et al. Research progress of interfacial stress measurement in thermal barrier coatings[J]. Materials review, 2016, 30(S2): 495-498.
[16] STONEY G G. The tension of metallic films deposited by electrolysis[J]. Proceedings of the Royal Society of London, 1909, 82(309): 40-43.
[17] JACCODINE R J, SCHLEGEL W A. Measurement of strains at Si-SiO2interface[J]. Journal of applied physics, 1966, 37(6): 2429-2434.
[18] FLINN P A, GARDNER D S, NIX W D. Measurement and interpretation of stress in aluminum-based metallization as a function of thermal history[J]. IEEE transactions on electron devices, 1987, 34(3): 689-699.
[19] CHIU C C. Residual stresses in ceramic coatings as determined from the curvature of a coated strip[J]. Materials science & engineering A, 1992, 150(1): 139-148.
[20] ARDIGO M R, AHMED M, BESNARD A L. Stoney formula: Investigation of curvature measurements by optical profilometer[J]. Advanced materials research, 2014, 996(8): 361-366.
[21] SHIRI S, ASHTIJOO P, ODESHI A, et al. Evaluation of Stoney equation for determining the internal stress of DLC thin films using an optical profiler[J]. Surface & coatings technology, 2016, 308(11): 98-100.
[22] WEN J, WEI Y, CHENG Y T. Examining the validity of Stoney-equation for, in-situ, stress measurements in thin film electrodes using a large-deformation finite-element procedure[J]. Journal of power sources, 2018, 387(5): 126-134..
[23] KIM J S, PAIK K W, Oh S H. The multilayer-modified Stoney′s formula for laminated polymer composites on a silicon substrate[J]. Journal of applied physics, 1999, 86(10): 5474-5479.
[24] FREUND L B, FLORO J A, CHASON E. Extensions of the Stoney formula for substrate curvature to configurations with thin substrates or large deformations[J]. Applied physics letters, 1999, 74(14): 1987-1989.
[25] KLEIN C A. How accurate are Stoney′s equation and recent modifications[J]. Journal of applied physics, 2000, 88(9): 5487-5489.
[26] SIROTIN Y I, SHASKOL'SKAYA M P. Fundamentals of crystal physics[M]. Moscow: Science, 1979.
[27] ZAMKOVSKAYA A, MAKSIMOVA E. Anisotropic thermal expansion in crystals of different categories[j]. Journal of physics conference series, 2015, 58: 661.
[28] JANSSEN G C A M, ABDALLA M M, KEULEN F V, et al. Celebrating the 100th anniversary of the Stoney equation for film stress: Developments from polycrystalline steel strips to single crystal silicon wafers[J]. Thin solid films, 2009, 517(6): 1858-1867.
[29] HAYES M, SHUVALOV A. On the extreme values of Young′s Modulus, the Shear Modulus, and Poisson′s ratio for cubic materials[J]. Journal of applied mechanics, 1998, 65(3): 786-787.
[30] TING T C T, CHEN T Y. Poisson′s ratio for anisotropic elastic materials can have no bounds[J]. Quarterly journal of mechanics & applied mathematics, 2005, 58(1): 73-82.
[31] WALTON R I, SMITH C W, LETHBRIDGE Z A D, et al. Elastic anisotropy and extreme Poisson′s ratios in single crystals[J]. Acta materialia, 2010, 58(19): 6444-6451.
[32] LEMPRIERE B M. Poisson′s ratio in orthotropic materials[J]. AIAA journal, 1968, 6(11): 2226-2277.
Based on Applicability Analysis of Stoney Equation: Calculation of Tensile Stress Induced in Grain-oriented Silicon Steel by Insulation Coating
1,2,2,3,2,1,2,2
(1.School of Materials Science and Engineering, University of Science and Technology Beijing, Beijing 100083, China; 2.Shougang Zhixin Qian'an Electromagnetic Material Co. Ltd, Qian'an 064404, China; 3.Beijing Shougang Co., Ltd, Qian'an 064404, China)
The work aims to optimize the tensile stress of the coating, so as to improve the magnetic properties of grain-oriented silicon steel. The thickness and microstructure of colloidal silica insulation coating with phosphate were analyzed by SEM and GDS and the mechanical properties of substrate along different direction were acquired by tensile test. Based on the anisotropy of grain-oriented silicon steel and the real state of coating, the applicability of Stoney equation to the grain-oriented silicon steel coating was discussed. The anisotropy of grain-oriented silicon steel did not meet the applicable conditions of Stoney equation and the mechanical properties of grain-oriented silicon steel tested in practice showed that the grain-oriented silicon steel conformed to the general law of orthotropic material. Based on that, the equation was given to calculate the tensile stress induced in the substrate of oriented silicon steel by the colloidal silica insulation coating under different technology parameters. The tensile stress was 4~11 MPa when the coating thickness was within 1~2 microns. The equation for calculating the tensile stress is not only applicable to grain-oriented silicon steel, but also applicable to similar cases where other substrates are anisotropic. Through calculation of tensile stress, the stress and thickness of the insulation coating have a positive correlation and the iron loss reduce with increasing of the stress induced in substrate by the coating. Therefore, the research and development of insulation coating with higher tensile stress is the effective method to improve the magnetic properties of grain-oriented silicon steel.
grain-oriented silicon steel; insulation coating; tensile stress; Stoney equation; anisotropy
2019-08-10;
2019-11-03
LIU Zhao-yue (1987—), Female, Doctoral candidate, Research focus: research and development of electrical steel.
杨平(1959—),男,博士,教授,博士研究生导师,主要研究方向为晶体材料的形变、再结晶、相变及织构。邮箱:yangp@mater.ustb.edu.cn
Corresponding author:YANG Ping (1959—), Male, Doctor, Professor, Doctoral supervisors, Research focus: deformation, recrystallization, phase transition and texture of crystalline materials. e-mail: yangp@mater.ustb.edu.cn
刘兆月, 司良英, 马家骥, 等. 基于Stoney公式适用性分析——取向硅钢绝缘涂层张应力的计算[J]. 表面技术, 2020, 49(6): 146-151.
TG174.4;TB34
A
1001-3660(2020)06-0146-06
10.16490/j.cnki.issn.1001-3660.2020.06.017
2019-08-10;
2019-11-03
刘兆月(1987—),女,博士研究生,主要研究方向为电工钢材料的研发。
LIU Zhao-yue, SI Liang-ying, MA Jia-ji, et al. Based on applicability analysis of stoney equation: calculation of tensile stress induced in grain-oriented silicon steel by insulation coating[J]. Surface technology, 2020, 49(6): 146-151.
