采用神经网络和遗传算法优化磁粒研磨TC4弯管工艺参数
2020-06-30李文龙陈燕赵杨吕旖旎
李文龙,陈燕,赵杨,吕旖旎
采用神经网络和遗传算法优化磁粒研磨TC4弯管工艺参数
李文龙,陈燕,赵杨,吕旖旎
(辽宁科技大学 机械工程与自动化学院,辽宁 鞍山 114051)
提高研磨TC4弯管内表面质量及加工效率,对磁粒研磨加工工艺参数进行优化。首先设定最优表面质量为优化的目标,然后将影响磁粒研磨TC4弯管内表面质量的四个主要工艺参数作为优化对象,对所要建立的神经网络隐含层节点数的个数进行试验,并选择最优值,之后建立反映TC4弯管内表面粗糙度和主要工艺参数的非线性映射模型,最终使用遗传算法得到TC4弯管内表面粗糙度最优值和磁粒研磨加工TC4弯管内表面的最优工艺参数组合,并且通过试验验证其预测结果的精确性。通过建立结构为4-5-1的BP神经网络,并利用遗传算法的预测,得到了磁粒研磨加工TC4弯管最优工艺参数配置组合:磁极转速为570 r/min,加工间隙为2.0 mm,磨料粒径为178 μm(80目),进给速度为80 mm/min。使用BP神经网络创建的反映TC4弯管内表面粗糙度与加工TC4弯管内表面工艺参数之间的映射模型具有较好的精度,同时应用遗传算法全局寻优得到了最佳的工艺参数,是一种准确度较高的优化磁粒研磨TC4弯管内表面加工工艺参数的新方法。
磁粒研磨;弯管;内表面;表面粗糙度;BP神经网络;遗传算法;TC4钛合金
TC4钛合金因其具有耐高温、密度小以及比强度较高等优点,被广泛应用于航空航天和其他机械领 域[1],用于制造一些精密仪器中的弯管或异型管等管路。弯管在加工过程中,外侧因受到拉应力的作用,会产生不可避免的弯裂,严重影响管件的使用寿命;内侧因受到压应力的作用,会产生褶皱,并且产生微裂纹。微裂纹的存在会引发应力集中的问题,严重时会产生疲劳断裂,使管件工作时的可靠性大大降低[2-7]。褶皱和粗糙严重影响了液体或气体在管件内的均匀流动,易产生喘振等影响工作性能的不利因素[8-11]。因此,降低管件内表面的表面粗糙度变得尤为重要。
相比其他特种加工工艺,磁粒研磨在加工弯管内表面时,具有自适应性、自锐性、升温小、无刀补等优点[12]。肖作义[13]提出了影响磁粒研磨的主要参数,分析了不同工艺参数对研磨之后表面质量的影响。肖阳等[14]对磁力研磨钛合金进行了研究,并对其加工工艺参数进行了分析,得到了较好的表面粗糙度值,但在选择最优工艺参数时,采用的是单因素实验方法,没有考虑在降低工件表面粗糙度的过程中,各工艺参数之间存在着相互影响的作用。
基于磁粒研磨加工的特点以及表面粗糙度与工艺参数之间存在非线性的特征,采用BP神经网络与遗传算法,可预测最佳的工艺参数。与传统的优化方法相比,神经网络具有高的预测精度、较强的自学习能力和非线性映射能力。因此,本文在研磨试验数据的基础上,构建能够表达TC4弯管内表面的表面粗糙度与加工工艺参数之间关系的BP神经网络,并采用遗传算法预测最佳的工艺参数。
1 试验
1.1 原理
磁粒研磨加工弯管内表面原理如图1所示。在TC4弯管外部配置永磁极,利用磁力线能穿透非导磁材料的特性,在所要加工的弯管内部形成磁场[15]。磁性磨料从管的端部放入管中,放置在管内的磁性磨料在外部磁场的作用下,沿着磁力线排布,磁性磨料仿形贴附于工件内表面形成磁粒刷[16]。外部磁极在皮带的带动下做旋转运动,利用磁场力带动弯管内部的磁性磨料与所要加工的管件发生相对运动。磁性磨料形成的磁粒刷在磁场力的作用下压在工件内壁,管件内部的磁性磨料上切削刃的硬度远大于所加工的工件的硬度。在磁性磨料随外部磁极转动的过程中,磨料上的切削刃会切入所加工的工件,从而起到对内表面抛光的作用。

图1 磁粒研磨加工弯管内表面原理
1.2 装置及条件
试验使用的磁粒研磨加工TC4弯管内表面的装置结构如图2所示,主体由多自由度机械臂和磁粒研磨装置构成。在对弯管进行加工时,将弯管固定于工作台上,将磁性磨料和适量的油性研磨液放入管件内部,试验所使用的磁性磨料尺寸为150(100目)、178(80目)、250 μm(60目),加工时间为30 min。研磨装置在机械臂带动下,沿着管件轴线方向往复运动,机械臂往复运动速度的调整精度为10 mm/min。研磨装置通过皮带与伺服电机配合,在伺服电机的驱动下,带动研磨装置使磁极旋转,伺服电机的调整精度为10 r/min。本实验选用的管件为TC4弯管,管件尺寸为20 mm×18 mm(外径×内径),试验时加工长度为80 mm。使用NdFeB(N35)永磁体,永磁体尺寸为15 mm×15 mm×10 mm。聚磁装置采用尺寸为15 mm×15 mm×10 mm的碳素钢,其锥度为25°。在弯管的内部放置8 mm球形磁极作为辅助磁极。使用劳力恩SR-991珩磨油(油性)作为研磨液。将试验所使用的TC4管件沿轴向抛开,利用JB-8E表面粗糙度测量仪对试验前、后的管件内表面进行记录。采用VHX-500F超景深显微镜对其表面微观形貌进行观察。
1.3 试验设计
选择磁极转速、加工间隙、磨料粒径、进给速度等4种工艺参数进行研究。根据各工艺参数的经验值,选择各个因素的取值范围,试验方案见表1。利用线切割,将试验所使用的管件沿轴向剖开,利用粗糙度仪对工件原始表面多个部位进行测量。由于工件内圆周面表面粗糙度无较大差异,故采用多点测量取平均值的方法,确定最终的表面粗糙度值,其平均表面粗糙度值为1.34 μm。将剖开的工件复合固定,对管件内表面进行磁粒研磨加工,之后将固定的管件拆开,利用粗糙度仪重新测量,采用多点测量取平均值的方法确定加工后的表面粗糙度。通过加工前、后的表面粗糙度差值,可以直观地反映磁粒研磨对管件加工的效果。
表1 试验方案
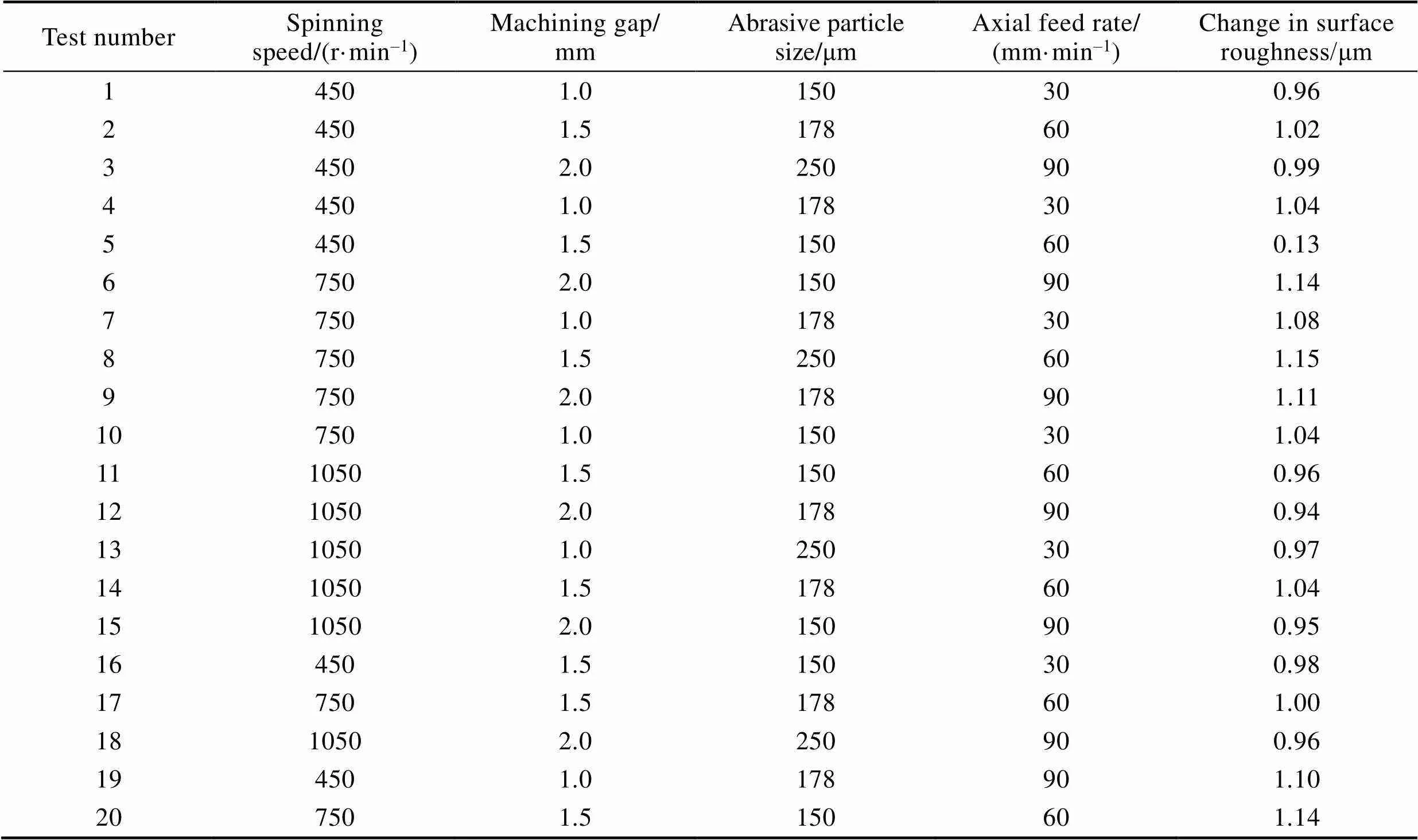
Tab.1 Experimental program
2 神经网络的建立与测试
2.1 算法流程
由于磁极转速、磨料粒径、加工间隙、进给速度这些加工参数,在降低工件表面粗糙度的过程中存 在着相互作用。因此,选择一种具有良好容错性的数学方法,建立用于反映表面粗糙度与加工参数之间关系的数学模型就变得尤为重要。算法的流程如图3 所示。
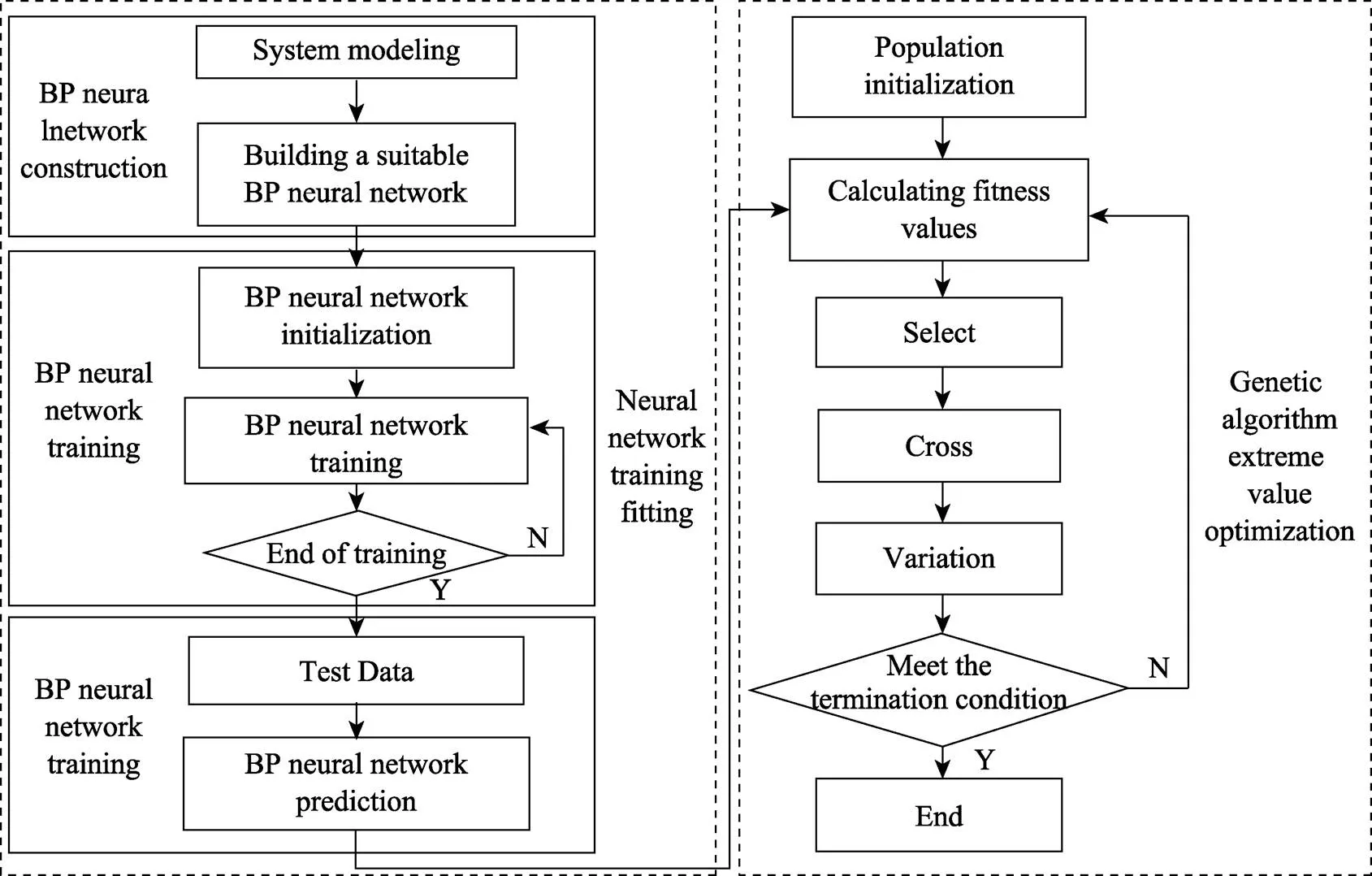
图3 算法流程
2.2 BP神经网络模型的建立
BP(back propagation)神经网络不仅有很强的容错性,还拥有不凡的非线性映射能力[17]。与传统的数学模型相比,BP神经网络具有自我学习的能力,通过对实验数据的学习,从而建立可靠的数学模型,并且可以对发展的趋势进行预测。采用BP神经网络进行建模时,不可避免地存在一些不足,其隐含层的个数一般根据经验计算[18],而隐含层神经元的数量不同,往往会使网络预测的精确性产生较大的偏差。当隐含层神经元不足时,网络无法进行充分的学习,不能保证训练后的准确性;当隐含层神经元过多时,网络易产生过度拟合的情况[19]。在对加工工艺参数和表面粗糙度的建模过程中,还需要对隐含层的个数进行讨论。
本模型为三层网络结构,如图4所示。使用磁极转速、加工间隙、磨粒粒径和进给速度作为网络的输入,将研磨前、后的表面粗糙度的差值Δ作为输出。输入层中的节点数=4,输出层中的节点数=1。
由于每个工艺参数的数值在数量级上有所不同,故需要归一化处理各个参数[20]。将数据归一化后输入网络,并且训练。输入层与隐含层间使用‘tansing’函数进行传递,隐含层与输出层间使用‘purelin’函数进行传递。将Levenberg-Marquardt算法作为神经网络的训练法。网络的迭代次数设置为200代,学习速率拟定为0.2,训练误差设定为0.0001。目前,隐含层节点数多采用经验公式(1)来确定[21]。
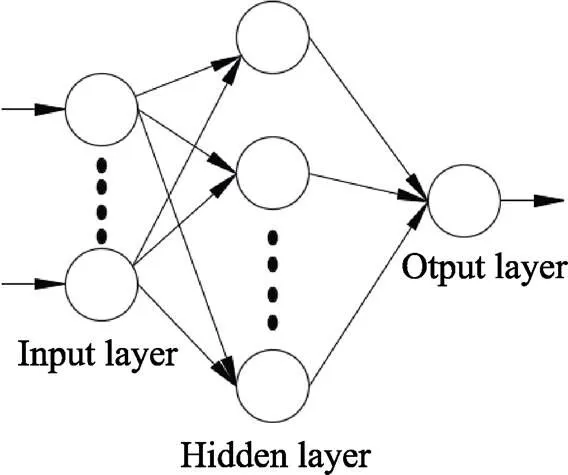
图4 BP神经网络结构
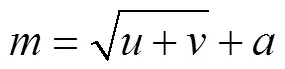
式中:表示隐含层中的神经元节点的数量,如果存在小数,则它需要向上进一位;一般选取1~10的常数,因此隐含层的节点数范围为3~13。在获得的隐含层节点数中,选取使网络预测效果最佳的节 点数。
适当的隐含层节点数可以提高神经网络的预测精度。当选择不同数量的隐含层节点时,预测的值将会存在不同程度的偏差。因此,将预测值与真实值之间的误差百分比平均值作为判断隐含层节点数是否合理的依据,见式(2)。
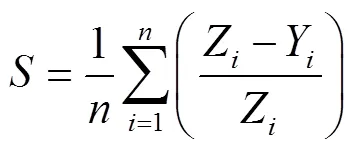
从图5中可以得出,当隐含层节神经元的数量为5,的值最接近0,神经网络的预测误差最小。可以推断出,当隐含层节点的数量是5时,预测精度最好。隐含层神经元节点数量为5的网络结构如图6所示。
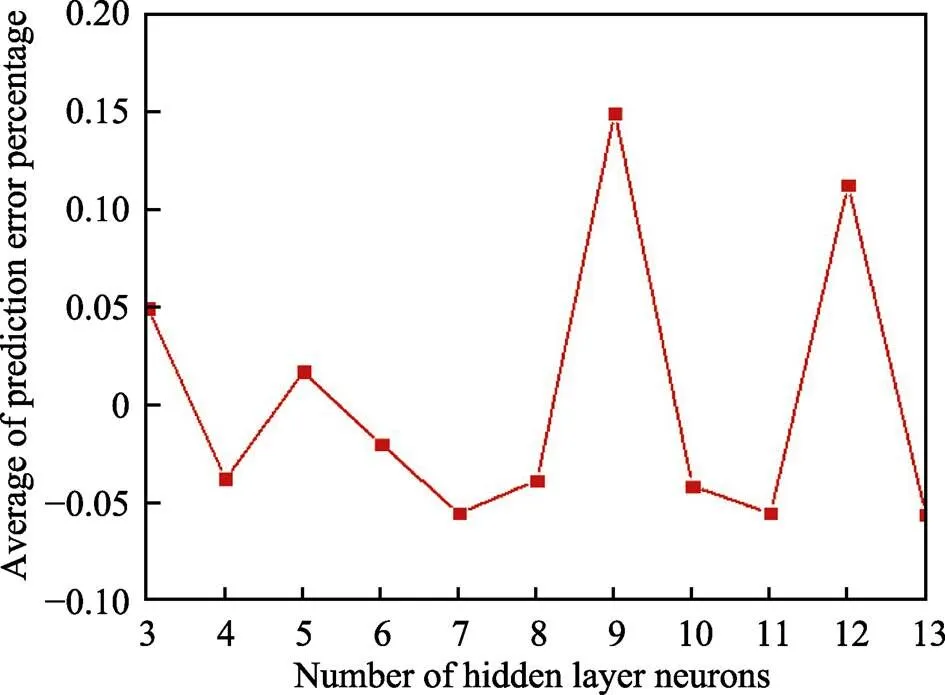
图5 不同隐含层节点数的误差百分比平均数
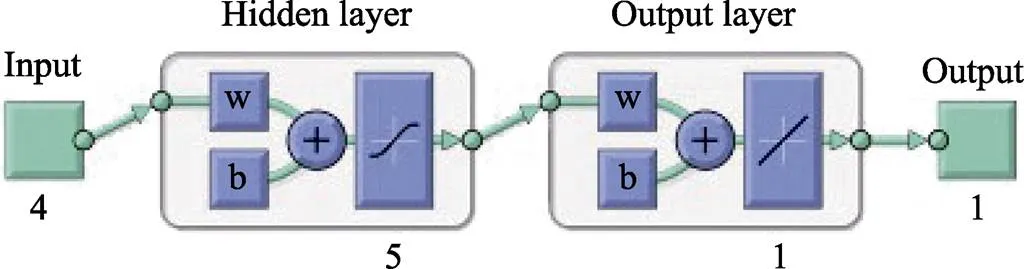
图6 网络结构
2.3 BP神经网络模型的测试
随机选择15组数据用来训练BP神经网络,在经过训练后,可以用于表达非线性函数输出[22]。其余5组数据作为神经网络拟合性能的测试,拟合结果如图7所示。可以看出,除了第4组数据的误差较大(9%)外,其余组的预测数值都和实际值相差不大。预测效果相对理想,反映了训练之后的神经网络具备一定的精确性和较好的预测性。
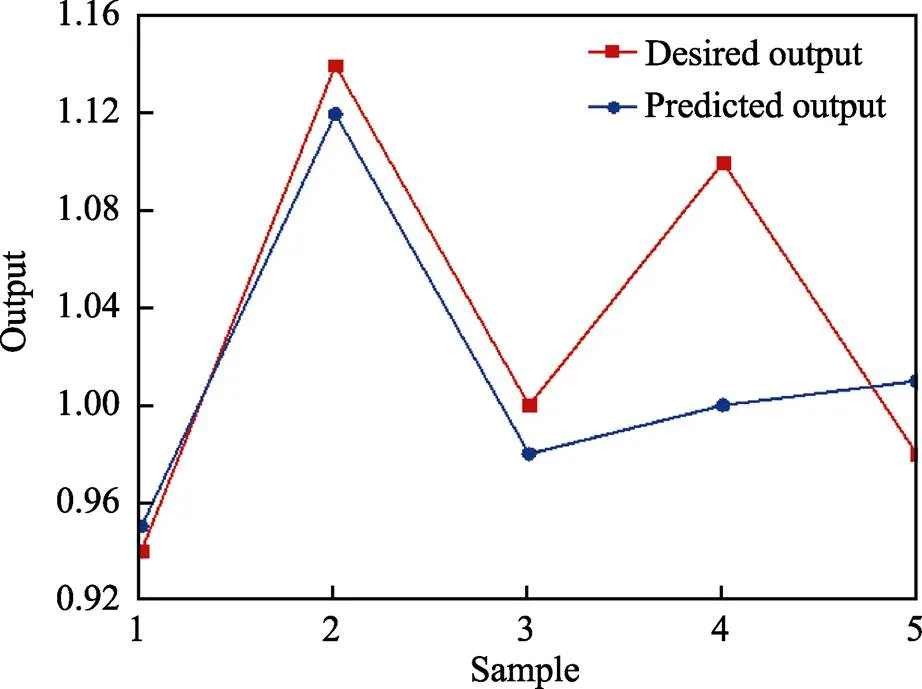
图7 随机抽取样本值与预测值结果对比
3 遗传算法设计及验证
3.1 遗传算法设计
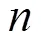
在初始种群的选择上,追求最佳效果。如果初始种群数量过于庞大,则会降低运行速度,影响效率;如果初始种群太少,则有可能将最优解忽略[25]。工艺参数范围见表2,随机生成200个个体,数值来自工艺参数的取值范围,将它们作为初始种群。
表2 工艺参数取值范围
Tab.2 Process parameter value range
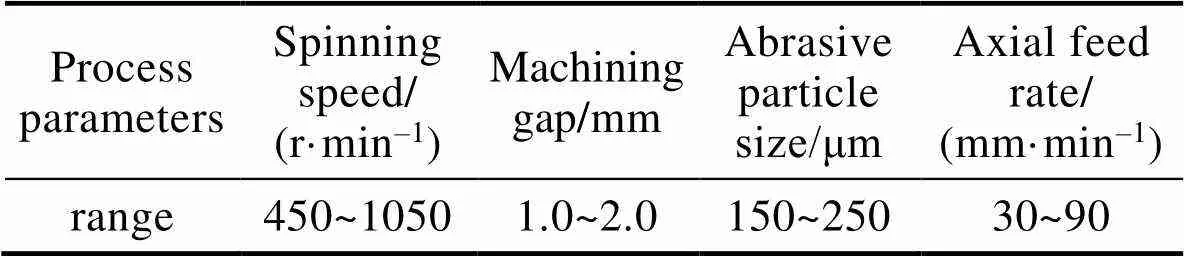
将生成的个体传入已创建完成的BP网络模型,最后神经网络得到的就是目标函数值:
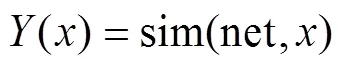
式中:net为已经构建好的BP神经网络模型;为目标函数值;sim为仿真函数;为网络的输入。
选择操作是把适应度看作判断的标准。个体的适应度越高,则它排的位置越靠前,被选择的可能性越大;相反,个体的适应度越低,则排的位置越靠后,被选择的可能性越低。经过不停地选择,从而不断接近最优解。交叉操作是随机选定的个体重组和创造新个体。采用变异的操作随机地将某个个体中的某一基因进行变化,通过这种方式得到不同“子”个体。使用随机遍历抽样法作为选择算子,变异概率m= 0.05,交叉概率c=0.7,遗传算法以迭代次数200次时终止。
利用遗传算法具有全局寻优的功能,在经历200次迭代遗传与进化,最终获得了最佳的工艺参数。max=1.2147,即最优的表面粗糙度为0.1253 μm。获得磁粒研磨TC4弯管的最优参数组合为:=[576.798, 1.7718, 172.9354, 77.364]。将网络得到的预测数据进行圆整,因磁极转速过高时,磁性磨粒在管件内部 相对外部旋转磁极会发生滞后现象,从而对研磨效果产生影响,故磁极转速的圆整采用向下圆整的方法。磨料粒径尺寸有国家标准,与网络预测得到的粒径 值相近的国家标准为178 μm(80目)。最终得到的最优工艺参数:磁极转速为570 r/min,加工间隙为2.0 mm,磨料粒径为178 μm(80目),进给速度为80 mm/min。
3.2 试验检验
利用获得的研磨加工工艺参数对TC4弯管内表面进行研磨,从而对BP神经网络遗传算法的准确性进行验证。利用JB-8E触针式粗糙度测量仪对加工之后的TC4弯管内表面进行测量,并使用超景深显微镜对其表面微观形貌进行观察。在制造管件的过程中,由于加工手段的原因,会产生一些凹坑或凸起。从图8a中可以看出,原始表面粗糙不平,并且具有较深的沟壑,其表面粗糙度为1.341 μm,如图8b所示。利用获得的最优工艺参数进行研磨,如图8c所示。研磨之后其表面十分平整,其原始沟壑得到去除,并且呈现出致密均匀的状态。经测量,其表面粗糙度为0.113 μm,如图8d所示。与预测值相接近,说明BP神经网络遗传算法能够较好地对实验数据进行预测并得到最优值。
图8 工件微观形貌与粗糙度
4 结论
1)建立了磁粒研磨TC4弯管工艺参数与表面粗糙度的BP神经网络映射模型,研究了不同隐含层神经元数量对网络误差造成的不同影响。最后确定隐含层节点数为5时,本网络的精度误差最小。
2)利用试验数据,建立了BP神经网络模型,其网络结构为4-5-1,并且通过预测得到了最优的工艺参数和表面粗糙度。经过实际验证发现,预测的最优值与加工之后的测量值相差甚微。证实了创建的神经网络模型一方面具备较强的预测能力,另一方面还拥有较好的准确性。
3)通过已经建立的BP神经网络模型并进行遗传算法全局寻优,得到了磁粒研磨TC4弯管内表面加工工艺参数的最优配置组合,并且通过试验得到了较高的表面质量。
[1] 刘咏, 王海兵, 黄伯云, 等. 机械合金化方法制备细晶钛合金[J]. 中南工业大学学报(自然科学版), 2002, 33(3): 258-260. LIU Yong, WANG Hai-bing, HUANG Bo-yun, et al. Preparation of fine-grained titanium alloy by mechanical alloying method[J]. Journal of Central South University ofTechnology(natural science edition), 2002, 33(3): 258-260.
[2] 杜宇, 郭荻子, 刘伟, 等. CT20钛合金薄壁管材数控冷弯成形行为研究[J]. 钛工业进展, 2014, 31(5): 10-13. DU Yu, GUO Di-zi, LIU Wei, et al. Research on deformation behaviors of CT20 titanium alloy thin-walled tubesduring numerically controlled bending[J]. Titanium industry progress, 2014, 31(5): 10-13.
[3] 张敬文, 鄂大辛, 李延民, 等. 弯模间隙对5A06管弯曲横截面畸变及壁厚变化的影响[J]. 精密成形工程, 2012, 4(2): 19-22. ZHANG Jing-wen, E Da-xin, LI Yan-min, et al. Effects of clearance on cross sectional distortion and wall thickness variation of 5A06 tube[J]. Journal of netshape forming engineering, 2012, 4(2): 19-22.
[4] SHLYANNIKOV V N, TUMANOV A V, BOYCHENKO N V, et al. Loading history effect on creep-fatigue crack growth in pipe bend[J]. International journal of pressure vessels and piping, 2016, 139-140: 86-95.
[5] AMR A O, MOHAMED M M, HANY F A. Effect of local wall thinning on shakedown regimes of pressurized elbows subjected to cyclic in-plane and out-of-plane bending[J]. International journal of pressure vessels and piping, 2015, 134: 11-24.
[6] YANG H, LI H, ZHAN M. Friction role in bending behaviors of thin-walled tube in rotary-draw-bending under small bending radi[J]. Journal of materials processing tech, 2010, 210(15): 2273-2284.
[7] LU Shi-qiang, FANG Jun, WANG Ke-lu. Plastic deformation analysis and forming quality prediction of tube NC bending[J]. Chinese journal of aeronautics, 2016, 29(5): 1436-1444.
[8] 李彦江, 张立圣, 刘永寿, 等. 飞机燃油管路压力脉动分析[J]. 飞机设计, 2009, 29(5): 37-42. LI Yan-jiang, ZHANG Li-sheng, LIU Yong-shou, et al. Analasis of pressure surge in aircraft fuel pipelines[J]. Aircraft design, 2009, 29(5): 37-42.
[9] PISARENCO M, LINDEN B V D, TIJSSELING A, et al. Friction factor estimation for turbulent flows in corrugated pipes with rough walls[J]. Journal of offshore mechanics and arctic engineering, 2009, 133(1):011101-011109.
[10] 张昕, 纪昌知, 姜敏, 等. 相对粗糙度和雷诺数对90°弯管局部阻力系数的影响[J]. 水力发电学报, 2013, 32(4): 88-93. ZHANG Xin, JI Chang-zhi, JIANG Min, et al. Influence of relative roughness and Reynolds number on local resistance coefficient of 90°-bend pipeline[J]. Journal of hydroelectric engineering, 2013, 32(4): 88-93.
[11] GORJI S, SEDDIGHI M, ARIYARATNE C, et al. A comparative study of turbulence models in a transient channel flow[J]. Computers and fluids, 2014, 89: 111-123.
[12] 严正伟, 陈燕, 宋宗朋. 添加柱形辅助磁极研磨弯管内表面的试验研究[J]. 组合机床与自动化加工技术, 2017(10): 141-145. YAN Zheng-wei, CHEN Yan, SONG Zong-peng. Study on the polishing of inner surface of bending pipe with the cylindrical auxiliary magnetic pole[J]. Modular machine tool & automatic manufacturing technique, 2017(10): 141- 145.
[13] 肖作义. 磁粒研磨加工机理的研究[J]. 机械制造, 2004, 42(12): 39-41. XIAO Zuo-yi. Study on the mechanism of magnetic particle grinding[J]. Machinery, 2004, 42(12): 39-41.
[14] 肖阳, 孙友松, 陈光忠. 永磁场磁力研磨TC11钛合金的实验研究[J]. 表面技术, 2017, 46(2): 229-234. XIAO Yang, SUN You-song, CHEN Guang-zhong. Experimental study of magnetic abrasive finishing of TC11 titanium alloy in permanent magnetic field[J]. Surface technology, 2017, 46(2): 229-234.
[15] 韩冰, 刘立鑫, 陈燕. 磁力研磨法加工弯管内表面的工艺参数优化[J]. 中国机械工程, 2015, 26(6): 814-817. HAN Bing, LIU Li-xin, CHEN Yan. Optimization of process parameters on magnetic abrasive finishing to inner surface of bending pipe[J]. China mechanical engineering, 2015, 26(6): 814-817.
[16] 陈燕, 李龙邦, 曾加恒, 等. 航空发动机钛合金导管内表面精密研磨试验研究[J]. 航空制造技术, 2018, 61(9): 40-46. CHEN Yan, LI Long-bang, ZENG Jia-heng, et al. Study on precision grinding of inner surface of titanium alloy pipe of aeroengine[J]. Aeronautical manufacturing technology, 2018, 61(9): 40-46.
[17] 颜七笙, 游泳, 杨志辉. BP网络结构设计与算法探讨[J]. 科技广场, 2005(3): 36-38. YAN Qi-sheng, YOU Yong, YANG Zhi-hui. Discuss on algorithm and design of BP neural network[J]. Science mosaic, 2005(3): 36-38.
[18] 沈花玉, 王兆霞, 高成耀, 等. BP神经网络隐含层单元数的确定[J]. 天津理工大学学报, 2008, 24(5): 13-15. SHEN Hua-yu, WANG Zhao-xia, GAO Cheng-yao, et al. Determining the number of BP neural network hidden layer units[J]. Journal of Tianjin University of Technology, 2008, 24(5): 13-15.
[19] 朱旭东. BP网络样本数据预处理技术研究[D]. 长沙: 国防科学技术大学, 2015. ZHU Xu-dong. Research on BP network sample data preprocessing technology[D]. Changsha: National University of Defense Technology, 2015.
[20] 柳小桐. BP神经网络输入层数据归一化研究[J]. 机械工程与自动化, 2010(3): 122-123. LIU Xiao-tong. Study on Normalization of input layer data of BP neural network[J]. Mechanical engineering & automation, 2010(3): 122-123.
[21] 王嵘冰, 徐红艳, 李波, 等. BP神经网络隐含层节点数确定方法研究[J]. 计算机技术与发展, 2018, 28(4): 31-35.WANG Rong-bing, XU Hong-yan, LI Bo, et al. Research on method of determining hidden layer nodes in BP neural network[J]. Computer technology and development, 2018, 28(4): 31-35.
[22] 徐新爱, 谢闰根. 基于神经网络遗传算法求非线性系统的最优解[J]. 江西教育学院学报, 2013, 34(3): 20-23. XU Xin-ai, XIE Run-gen. Optimal solution to nonlinear system based on the neural network genetic algorithm[J]. Journal of Jiangxi Institute of Education, 2013, 34(3): 20-23.
[23] 张敏辉, 赖麟, 孙连海. 基于遗传算法的研究与Matlab代码的实现[J]. 四川教育学院学报, 2012, 28(1): 115-117. ZHANG Min-hui, LAI Lin, SUN Lian-hai. Research basedon genetic algorithm and implementation of matlab code[J]. Journal of Sichuan College of Education, 2012, 28(1): 115-117.
[24] 陈国龙, 蔡金锭. 遗传算法在求解全局优化问题中的应用[J]. 福州大学学报(自然科学版), 1999, 27(5): 14-18. CHEN Guo-long, CAI Jin-ding. Application of genetic algorithm in solving global optimization problems[J]. Journal of Fuzhou University (natural science edition), 1999, 27(5): 14-18.
[25] 唐世浩, 朱启疆. 遗传算法中初始种群与交叉、变异率对解的影响及其解决方案[J]. 科技通报, 2001, 17(3): 1-7. TANG Shi-hao, ZHU Qi-jiang. The influence of initial population and crossover and mutation rate on solution in genetic algorithm and its solution[J]. Bulletin of science and technology, 2001, 17(3): 1-7.
Optimizing Technological Parameters of Magnetite Grinding TC4 Elbow by Neural Network and Genetic Algorithms
,,,
(School of Mechanical Engineering and Automation, University of Science and Technology Liaoning, Anshan 114051, China)
The work aims to optimize the process parameters of magnetic abrasive finishing to improve the magnetic abrasive finishing quality and processing efficiency of the inner surface of the TC4 elbow. Firstly, the optimum surface quality was set as an optimization target. Secondly, the four main process parameters affecting the inner surface quality of the magnetic abrasive finishing were taken as an optimization object, the number of nodes in the hidden layers of the neural network to be set up was tested to select optimal value. Thirdly, a nonlinear mapping model that reflects the internal surface roughness and main process parameters of the TC4 elbow was establish. Finally, by using genetic algorithm, the optimal surface roughness of TC4 elbow and the optimal technological parameter combination of magnetic abrasive finishing for TC4 elbow was obtained, and the accuracy of the prediction results was verified by experiments. By establishing a BP neural network with a structure of 4-5-1 and predicting with genetic algorithm, the optimal process parameter configuration of the TC4 elbow for magnetic abrasive finishing was obtained as follows: the magnetic pole speed was 570 r/min, the machining gap was 2.0 mm, the diameter of the abrasive was 178 μm (80 meshes) and the feed rate was 80 mm/min. The mapping model created by the BP neural network to reflect the surface roughness of the inner surface of the TC4 elbow and the process parameters of the inner surface of the TC4 elbow has good precision, and the optimum process parameter is obtained by global optimization with genetic algorithm. It is a new method with high accuracy to optimize the processing parameters of the inner surface of TC4 elbow of magnetic abrasive finishing.
magnetic particle grinding;elbow; inner surface; surface roughness; BP neural network; genetic algorithm; TC4 titanium alloy
2019-05-30;
2019-08-29
LI Wen-long (1995—), Male, Master, Research focus: precision and special processing.
陈燕(1963—),女,博士,教授,主要研究方向为精密加工与特种加工。邮箱:laochen412@gmail.com
Corresponding author:CHEN Yan (1963—), Female, Doctor, Professor, Research focus: precision and special processing. E-mail: laochen412@ gmail.com
李文龙, 陈燕, 赵杨, 等. 采用神经网络和遗传算法优化磁粒研磨TC4弯管工艺参数[J]. 表面技术, 2020, 49(6): 330-336.
TG356.28
A
1001-3660(2020)06-0330-07
10.16490/j.cnki.issn.1001-3660.2020.06.040
2019-05-30;
2019-08-29
国家自然科学基金(51775258);辽宁省自然科学基金重点项目(20170540458);精密与特种加工教育部重点实验室基金(B201703)
Fund:Supported by National Natural Science Foundation of China (51775258); Natural Science Foundation Plan Key Projects of Liaoning Province (20170540458) and Key Laboratory Fund of Ministry of Education for Precision and Special Processing (B201703)
李文龙(1995—),男,硕士研究生,主要研究方向为精密加工与特种加工。
LI Wen-long, CHEN Yan, ZHAO Yang, et al. Optimizing technological parameters of magnetite grinding TC4 elbow by neural network and genetic algorithms[J]. Surface technology, 2020, 49(6): 330-336.
