基于NSGA-II 算法的航天产品装配公差多目标优化

施祥玲，徐小明，苏林林，徐培利，皮 刚

（上海航天设备制造总厂有限公司，上海 200245）

0 引言

公差优化设计是在确保产品制造精度、功能及性能要求的基础上，按照特定的方法以及相应的约束条件合理分配产品尺寸链中各组成零件的公差，其是决定产品的制造成本及质量等的重要因素。传统的公差优化设计主要是依据相关标准或设计人员的经验等方法确定，其研制生产过程中经常发生由于几何精度设计不合理导致零件返工、零件互换性差以及装配精度难以满足等问题，直接影响了产品的功能和性能。因此，考虑公差分配对产品生产研制成本的影响，在确保产品功能及性能实现的基础上，围绕着降低生产成本、质量损失成本进行的产品装配公差优化分配的研究具有重要意义。

针对传统的公差优化方法的不足，文献［1］以制造成本及质量损失为优化目标函数，分别采用粒子群算法（Particle Swarm Optimization，PSO）和遗传算法（GA）进行了求解，实现了公差优化设计。文献［2］利用模拟退火算法，以产品装配精度和加工成本建立目标函数，获得装配精度优化结果，能够在很大程度上提高产品装配精度。文献［3］构建了含装配成本的公差优化设计模型，利用改进的PSO，求解基于制造成本以及质量损失的装配公差多目标优化问题。文献［4］利用PSO 与层次分析法相结合的方法，对以装配性能、加工成本和装配操作复杂度为目标优化函数的公差优化设计模型进行求解。文献［5］以制造成本、质量损失及加工能力指数为优化目标函数，提出了一种多工序尺寸和公差的优化设计方法，采用目标层解法优化特征内的各个工序基本尺寸和尺寸公差，实现降低产品研制总成本的目的。文献［6］提出了一种公差优化分配方法，在综合考虑成本-公差函数、尺寸公差和形位公差之间关系的基础上，利用公差混合优化分配法和传统方法进行非线性优化分配求解。然而，仅考虑单目标优化无法满足实际装配生产中多项产品指标相互协调的决策需求，通过多个目标函数线性相加组合，该方法会由于各个优化目标函数的量纲或数量级不同，导致权重系数的分配有一定的主观性和不稳定性，无法解决Pareto 最优前沿面为非凸的问题。

文献［7］在综合考虑加工成本、质量损失成本和公差敏感性的基础上，以装配性能要求和加工能力为优化的约束条件，利用改进的PSO 进行求解，得到Pareto 最优解集。文献［8］以零件设计公差作为优化变量，以装配偏差与质量损失为优化目标，提出了一种基于NSGA-II 算法的解决公差多目标优化分配的有效方法，获得了多目标函数的最优解集。但上述方法在建立产品成本-公差模型方法上，主要考虑零件的加工成本与质量损失，未关注产品零件公差与装配成本之间的关系。

近年来，随着航天的快速发展，航天类产品呈现出批量小、结构复杂、精度要求高等特点，产品的装配操作占据了生产的大量成本支出与工时，是航天类产品研制生产过程的重要环节。装配成本也是决定航天类产品生产制造成本的一个重要指标，必须将其考虑进产品制造的成本模型中。

本文针对航天产品生产过程中装配工艺方法，在同时考虑产品零件的加工成本以及产品装配成本的基础上，提出一种航天产品成本-公差模型，建立了以产品成本与质量损失为目标的多目标公差优化设计模型，采用NSGA-II 算法对航天产品装配公差多目标优化问题进行分析求解。最后，以空间站某型号的一个部件产品的公差多目标优化为例对算法进行验证。结果表明：基于NSGA-II 算法的装配公差优化结果在满足设计功能及性能要求的前提下，可以提高产品装配公差优化分配的有效性和合理性。

1 装配公差多目标优化模型

随着我国航天事业飞速发展，航天产品呈现出结构精密、装配精度要求高等特点，导致装配占据了航天产品研制过程的大量工时和成本支出。因此，本文建立成本公差模型时引入装配成本概念，综合考虑加工成本和装配成本，同时构建产品质量损失模型，以产品质量的损失及生产制造的成本作为目标函数进行航天产品装配公差优化设计，以获得合理的公差优化设计方案，均衡公差对成本及质量损失的影响。

1.1 目标函数构建

1.1.1 成本公差模型

1）加工成本-公差模型。

加工成本基本上决定了机械产品的成本的绝大部分，而零件公差又是影响加工成本的重要因素，因此，在保证产品的装配精度及功能、性能前提下，不同的公差分配设计成为决定成本高低的重要因素。

目前，国内外学者相继提出了10 多种“成本-公差”的基本数学模型，如指数模型、幂指数模型、多项式模型以及指数和幂指数复合模型等公差模型［9］，见表1。

根据表1 中各模型的误差数据，为提高模型建立的准确性，本文采用绝对误差较小的5 次多项式模型，加工成本-公差模型为

表1 加工成本-公差模型及误差对比Tab.1 Comparisons of machining cost-tolerance models and errors

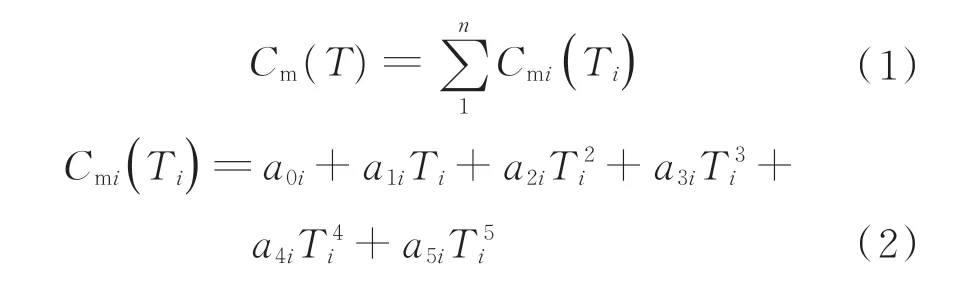
式中：Cm为总的加工成本；n为产品中尺寸公差的数目；Ti为第i个组成环的公差；Cmi为第i个组成环的公差造成的加 工成本；a0i、a1i、a2i、a3i、a4i及a5i为与公差相关的加工成本系数。

2）装配成本-公差模型。

在航天产品机构精密化、功能复杂化的发展进程中，装配已经成为航天类产品制造过程的主要环节，占据了产品研制的大部分时间。所以，装配成本也是评价航天类产品研制成本的关键指标，建立装配成本-公差模型［3］为

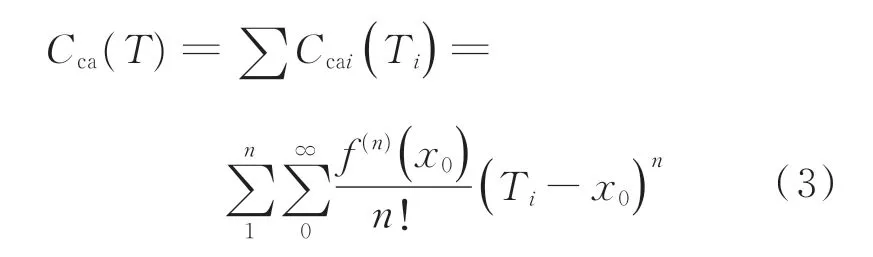
为减小计算量并提高计算精度，根据式（3），对装配成本Cai求其麦克劳林级数，则有Cai的5 次展开式为

式中：b0i、b1i、b2i、b3i、b4i及b5i为装配成本系数。

1.1.2 质量损失模型

产品研制完成交付使用或上市后由于其质量特性的波动所造成的损失表征为其质量损失［10］，最为常用的为田口二次型模型。假设某一产品的质量特征值为y，目标值为m，利用基于田口二次型质量损失函数的质量损失-公差模型，则有

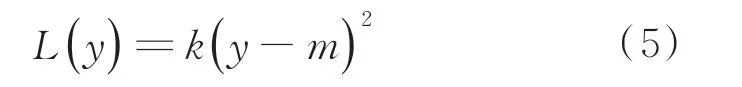
式中：k为质量损失系数，与y不相关。

将公差取双向对称分布，可得

因此，根据产品的公差尺寸可建立质量损失-公差模型为

则有产品总的质量损失成本为

1.2 约束条件建立

在公差优化研究领域，约束条件一般包括加工合格率约束、装配功能要求、装配的工艺性、工序能力指数及经济加工能力等。本文建立最常用的装配功能公差链约束和加工方法的经济性公差约束模型。

1.2.1 装配功能要求

极值法以及均方根法是传统公差设计与分析的主要方法。其中，相比于极值法，均方根法可以在确保产品的装配精度、功能及性能要求的基础上，获得更为合理的公差限。本文以均方根法作为装配性能要求计算的依据，则

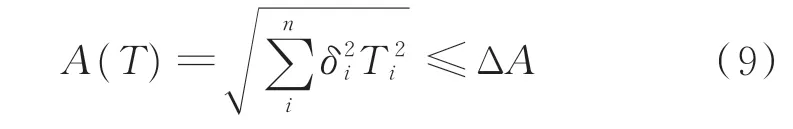
式中：δi为第i个尺寸公差的灵敏度系数；ΔA为装配功能的要求值。

1.2.2 经济加工能力

传统公差设计优化时，设计公差必须在经济加工的能力范围之内，即

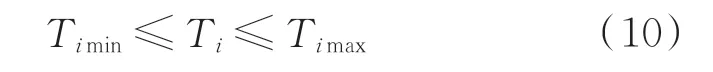
式中：Timin为第i个组成环的公差的最小加工能力公差；Timax为第i个组成环的公差的最大加工能力公差。

1.3 公差优化多目标模型

综合1.1 节及1.2 节所述，本文在考虑装配成本的前提下，以产品的制造成本以及质量损失为优化目标，以装配的功能要求及经济加工的能力为优化约束条件，可建立装配公差的优化模型如下：

式中：C（T）=Cm（T）+Ca（T）。

由于零件公差与装配成本间不存在显式的表达关系，但零件公差越小，加工所需时间越长，加工成本越大，装配工艺性越好，装配成本越小，所以，为减小计算量并确保计算精度，对同用5 次多项式构建模型的加工成本与装配成本进行量化处理，取Cmi（Ti）=ζiCai（Ti），以便公差优化设计的定量分析，ζi为与公差有关的常数。

2 基于NSGA-II 的公差多目标优化

多目标优化问题是指一个系统中的多个目标函数在相应约束条件下同时得到优化的问题，该类问题的优化结果一般为一个解集，这个解集称作Pareto 最优解或者非支配解，解集中任一解针对优化的多目标函数来说是不存在绝对的优劣。带精英策略的非支配排序遗传算法（NSGA-II 算法）［11］就是基于Pareto 最优概念的非支配排序遗传算法。该算法具有复杂度低、最优解的多样性好等优点，算法优化的主要步骤如图1 所示。

图1 NSGA-II 算法步骤Fig.1 NSGA-II procedure

针对公差多目标优化问题，基于NSGA-II 算法以各组成环的公差为决策变量=行多目标轨迹优化求解，首先，根据给定的各组成环公差随机产生一个种群大小为N的初始父代种群H0，同时通过交叉、变异的遗传算子产生一个种群大小也为N的子代种群I0；然后，汇总父代种群Ht与子代种群It，得到规模为2N的种群Rt；根据非支配排序算法将Rt种群中的全部2N个个体重新排列，得到等级F1，F2，F3，…；再根据非支配排序、拥挤度距离和约束违背值计算的排序结果选取N个个体作为新的父代种群Ht+1，通过选择、交叉及变异的遗传操作产生新的子代种群It+1，重复迭代直至最终得到满足装配功能要求和加工能力的公差Pareto 最优解。

3 实例验证

3.1 验证条件与参数设置

以空间站某型号组件为例，验证本文提出的基于NSGA-II 算法的航天产品装配公差多目标优化模型的有效性。组件三维模型如图2 所示，组成环各零件的设计公差见表2，装配尺寸链如图3 所示，其中x0为封闭环，即下平面到凸台平面的距离为（127±0.1）mm，其余为组成环。

图2 空间站某产品装配体Fig.2 Assembly of a component of the space station

表2 公差分配结果Tab.2 Tolerance distribution results

图3 装配尺寸链Fig.3 Dimension chain for assembly

3.2 仿真结果及解的选择

根据产品零件实际加工工艺方法，选用车削加工的公差-成本模型［9］建立本文加工成本-公差模型：

因质量损失系数A/4T2表征的是不同的公差对零件质量损失的成本影响大小，在优化计算过程中可将其指定为一常数，本文取为80。最后以C（T）、L（T）为优化的目标函数，装配功能要求及经济加工能力为约束条件，取装配成本系数ζ=0.35，NSGA-II算法的迭代次数设置为200，种群的数量设置为200，优化可得到成本和质量损失综合优化的Pareto 前沿面如图4 所示。由图4 可知，越靠近坐标系原点产品质量损失越大，越远离时产品生产成本越高。质量损失最优性能制约着生产成本最优性能。

为了方便在Pareto 前沿面中选择出理想的最优解，构建归一化权重目标函数如下：

式中：N1、N2是范围系数，用于将各优化目标置于统一数量级；α1、α2为权重系数，代表各优化目标的权重，可根据实际需要确定。最小化组合目标函数即可获得实际工程需要的理想最优解。

指定α1=α2=1/2，N1=100，N2=1，由式（13）求解组合目标函数fc的最小值，得到最优解C=685.530，L=1.361，得到各组成环公差见表2。

图4 公差优化的Pareto 最优解分布Fig.4 Distribution of the Pareto optimal solution of tolerance optimization

据实际加工情况，在考虑产品零部件材料的加工工艺性与零件的装配性等条件基础上，圆整得到整合后各组成环公差见表2，利用该公差进行零件机加工，与原公差比较，减少了零件的加工工时，降低了产品加工成本，提高了装配成功率，降低了质量损失，验证了本文基于NSGA-II 算法的装配公差优化方法的适用性和有效性。在航天机构产品结构越来越精密、性能要求越来越复杂、装配精度越来越高的发展背景下，本文的算法可应用在航天领域，特别在机构类产品的设计与装配阶段，为航天机构产品装配公差设计提供了有效的设计方案。

4 结束语

本文在考虑航天产品装配成本条件下，建立了一种基于成本和质量损失的装配公差多目标优化设计模型。对航天产品装配而言，提高了装配公差优化设计模型中的制造成本的可信度。利用NSGA-II 算法对装配公差的多目标优化模型进行求解，获得了均匀分布的Pareto 最优解，并构建归一化目标函数选择期望解。通过空间站某型号组件装配实例，验证了模型及优化方法的有效性以及适用性，模型方法获得的优化公差可提高装配成功率，降低产品加工成本及质量损失。在构建装配的成本模型时进行了量化处理，获得装配成本和公差的精确数学表达模型需要进一步加以研究。