基于深度学习和AMP的MIMO检测算法

朱啸豪 孙超 姜述超

摘 要：大规模多输入多输出（multiple-input multiple-output，MIMO）是5G和未来移动无线网络的关键技术之一。但是，“大规模”带来显著性能增益的同时，也给接收机设计带来了挑战。基于深度学习和近似信息传递（approximate message passing，AMP）检测算法，提出了一种新的深度学习网络AMP-net，用于MIMO检测。在提出的算法中，将AMP算法的每一次迭代作为单层网络的基础架构，同时加入非线性神经单元及可训练权重系数，以实现在固定网络层数时得到更低的误码率。仿真结果证明，对比迭代次数为L的AMP算法，网络层数也为L的AMP-net可以得到较低的误码率，但和无限迭代的AMP算法还是有差距。同时也讨论了可训练的阈值函数对AMP-net的影响。仿真结果证明，使用一个小的全连接网络来作为阈值函数，比较其余阈值函数可以得到更低的误码率。

关键词：大规模MIMO;深度神经网络;5G;信号检测

Abstract：Massive multiple-input multiple-output （MIMO） is one of the key technologies for 5G and future mobile wireless networks. However， "large scale" brings significant performance gains， but also poses challenges for receiver design. Based on deep learning and AMP （approximate message passing） detection algorithms， this paper proposes a new deep learning network AMP-net for MIMO detection. In the algorithm， each iteration of the AMP algorithm is used as the infrastructure of the single-layer network， and the nonlinear neural unit and the trainable weight coefficient are added to achieve a lower error rate when the network layer is fixed. The simulation results show that comparing the AMP algorithm with the number of iterations L， the AMP-net with the network layer number L can get a lower bit error rate， but there is still a gap between the AMP algorithm of infinite iteration. At the same time， we also discuss the impact of the trainable threshold function on AMP-net. The simulation results show that using a small fully connected network as the threshold function can achieve a lower bit error rate compared with the remaining threshold functions.

Key words：massive MIMO;deep neural network;5G;signal detection

0 引言

与第四代（4G）无线网络相比，第五代（5G）无线网络的数据速率有望提高约1 000倍[1]。 高频谱效率和足够的空间自由度使大规模多输入多输出（MIMO）成为5G和未来移动无线网络的关键技术之一。但是，大规模MIMO面臨许多挑战，特别是在接收器的检测方面[2]。尽管最大似然（maximum likelihood， ML）检测算法可以获得最低的误码率（bit error rate，BER），但是随着天线数量的增加，计算复杂度也随之增加。例如，对于一个具有64个发射天线的MIMO系统，使用BPSK调制，ML检测算法需要经过检索1.84×1019个不同的情况才能获得最佳检测结果。传统的线性检测算法，例如迫零（zero-forcing， ZF）检测和线性最小均方误差（linear minimum mean square error， LMMSE）检测算法，具有较低的复杂度，但其获得的BER与ML算法之间存在较大差距。更高级的检测器包括决策反馈均衡（decision feedback equalization，DFE），近似消息传递（AMP）[3]和半确定松弛（semidefinite relaxation，SDR）[4-5]，在许多实际情况下，AMP和SDR均可提供接近最佳的精度，并且AMP在实践中实现简单。

近年来，深度学习在计算机视觉和自然语言除了等领域取得了成功的应用，也有部分学者开始研究在通信上应用深度学习，这些网络通常是具有许多非线性操作单元和层的神经网络。有一种设计深层架构的有前途的方法是展开现有的迭代算法[6]。每次迭代都被视为一个层，这种迭代算法就变成了一个网络。

本文将传统的AMP迭代检测算法与深度学习相结合，提出了一种新的深度学习网络AMP-net，用于MIMO检测。传统的AMP算法在不同信噪比和不同信道时，迭代至收敛的次数不一致。在本文提出的算法中，将AMP算法的每一次迭代作为单层网络的基础架构，同时加入非线性神经单元及可训练权重系数，以实现在固定网络层数时得到更低的误码率。仿真结果表明，对比迭代次数为L的AMP算法，网络层数也为L的AMP-net可以得到较低的误码率，但和无限迭代的AMP算法还是有差距。同时本文也讨论了可训练的阈值函数对AMP-net的影响，仿真结果表明，使用一个小的全连接网络来作为阈值函数，对比其余阈值函数可以得到更低的误码率。

論文接下来将首先介绍大规模MIMO的系统模型;然后在第2部分简单介绍AMP检测算法，第3部分基于AMP算法和深度学习提出了AMP-net架构;在第4部分，对AMP-net和不同阈值函数进行了仿真分析;最后进行总结。

1 大规模MIMO系统模型

在上行链路中，一个大规模MIMO系统一般由具有Nr个天线的基站（base station， BS）和Nt个单天线用户组成。系统原型如图1所示。

此外，为了进一步提高AMP-net的性能，受ResNet[9]启发，引入了残差的概念，其中每一层的输出是与前一层输出的加权平均值。

4 仿真结果

此部分通过仿真实验验证所提出的算法的优异性能，仿真场景如下：

收发天线数：Nr=Nt=32，

训练集信噪比：5-15 dB，

测试集信噪比：0-16 dB。

仿真中使用Adam Optimizer[10]优化神经网络。在每次迭代中使用5 000个随机数据样本进行批处理训练，并对网络进行50 000次迭代训练。每个样本是根据x，H和噪声的统计从（1）独立生成的。关于噪声，其方差是未知的，因此也是随机产生的，因此SNR将均匀地分布在U（SNRmin，SNRmax）上。这种方法使本文提出的算法能够检测更加广泛的SNR值，如图3所示。

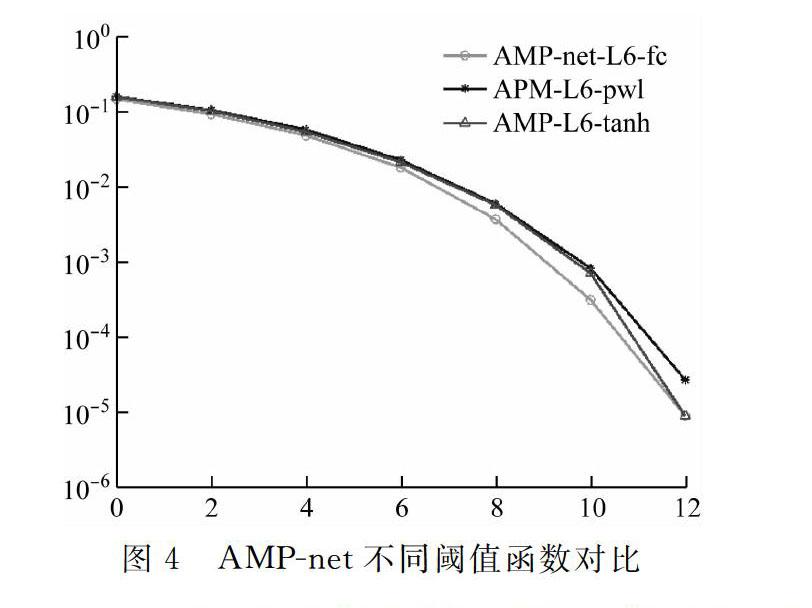
图3展示了在不同收发天线数量的情况下，6层AMP-net比6次迭代的AMP算法对比，误码率为10-3时信噪比提高了1.7 dB，与无限迭代直至收敛的AMP算法只落后1 dB，如图4所示。

图4是L=6时，不同阈值函数的AMP-net对比。结果说明采用一个全连接网络作为阈值函数可以达到更好的检测效果，误码率为10-3时比其余阈值函数提高至少0.5 dB。

5 总结

本文基于深度学习和AMP检测算法提出了AMP-net网络架构，对比同样迭代次数的AMP算法，检测效果有显著提高，且可预见的是可以通过改善网络结构和阈值函数进一步提高算法性能。鉴于提出这种结构的思路，传统的迭代检测算法都可以展开成深度神经网络，这给当下检测算法和深度学习网络架构的研究提供了一个新的思路。这也将是我们未来的工作。

参考文献

[1] Andrews-J-G.， Buzzi-S.， Choi-W. What will 5G be？. IEEE Journal on selected areas in communications， 2014，32（6）， 1065-1082.

[2] E G Larsson. MIMO detection methods：How they work[J]. IEEE Signal Process. Mag.， 2009，26（3）：91-95.

[3] C Jeon， R Ghods， A Maleki， et al. Optimality of large mimo detection via approximate message passing[C]// IEEE International Symposium on Information Theory （ISIT）. IEEE， 2015：1227-1231.

[4] Z Q Luo， W K Ma， A M So， et al. Semidefinite relaxation of quadratic optimization problems[J]. IEEE Signal Processing Magazine， 2010， 27（3）：20-34.

[5] J Jalden， B Ottersten. The diversity order of the semide？nite relaxation detector[J]. IEEE Transactions on Information Theory，2008，54（4）：1406-1422.

[6] J R Hershey， J L Roux， F Weninger. Deep unfolding：Model-based inspiration of novel deep architectures[J]. arXiv preprint arXiv：1409.2574， 2014.

[7] Senel K， Larsson E G. Device activity and embedded information bit detection using AMP in massive MIMO[J]. arXiv preprint arXiv：1709.05161， 2017.

[8] Donoho D L， Maleki A， Montanari A. Message-passing algorithms for compressed sensing[J]. Proceedings of the National Academy of Sciences of the United States of America， 2009， 106（45）：18914.

[9] K. He， X Zhang， S Ren， et al. Deep residual learning for image recognition[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition， 2016：770-778.

[10] Kingma-D-P， Ba-J. Adam：A Method for Stochastic Optimization. international conference on learning representations， 2015.

（收稿日期：2019.11.14）