基于RBF-PID控制器的液压伺服振动台波形复现研究

付艳娟

摘 要：为解决液压伺服振动台运行过程中系统非线性环节和外部负载扰动较大的难题，设计一种将RBF神经网络和PID控制器相结合的控制策略。在分析液压振动台数学模型和控制器结构的基础上，利用RBF神经网络良好的非线性映射能力，实现PID控制器参数的在线调整。与经典PID控制器相比，所提控制策略具有较好的跟踪能力和鲁棒性。

关键词：液压伺服振动台;RBF神经网络;PID控制器;波形复现

0引言

液压伺服振动台具有力重比高，负载刚度大和响应快速等优点，常用于模拟航空航天、汽车制造和民用建筑等领域的振动环境[1]。液压伺服系统的强非线性特性，如伺服阀压力流量非线性、执行器摩擦非线性和环境干扰等非线性，严重制约了经典PID控制器的控制性能。针对传统PID控制器无法解决时变非线性扰动的缺点，本文采用RBF神经网络来实时调整PID控制器的参数，以确保液压振动台能够准确复现给定波形。

1系统组成和数学模型的建立

液压伺服振动台的控制原理图如图1所示，主要有伺服放大器、电液伺服阀、液压缸和位移传感器组成。当控制指令信号电压作用于系统时，液压缸便产生位移，输出位移经过位移传感器转化为反馈电压，与指令信号电压比较后，得到偏差信号电压。偏差信号经伺服放大器、电液伺服阀传到液压缸活塞上，使输出位移向着减小偏差的方向变化，直到输出位移等于指令电压所对应的值为止[2]。

式中，为负载流量;为阀芯位移;为负载压力;为流量增益;为流量压力系数，为活塞面积;为活塞位移;为液压缸两腔的总容积;为总的泄露系数; 为油液的弹性模量，为活塞上的总质量;为粘性阻尼系数;k为负载弹簧刚度;为活塞上的任意外负载力。

由式（4）可以看出液压伺服振动台的响应波形和液压缸的活塞位移有关，活塞位移量可以通过控制计算机的电压信号实现。但是振动台运行过程中的非线性扰动和模型物理参数的变化，使得其输出响应不能很好地复现给定的输入波形，这里采用RBF神经网络和PID控制器相结合的方法来实时调整控制器的参数，提高控制系统的控制精度。

2 RBF-PID控制器的设计

在液压伺服振动台控制系统中，一般采用增量式PID控制器[3]。为了使振动台能够准确复现给定的波形，假设液压缸活塞所要得到的位移量为，而实际位移量为，则测量误差为。PID控制器的三项输入分别为，，。

振动台实际运行中，液压伺服系统内部的参数会有所摄动，固定参数的PID控制器无法克服外界的扰动而得到稳定的状态，情况严重时可能导致系统超调[4]。因此采用RBF神经网络来调节PID控制器的参数，其控制结构如图2所示。

RBF神经网络具有输入层、隐含层和输出层三层结构的前馈网络，从输入层空间到隐含层空间的变化是非线性的，而从隐含层空间到输出层空间的变换是线性的。将PID控制器的三个参数作为输入层，神经元作为隐含层，控制器参数的雅克比信息可从RBF神经网络中获得[5]。

输入层取为，隐含层的激励函数为，为第个基函数的中心点，是自由参数，它决定基函数围绕中心点的宽度。输出层为，为高斯函数的输出，为隐含层至输出层的网络权值。

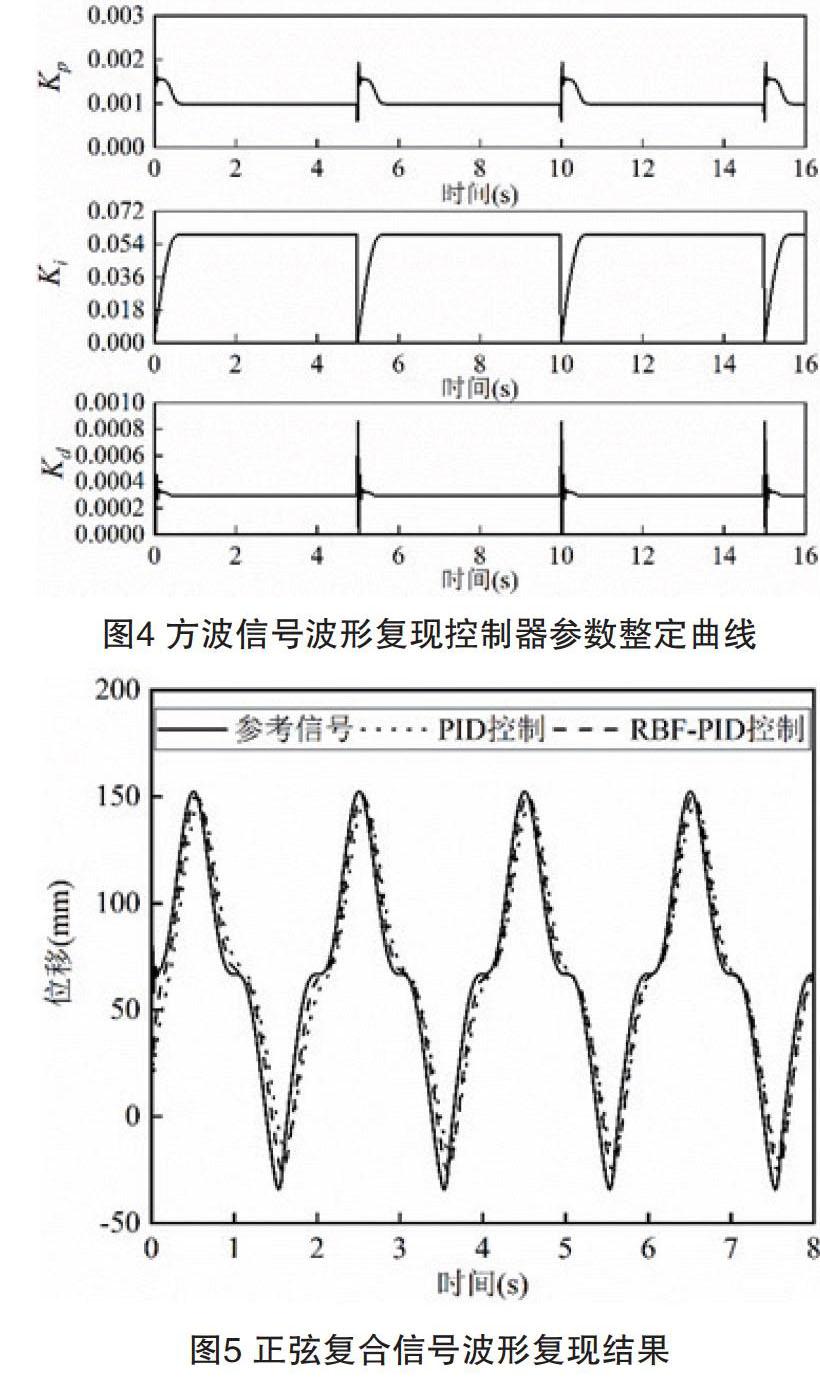
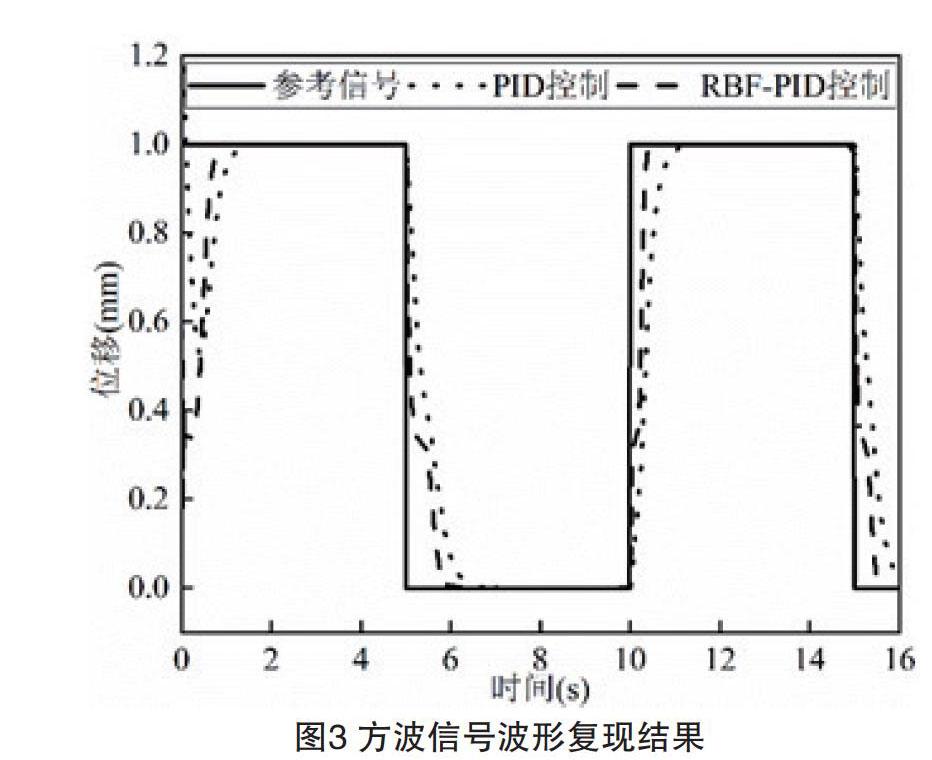
為了验证所提控制策略的跟踪性能，分别比较PID控制器和RBF-PID控制器控制下阶跃信号和正弦复合信号的波形复现精度。图3和图4分别给出了所提控制器对方波信号的复现结果和控制器参数的整定结果，其中方波信号的幅值和周期分别设定为1mm和5s。从图3和图4可以看出RBF-PID控制器具有较好的响应速率和跟踪精度，且控制器参数随着参考信号的变化迅速收敛到稳定状态。图5正弦复合信号波形复现结果，从图5可以看出RBF-PID控制器与PID控制器相比具有更好的波形复现精度。上述仿真结果表明设计的RBF-PID控制器能够较好跟踪给定曲线，削弱系统非线性参数的影响。

4结语

针对液压伺服振动台的波形复现问题，设计了一种RBF-PID控制器，充分利用RBF神经网络动态整定PID控制器的参数，削弱系统非线性参数所带来的不利影响。仿真结果表明所提控制策略可以克服液压系统的非线性影响，且具有快速响应、抗外部干扰的控制效果。

参考文献

[1] 梁利华.液压传动与电液伺服系统[M].哈尔滨：哈尔滨工程大学出版社，2005.

[2] 刘爽，李硕，赵丁选，等.主动油气悬架电液伺服系统的自适应滑模控制[J].燕山大学学报，2019，43（6）：477-484.

[3] 刘金琨.先进PID控制MATLAB仿真[M].北京：北京电子工业出版社，2004.

[4] 何禹锟，高强，侯远龙.某定深电液伺服系统的粒子群优化神经网络PID控制[J].兵工自动化，2019，38（11）：24-28.

[5] Essa Mohamed，El-Sayed M，Aboelela，et al.Model predictive force control of hardware implementation for electro-hydraulic servo system[J].Transactions of the Institute of Measurement and Control，2019，41（5）：1435-1446.