有杆抽油泵固定凡尔球开启时间规律研究*

王小兵 吕雷纲 李森 边斌 刘阳 龚浩宇 王多琦

(1.常州大学石油工程学院 江苏常州 213164; 2.Biological and Environmental Sciences and Engineering (BESE) Division, Water Desalination and Reuse Center (WDRC), King Abdullah University of Science and Technology, Thuwal 23955-6900, Kingdom of Saudi Arabia)

0 引言

我国机械采油井数已超过90%以上，其中有杆抽油井占总机械采油井数的90%以上，有杆泵抽油从出现至今一直是应用最广泛的人工举升方法[1]。有杆抽油泵固定凡尔球的打开程度影响泵的吸入过程，固定凡尔球达到最大打开程度及其所需开启时间的长短对流体进泵效率有直接的影响。

关于抽油泵固定凡尔球运动规律的研究中，实验[2-3]得到了固定凡尔球的实际运动规律但理论结果较少；数值模拟研究基于国内外专家学者[4-14]的不断优化取得了非常大的进展。本文主要弥补数值模拟研究中以UDF编程结合流体力学模型控制固定凡尔球运动规律的缺陷，建立流固耦合模型，实现了固定凡尔球在只有轴向位移条件下的自由移动，解决了运动过程中凡尔球与其他壁面产生接触的网格变化、固体相互作用力问题，得到了各影响因素下固定凡尔球打开程度与开启时间的变化规律曲线，从而为抽油机工作制度中部分参数的合理优化提供理论参考。

1 模型的建立

研究采用的固定凡尔模型为外径70 mm的管式泵，将固定凡尔在上冲程阶段的柱塞简化为指定位移的固体域。因上冲程游动凡尔处于关闭状态则柱塞的几何结构为矩形且不考虑其与油管壁的配合间隙。在模型建立之前提出以下几点假设：

(1)凡尔球只有轴向运动，不考虑自转、公转等因素。

(2)模型中柱塞不存在漏失，且不考虑间隙。

(3)泵内流体不含气体，且高含水。

(4)泵筒无倾斜，凡尔球所受重力垂直向下。

1.1 模型的控制方程

固定凡尔球的流固耦合模型包含流体流动模型的控制方程和固体力学模型的控制方程。

固体力学在研究线弹性体时，其控制方程为：

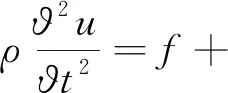
(1)

式中，ρ为质量密度，kg/m3；u为位移矢量，m/s；f为单位体积力，N；σ为应力，Pa。

对于线弹性材料，固体力学基于胡克定律将应力张量与弹性应变张量联系起来的方程为：

σ=σex+C∶εel=σex+C∶(ε-εinel)

(2)

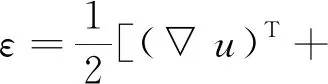
(3)

C=C(e,v)

(4)

式中，C为弹性张量，εel为总应变ε与非弹性应变εinel的差值，σex表示其他应力。

流体的流动模型依据雷诺数进行划分，其计算公式为：

(5)

式中，μ为动力粘度，mPa·s；ρ为密度，kg/m3；U为速度，m/s；L为管道直径，m。

通过计算雷诺数确定流体流态为湍流并建立k-ε湍流模型，其控制方程为：

(6)

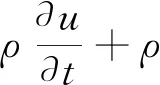
(7)

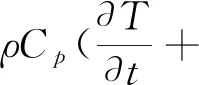
(8)

1.2 初始、边界条件

在此模型中不考虑抽油杆振动的影响，柱塞位移即悬点位移，其方程为：

(9)

式中，z为泵位移，m；S为冲程，m；t为运动时间，s；T0为运动周期，r/min。

初始状态下固定凡尔球与球座给定一段距离，使其在只受重力的情况下落在球座上，时间控制函数：(t[1/s]>0)；另外，设置时间步为(-t0，Δt，t1)，则在开始计算之前的t0时间段内使固定凡尔球落于球座上；在t=0时入口压力边界上添加阶跃函数以解决压力突变造成计算的不收敛，曲线的平滑时间处理为0.01 s。

1.3 接触边界及接触压力方法

首先，定义节点中创建接触对子节点，并选择固定凡尔球边界为源边界，球座和球罩与固定凡尔球接触的边界为目标边界；其次，在固体力学模块中创建接触子节点并选中创建的接触对。在接触子节点中，考虑流固耦合中流体域网格的大变形情况，接触压力方法选择罚函数法，特征刚度为默认值：solid.Eequ，即等效材料的杨氏模量；再调整壁面之间的偏移距离，通过重复计算优化调整偏移距离为5 μm。

1.4 动网格技术

固定凡尔球运动时必须使用动网格技术计算边界的运动或变形问题，为此在模型中添加动网格。在动网格节点下，添加变形域节点以指定选定域的形状由域边界控制，网格平滑类型选择Yeoh(更易于收敛)；添加固定边界节点以指定选定边界保持其形状且不移动；添加指定网格位移节点以完全指定空间网格对于边界处网格的位移。

2 结果分析

抽油机工作制度的调整是改变冲次、冲程、泵径以及下泵深度，其中下泵深度影响泵的入口压力；另外流体粘度、柱塞的漏失以及流体的压缩性也会影响流体对固定凡尔球的作用力。因本文研究外径为70 mm的抽油泵固定凡尔，不考虑柱塞的漏失问题，且针对高含水的油井而不考虑气体膨胀的影响，因此分析冲次、冲程、流体粘度和入口压力的影响规律。首先计算出固定凡尔球的运动规律，进而对数据进行后处理得到固定凡尔球打开程度与所需开启时间的变化规律，研究得到了各影响因素下固定凡尔球的运动规律、泵内流体速度变化规律、固定凡尔球开启时间变化规律。计算的相关参数如表1所示。

在进行研究分析之前，首先在模型中计算出固定凡尔球落在球座上关闭状态的初始位置，因为构建几何模型时不能将固定凡尔球与球座设置为接触关系，不然流体域的网格被隔断，动网格无法进行重新划分。初始位置的确定分两个步骤：首先对柱塞位移、出入口压力的边界条件乘以时间控制函数：(t[1/s]>0)(在计算时间达到0 s 之前，柱塞不移动，出入口压力为零)；其次，确定出凡尔球关闭吸入口的时间，因几何模型中凡尔球与密封圈的距离较短，为保证泵腔内的流体在凡尔球关闭过程完成后处于静止状态，时间步长适当延长，经过反复的测验以及对结果的观察之后，将时间步长设置为(-1,0.1,0)。

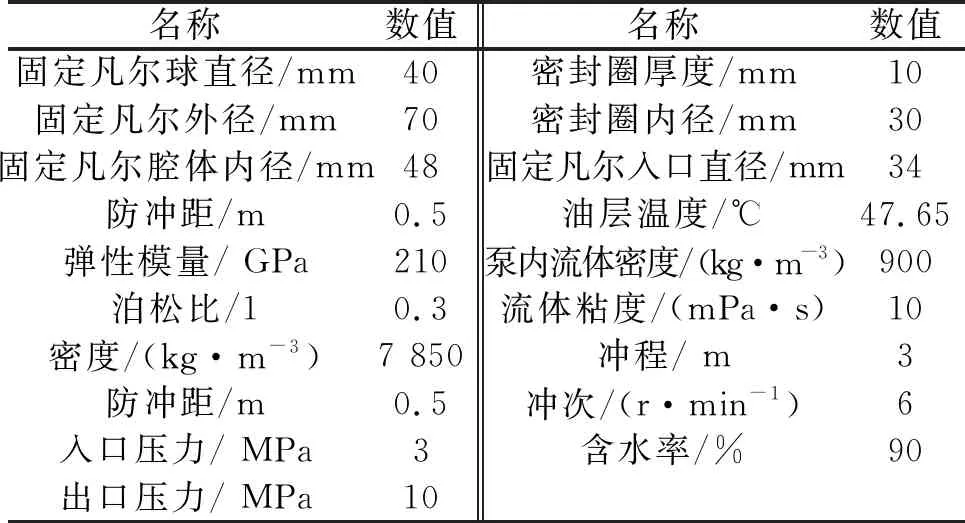
表1 计算参数表

固定凡尔球在只受重力的情况，其位移规律如图1所示。

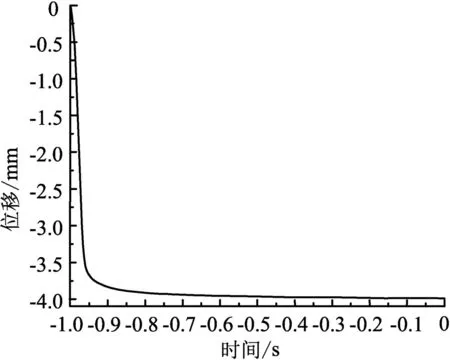
图1 固定凡尔球关闭过程的位移规律

由图1可知，固定凡尔球在只受重力的条件下，从预置位置快速向下移动，与球座接触后停止移动并关闭吸入口；关闭过程在1 s之内完成。

2.1 冲次对固定凡尔球开启时间的影响

在模型参数中改变冲次为2，4，6，8，10 r/min，将各冲次下固定凡尔球运动曲线数据导出，通过固定凡尔球的升程计算出固定凡尔球的打开程度，并利用Excel制作为固定凡尔球打开程度与开启时间数据表，最后使用Origin绘图软件得到固定凡尔球开启时间变化规律曲线，如图2所示。

由图2可知，冲次越高固定凡尔球的打开程度越大，所需的开启时间越短；冲次为2 r/min时，最大打开程度为0.2，所需开启时间为7.46 s；冲次为4 r/min时，最大打开程度为0.31，所需开启时间为3.80 s；冲次为6 r/min时，最大打开程度为0.36，所需开启时间为2.2 s；冲次为8 r/min时，最大打开程度为0.36，所需开启时间为1.70 s；冲次为10 r/min时，最大打开程度为0.45，所需开启时间为1.26 s；冲次由2 r/min增加到10 r/min时，固定凡尔球最大打开程度由0.2增加到0.45，开启时间由7.46 s减小至1.26 s。

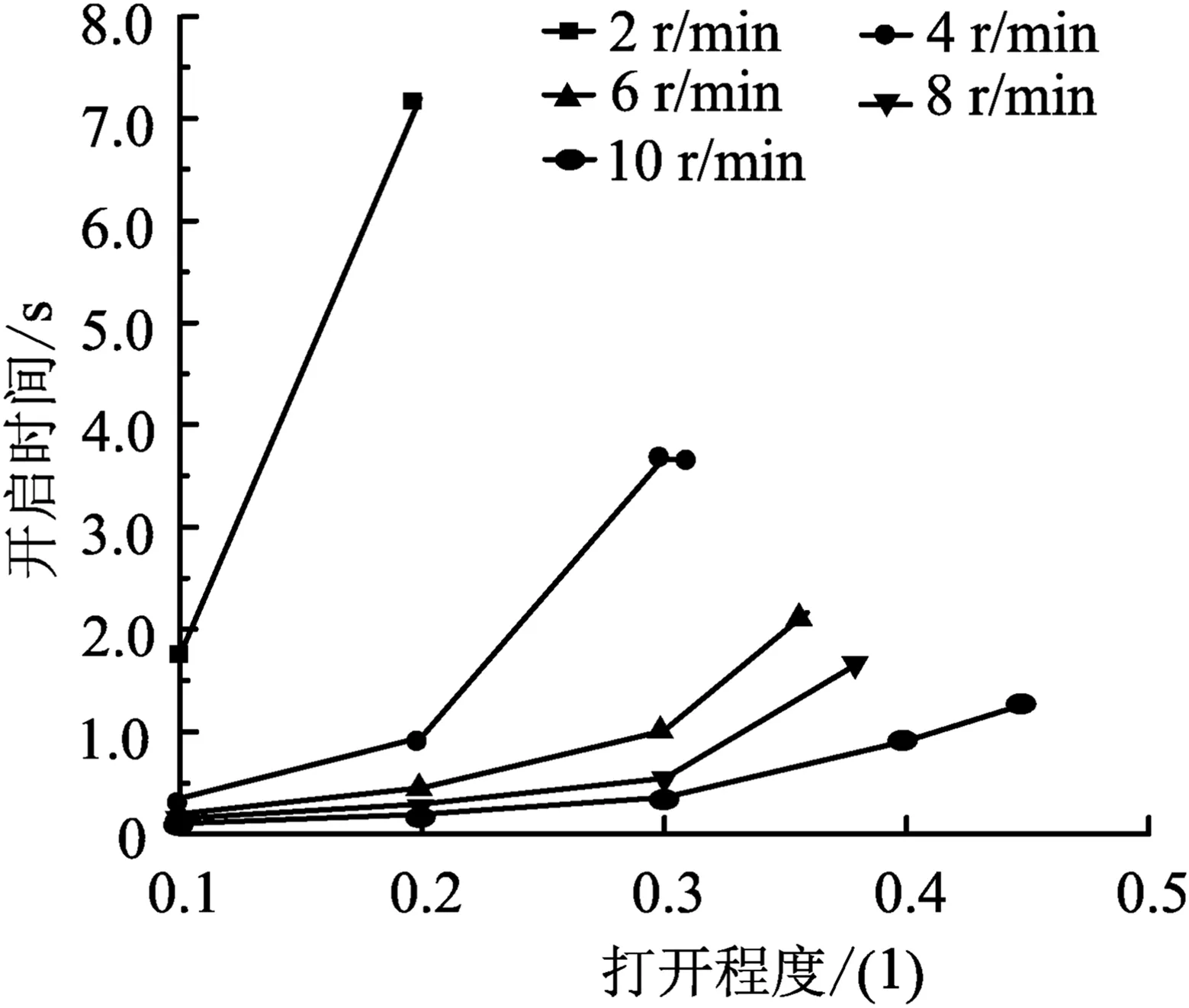
图2 冲次对固定凡尔球开启时间的影响规律

2.2 冲程对固定凡尔球开启时间的影响

在模型参数中改变冲程为1，2，3，4，5 m，将各冲程下固定凡尔球运动曲线数据导出，通过固定凡尔球的升程计算出固定凡尔球的打开程度，并利用Excel制作为固定凡尔球打开程度与开启时间数据表，最后使用Origin绘图软件得到固定凡尔球开启时间变化规律曲线，如图3所示。

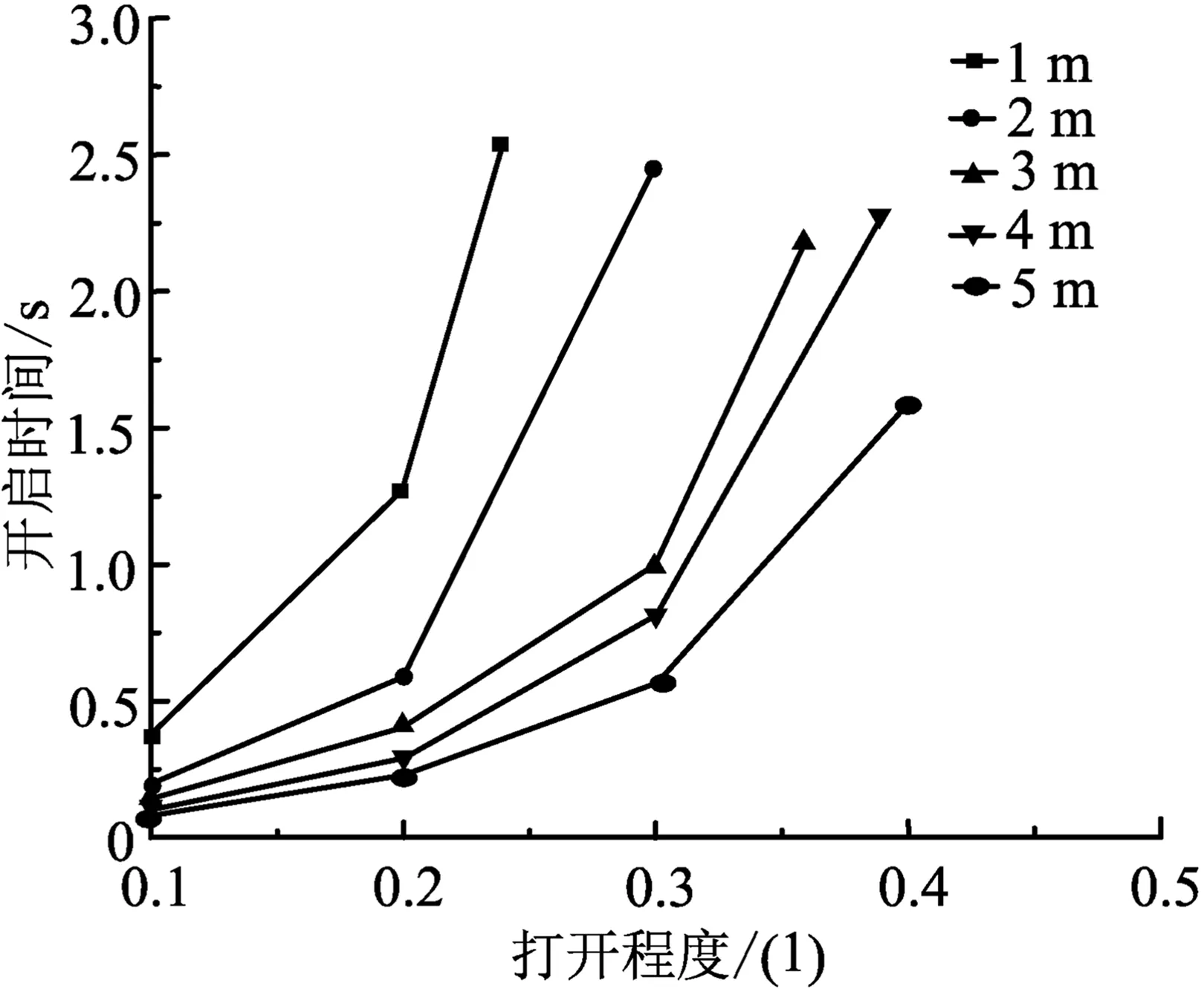
图3 冲程对固定凡尔球开启时间的影响规律

由图3可知，冲程越长固定凡尔球的打开程度越大，所需的开启时间越短；冲程为1 m时，最大打开程度为0.24，所需开启时间为2.56 s；冲程为2 m时，最大打开程度为0.3，所需开启时间为2.48 s；冲程为3 m时，最大打开程度为0.36，所需开启时间为2.20 s；冲程为4 m时，最大打开程度为0.39，所需开启时间为2.30 s；冲程为5 m时，最大打开程度为0.4，所需开启时间为1.60 s；冲程由1 m增加到5 m时，固定凡尔球最大打开程度由0.24增加到0.4，开启时间由2.56 s减小到1.60 s。

2.3 入口压力对固定凡尔球开启时间的影响

在模型参数中改变入口压力为1，2，3，4，5 MPa，将各流体粘度下固定凡尔球运动曲线数据导出，通过升程计算固定凡尔球的打开程度，并利用Excel制作为固定凡尔球打开程度与开启时间数据表，最后使用Origin绘图软件得到固定凡尔球开启时间变化规律曲线，如图4所示。

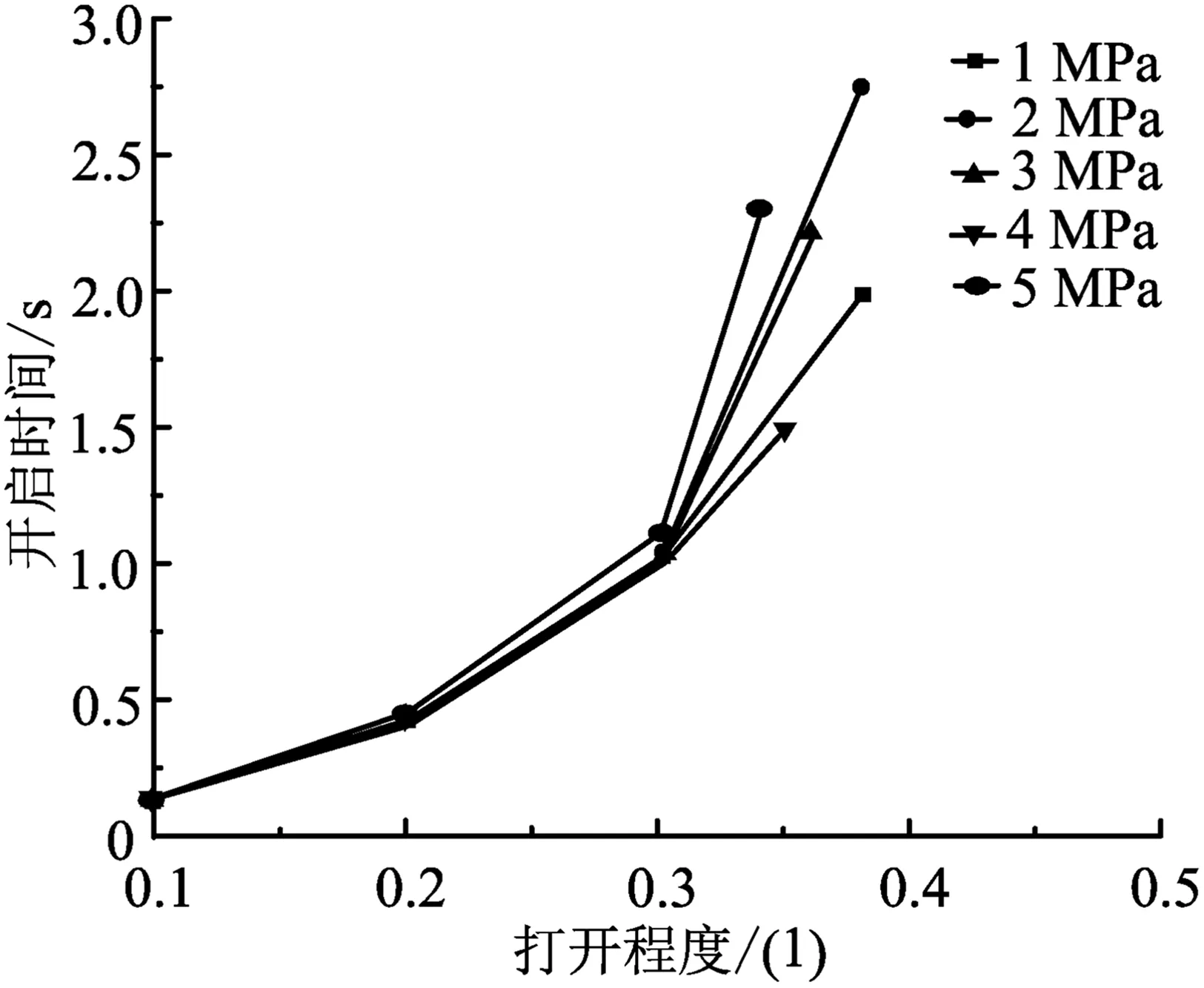
图4 入口压力对固定凡尔球开启时间的影响规律

由图4可知，入口压力为1 MPa和2 MPa时固定凡尔球的打开程度较大，其中入口压力为1 MPa时所需开启时间较短；入口压力为1 MPa时，最大打开程度为0.38，所需开启时间为1.99 s；入口压力为2 MPa时，最大打开程度为0.38，所需开启时间为0.76 s；入口压力为3 MPa时，最大打开程度为0.36，所需开启时间为2.20 s；入口压力为4 MPa时，最大打开程度为0.35，所需开启时间为1.50 s；入口压力为5 MPa时，最大打开程度为0.34，所需开启时间为2.30 s；入口压力由1 MPa增加到5 MPa时，固定凡尔球的最大打开程度在0.35左右波动，其中1 MPa时固定凡尔球打开程度最大，4 MPa时开启时间最短。

2.4 流体粘度对固定凡尔球开启时间的影响

在模型参数中改变流体粘度为10，30，50，70，90 mPa·s，以及计算得出固定凡尔球完全打开的临界粘度54 mPa·s，将各流体粘度下固定凡尔球运动曲线数据导出，通过升程计算固定凡尔球的打开程度，并利用Excel制作为固定凡尔球打开程度与开启时间数据表，最后使用Origin绘图软件得到固定凡尔球开启时间变化规律曲线，如图5所示。

由图5可知，流体粘度越高固定凡尔球的打开程度越大，所需开启时间越短，其中粘度大于54 mPa·s时固定凡尔球完全打开；流体粘度10 mPa·s时，最大打开程度为0.36，所需开启时间为2.20 s；流体粘度为30 mPa·s时，最大打开程度为0.37，所需开启时间为2.16 s；流体粘度为50 mPa·s时，最大打开程度为0.4，所需开启时间为1.92 s；流体粘度为54 mPa·s时，固定凡尔球完全打开，打开程度为1.0所需开启时间为1.86 s；流体粘度为70 mPa·s时，固定凡尔球完全打开，打开程度为1.0所需开启时间为1.24 s；流体粘度为90 mPa·s时，固定凡尔球完全打开，打开程度为1.0所需开启时间为0.94 s；流体粘度由10 mPa·s增加到90 mPa·s时，固定凡尔球最大打开程度由0.36增加到1.0的阶段，开启时间由2.20 s减小到0.94 s。

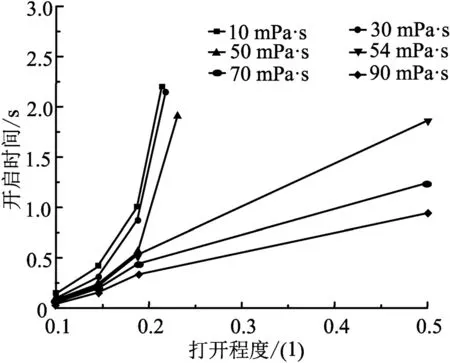
图5 流体粘度对固定凡尔球开启时间的影响规律

3 结论

(1)基于COMSOL Multiphyscis软件建立抽油泵固定凡尔球的流固耦合模型，使用时间条件和阶跃函数解决了固定凡尔球速度为零时计算不收敛的问题；运用动网格技术、自动重新划分网格、接触压力方法解决了凡尔球在流体域中移动、与球罩接触的网格问题和固体作用力的传递问题。

(2)冲次越高、冲程越长、流体粘度越大，固定凡尔球的打开程度越大、达到最大打开程度所需的开启时间越短；入口压力对固定凡尔球打开程度的影响为非线性，入口压力为1 MPa和2 MPa时固定凡尔球的打开程度较大，其中入口压力为1 MPa时固定凡尔球达到最大打开程度所需的开启时间较短。在研究范围内，流体粘度是固定凡尔球打开程度为1.0且最终完全打开的唯一影响因素，且粘度增大到一定数值时固定凡尔球的打开程度直接达到1.0且最终完全打开，悬浮在球罩处。

(3)冲次由2 r/min增加到10 r/min时，固定凡尔球最大打开程度由0.2增加到0.5，开启时间由7.46 s减小至1.26 s；冲程由1 m增加到5 m时，固定凡尔球最大打开程度由0.24增加到0.4，开启时间由2.56 s减小到1.60 s；入口压力由1 MPa增加到5 MPa时，固定凡尔球的最大打开程度在0.35左右波动，其中1 MPa时固定凡尔球打开程度最大、4 MPa时开启时间最短；流体粘度由10 mPa·s增加到90 mPa·s时，固定凡尔球最大打开程度由0.36增加到1.0，开启时间由2.20 s减小到0.94 s。

(4)合理的抽油泵工作制度不仅能节约能源消耗、降低井下维修的次数，更有利于油田安全生产与绿色环保，本文的研究结果为生产实践提供了理论参考。