多时间窗的物流配送中心-配送路径选取模型研究
2020-06-29
重庆市市政设计研究院
0 引 言
正确选择物流节点和配送服务方式,合理确定物流配送流程,对提升物流效率、提高物流企业经济效益有着非常重要的意义。罗耀波等[1]在考虑仓库容量约束和车辆容量约束的基础上,结合送取货一体化的配送模式和客户服务时间要求,建立带退货和软时间窗的多仓库选址-路径问题数学模型。Wu等[2]考虑多场站情景,将原问题分为两个子问题,运用模拟退火算法和迭代的方式进行求解。刘虹等[3]研究带时间窗约束的越库选址-路径问题,采用时间窗模糊化处理方法定义客户满意度函数,在能力和载重等约束下,建立多目标规划模型。Koç等[4]考虑带有时间窗约束的多车型选址-路径问题,提出混合整数规划模型与一组有效不等式。罗耀波等[5]针对带仓库容量约束和路径容量约束的选址-路径问题,提出一种结合模拟退火算法的混合遗传算法进行整体求解。Winkenbach等[6]将城市物流过程中货物整合、配送外包、运输方式选择等因素考虑在两级网络选址-路径问题中,构建带时间约束的混合整数线性规划模型。Pichka等[7]研究含有开放路径的两级网络选址-路径问题,提出混合整数规划模型与混合启发式算法。
以上研究,都未考虑配送中心开放成本与多时间窗口。本文在综合考虑配送中心选址、配送中心开放成本、配送车辆使用成本、服务时效需求等因素的基础上,引入配送时间窗口,即要求配送车辆仅能在规定时间窗内到达客户点,且在时间窗关闭前驶离客户点,并以总成本最小化为目标,建立多时间窗的多配送中心选址-配送路径选取模型,并利用商业化运算软件Cplex(版本12.4)对模型进行精确求解。
1 问题及数学模型
1.1 问题描述
问题具体特征如下:
(1)运输网络中包含两类节点:配送中心及配送中心辐射范围内若干有配送需求的客户点。所有节点的位置已知,配送中心是否开放需结合配送中心开放成本、配送距离、客户点需求等各种因素综合权衡而定。配送中心是配送卡车的始发/终到点。
(2)每一个配送中心均保有足够数量的配送卡车,车辆类型相同,且其额定载重、行驶速度等均为已知。
(3)客户点的货物需求已知且不可拆分,每个客户点只能由一辆配送卡车服务,且只能被服务一次。
(4)所有客户点均有服务时间窗限制,每个客户点有多个时间窗,对于每个客户点,其服务时间窗之间相互不重叠。配送卡车对客户点的服务必须在相应的时间窗开启后才能开始,在时间窗关闭前完成服务,即配送卡车不能在非时间窗的时间段到达客户点。
1.2 参数及变量
上述问题所涉及参数及变量含义如表1所示。
1.3 目标函数

目标函数为总成本最小化,目标函数式(1)包含三部分:第一部分为配送卡车的行驶成本;第二部分为配送卡车的使用成本;第三部分为配送中心的开放成本。

表1 参数及变量
1.4 约束条件
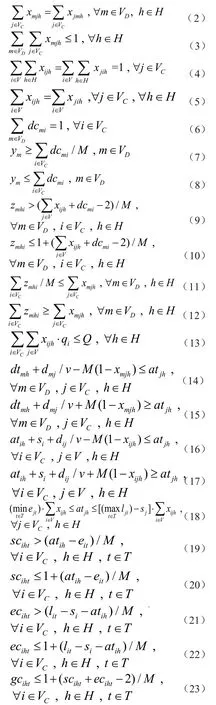

约束(2)表示配送卡车进出配送中心次数相同。约束(3)表示对于任意车辆只能使用一次。约束(4)表示对于任一客户点,只能被一辆配送卡车服务一次。约束(5)表示配送卡车进出节点次数相等,且每辆配送卡车对同一节点服务一次。约束(6)表示客户点货物由某个配送中心进行配送。约束(7)和(8)表示某配送中心是否开放。约束(9)和(10)确定变量zmhi的取值,表示客户点货物由某辆配送卡车从某配送中心进行配送。约束(11)和(12)表示若配送中心下的配送卡车被使用,则该配送卡车一定从该配送中心出发。约束(13)表示配送卡车载重限制。约束(14)和(15)表示配送卡车从配送中心到客户点的时间连续性。约束(16)和(17)表示配送卡车在客户点间的到达时间连续性。约束(18)表示配送卡车到达客户点的基本时间约束,并对未使用配送卡车进行取值的辅助约束。约束(19)和(20)确定变量sciht的取值,表示配送卡车在客户点某个时间窗开启后到达。约束(21)和(22)确定变量eciht的取值,表示配送卡车在客户点某个时间窗关闭前到达。约束(23)和(24)确定变量gciht的取值,表示配送卡车在哪个时间窗到达客户点。约束(25)表示配送卡车到达客户点的时间约束。约束(26)和(27)表示配送卡车离开客户点的时间限制,即配送卡车在哪个时间窗对客户点进行服务,就需要在该时间窗内完成服务并离开该点。
2 模型求解
为验证所构建模型的可用性,利用Matlab软件生成一系列随机算例,并结合物流配送企业实践,选定混合整数规划模型所涉及主要参数的具体取值。
2.1 条件设定及主要参数选取
网络节点坐标采用随机生成的方式,以1 km为单位,建立笛卡尔坐标系。首先指定配送中心的位置,假定配送中心分布在边长为90 km的正方形区域内,其坐标为在该范围内生成的若干个点,且任意两点间的距离应大于15 km。接着在各配送中心的辐射范围(服务半径)内,生成相应的客户点坐标,且任意两个客户点之间的距离应大于300 m。鉴于客户点的多时间需求,设定客户点在一个工作日内的所有时间窗均位于区间[5,18],针对每个客户点都在该区间内随机生成多个没有交集的时间窗,且任意时间窗的长度至少大于配送卡车在该点的服务时间。
算例中主要参数取值如表2所示。
2.2 求解与结果分析
运用Cplex软件对不同规模的随机算例进行精确求解,计算结果如表3所示。
以算例7为例,网络中包含3个配送中心(D1,D2,D3),9个客户点,设定配送中心开放成本分别为0、50、100元/d。当pm=0元/d时,即不考虑配送中心开放成本,精确求解结果中的选址与车辆路径方案如表4所示,选择开放2个配送中心,目标函数值为315.56元;当pm=50元/d时,求解结果中的选址与车辆路径方案不变,目标函数值为415.56,新增成本即为配送中心成本;当pm=100元/d时,求解方案如表5所示,此时仅选择开放1个配送中心,相应配送路径方案也发生变化,目标函数值为466.54元。由此可以看出,当参数取值不同时,所得选址-路径方案与目标函数值也有所差别。

表2 主要参数取值

表3 算例的精确算法求解结果
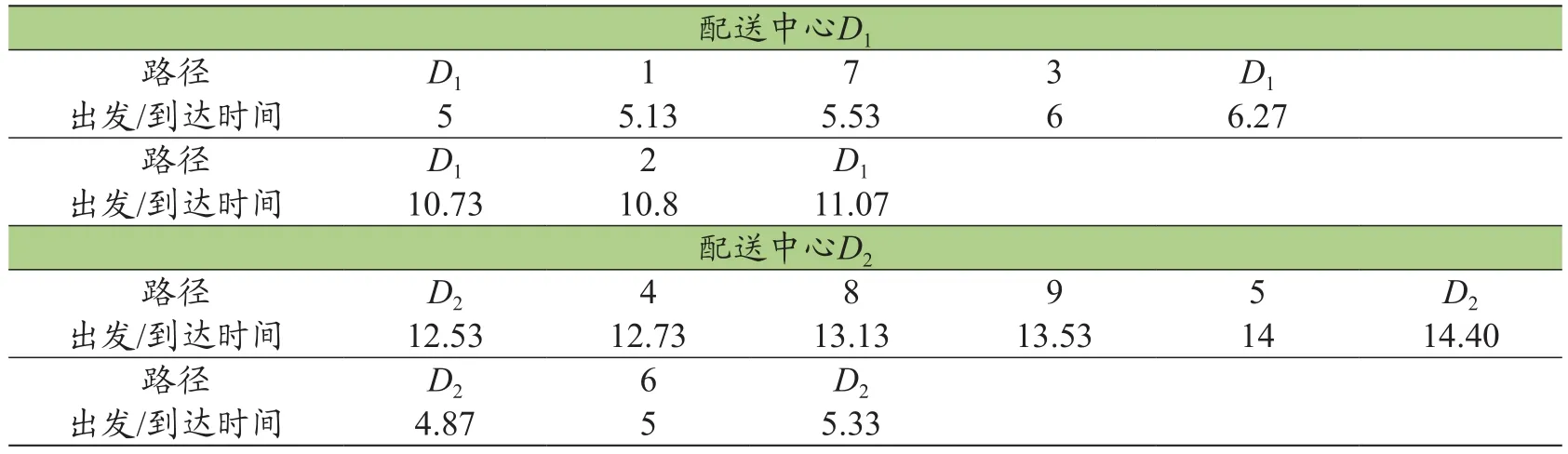
表4 算例7精确解的选址-路径方案(pm=0元/d)

表5 算例7精确解的选址-路径方案(pm=100元/d)
求解结果表明,随着算例规模增大,目标函数值呈上升趋势,且当参数取值(m、n、pm)相同时,不同算例的运算结果也相对平稳。针对同一算例,配送中心的开放成本若取不同的值,将对结果产生较大影响,若不考虑配送中心开放成本,在选址方案中会选择开放更多的配送中心,尽可能减少运输过程中的配送成本;而当配送中心的开放成本逐渐增大时,将会减少配送中心的开放数量,使得总成本最小。
3 结 语
面向带多时间窗的多配送中心选址-路径规划问题,构建混合整数规划模型,利用Cplex软件对随机生成的算例进行精确求解,通过对选址方案与车辆路径的优化实证,验证所建模型的有效性。在实践中,应合理权衡选址中心开放成本与运输成本之间的关系,做出最优决策。本研究丰富了选址-路径问题的建模手段,算例运算试验可为决策者提供参考。
