路侧式公交专用道对信号交叉口通行能力影响研究

(湖南省交通规划勘察设计院有限公司, 湖南 长沙 410200)

0 引言

实施交通需求管理政策，推动“公交优先”，引导人们选择高承载率的公共交通工具，是目前所倡导的热点政策之一。公交专用道是从空间的角度给予公交车辆不同程度的“路权优先”，实现公交服务水平的提高。公交专用道分为中央式公交专用道和路侧式公交专用道2种形式。由于路侧式公交专用道实施方便易行，且利于减少公交车辆出入干扰，方便乘客候车、登乘，城市道路网多选择路侧式公交专用道形式。

本文根据路侧式公交专用道设置特点，总结了影响信号交叉口通行能力的因素，通过设计VISSIM仿真方案定量分析了各影响因素对信号交叉口通行能力的影响程度，得到设置路侧式公交专用道的信号交叉口通行能力的折减系数模型，从而为公交专用道在城市道路中的布置提供理论支持。

1 信号交叉口通行能力影响因素分析

1.1 理论模型

我国《城市道路设计规范》定义交叉口进口道的通行能力等于各车道通行能力之和。其中，一条直行车道的通行能力CS的计算公式为：

(1)

式中：Tc为信号周期；t绿为直行绿灯时间；t损为一个周期内绿灯损失时间，一般取2.3 s；ti为前、后2辆车通过停车线的平均间隔时间，一般取2.5 s；φ为折减系数，一般取为0.9。

本文以上述模型作为通行能力基础模型，并进行了如下的假设：

1) 对设有左转专用信号灯的交叉口而言，左转车道的计算模型与直行车道的计算模型是相同的，且其中的t损、ti的取值相等。

2) 右转车道的计算模型为C右=β右CS，其中β右为右转车辆与直行车辆的比值；直右车道的通行能力计算模型为C右=CS。

1.2 影响因素分析

本文根据路侧式公交专用道设置特点，提出了绿信比、分流比、公交专用道截止线距停车线距离、左转公交车辆数等4个通行能力影响因素。

1) 绿信比。

在信号交叉口通行能力理论模型中，信号周期和有效绿灯时间都对通行能力有影响，而绿信比能综合体现这两者对通行能力的影响,交叉口某方向进口道对应的总绿信比决定了该方向车流的有效通过时间长短。

2) 分流比。

交叉口的交通分流比反映了不同流向的车辆交通量分布，本文研究的分流比是指交叉口直行流量与左转流量之间的比率。当直行流向的交通量较大时，左转车辆可利用的直行交通可插间隙变小，从而影响左转车道通行能力；当左转流向的交通量较大时，将会有较多的换道交织行为，从而影响直行车道的通行能力。

3) 公交专用道截止线距停车线距离。

对于设有公交专用道的道路，在交叉口无公交专用进口道的情况下，公交车辆在交叉口处需要离开专用道并入普通机动车道。如果专用道截止线距停车线的距离比交叉口的排队长度短，则在短时间内不能为从专用道并入普通机动车道的公交车辆提供合适的车流间隙，导致交叉口交织严重，从而降低了通行能力。

4) 左转公交车辆数。

对于路侧式公交专用道而言，从公交专用道驶出的左转公交需要从最外侧车道换道进入最内侧的左转专用道，它对交叉口的交织情况也会有影响,见图1。

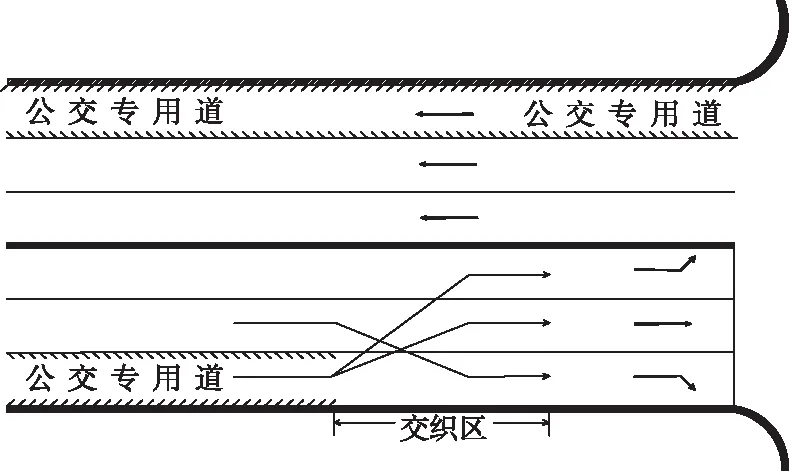
图1 设置公交专用道的交叉口示意图

2 仿真案例分析

从理论模型可以看出，绿信比与通行能力呈线性关系，折减系数φ的值一般取为0.9，随着路侧式公交专用道的设置，该折减系数不能反映公交专用道对信号交叉口通行能力的影响。随着分流比、专用道截止处距停车线距离和左转公交车辆数取值的不同，交叉口处的交织严重程度也是不同的，折减系数φ也随之变化。本文利用VISSIM软件定量分析分流比、专用道截止线距停车线距离和左转公交车辆数与信号交叉口通行能力、折减系数的关系，提出通行能力修正模型。

2.1 仿真方案设计

本文利用VISSIM软件搭建了路段仿真平台。仿真平台为进、出口道双向6车道的十字交叉口，车道宽度为3.5 m，最外侧的机动车道为公交专用车道。

针对影响因素设计了全组合仿真方案，表1为各影响因素在仿真方案中的不同取值。通过利用VISSIM平台改变影响因素的取值，可以模拟多种不同交通情况，然后通过不断加载路网入口流量，获得在多种交通情况下的通行能力值。

表1 影响因素在仿真方案中的取值分流比专用道截止线距停车线距离/m左转公交数/辆1.5,2.25,3,3.75,4.5,5.25,6,6.75,7.5,8.25,9,9.75,10.5125,150,175,200,225,2500,10,20,30,40,50,60,70

2.2 仿真分析

1) 分流比。

本文利用SPSS对分流比与通行能力、折减系数的函数关系进行拟合。通过多组数据分析，发现分流比与通行能力拟合成Inverse型曲线效果最优，分流比与折减系数拟合成Power型曲线效果最优，分别见图2、图3。

从图2、图3可以看出，分流比与折减系数的变化趋势和分流比与通行能力的变化趋势不一样。这是由于分流比对理论模型中的直行绿灯时间有影响，依据信号配时的基本原理，绿灯时间与该相位的流量比成正比，因此在理论模型中，直行绿灯时间与分流比之间的关系为：

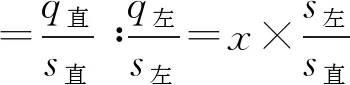
(2)

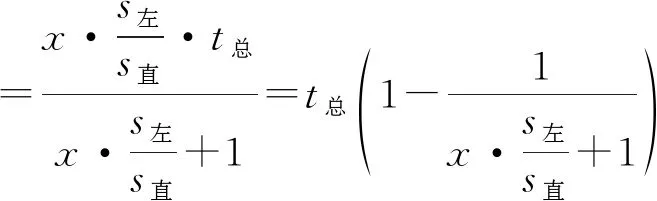
(3)

式中：t直为直行绿灯时间；t左为左转绿灯时间；s直为直行车道数；s左为左转车道数；q直为直行流量；q左为左转流量；x为分流比；t总为总绿灯时间。

因此在理论模型中，分流比与通行能力拟合是Inverse型函数关系。将理论模型与折减系数相乘后，由于折减系数中x的幂次很小，可以认为分流比与通行能力仍然符合Inverse型函数关系。因此，分流比与折减系数的Power型函数关系是合理的。

图2 分流比与通行能力的关系

图3 分流比与折减系数的关系

2) 专用道截止线距停车线距离。

本文利用SPSS软件对公交专用道截止线距停车线距离与通行能力、折减系数的函数关系进行拟合。通过对多组数据的分析，截止距离与通行能力也拟合成S型曲线效果最优，截止距离与折减系数拟合成S型曲线效果最优，分别见图4、图5。

从图中可以看出，当截止线与停车线间的距离从150 m增加到200 m时，折减系数有较大的提高；当截止线与停车线间的距离达到200 m以上时，折减系数的增长趋势趋于平缓。

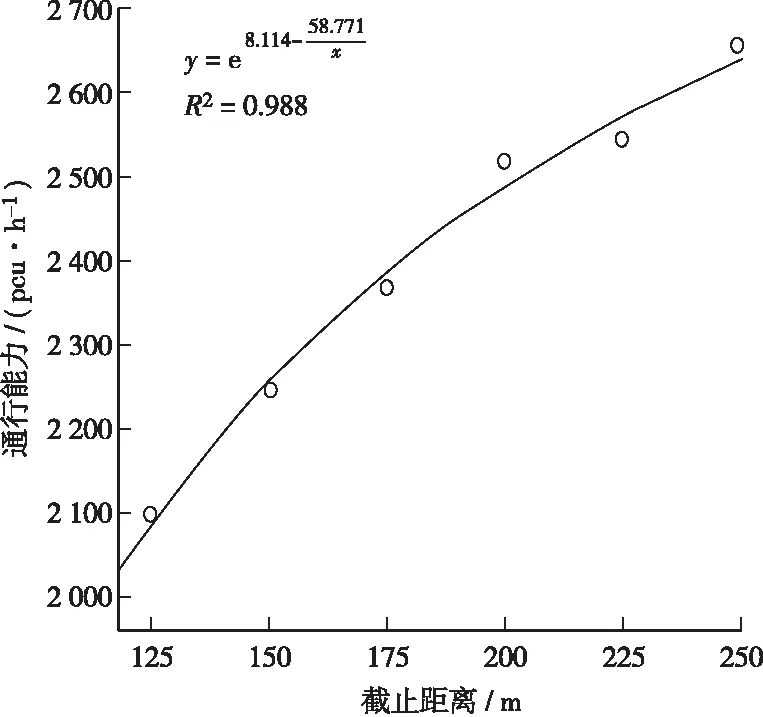
图4 专用道截止线距停车线距离与通行能力的关系

图5 专用道截止线距停车线距离与折减系数的关系

3) 左转公交车辆数。

本文利用SPSS软件对左转公交车辆数与通行能力、折减系数的函数关系进行拟合。通过对多组数据的分析，左转公交车辆数与通行能力拟合成二次函数曲线效果最优，左转公交车辆数与折减系数也拟合成二次函数曲线的效果最优，分别见图6、图7。

图6 左转公交车辆数与通行能力的关系

从图中可以看出，随着左转公交车辆数的增加，折减系数有所减少。当左转公交车辆数从0变化到40时，折减系数变化较为平缓，当左转公交车辆数继续增大时，折减系数有了较明显的减少。由此可知，左转公交数量越多，其对通行能力的影

图7 左转公交车辆数与折减系数的关系

响越大。

2.3 通行能力模型修正标定

通过分别分析3个影响因素与折减系数的函数关系，最终确定折减系数的函数表达式为：

(4)

利用VISSIM全组合仿真方案，获得在多种交通情况下的折减系数，然后利用SPSS对多组数据进行多元回归拟合，从而确定出上述公式中的各参数取值。因此，主干道设置公交专用道的通行能力折减系数模型为：

0.000 2x3+0.997)

(5)

2.4 模型的验证

为了对模型进行有效性分析，本文采用了4个误差评价指标，分别为平均相对误差(MeRE)、最大相对误差(MaRE)、平均绝对误差(MeAE)和最大绝对误差(MaAE)。

分别计算改进前模型、改进后模型的以上4个指标，各误差评价指标的具体值如表2所示。从表2可以看出，改进后模型的计算结果与仿真结果的误差更小。

表2 模型误差指标表类别MeRE/%MaRE/%MeAEMaAE模型改进前9.621.6194.8484.7模型改进后4.613.897.3302.1

3 结论

本文基于信号交叉口通行能力理论计算模型，总结分析了路侧式公交专用道对信号交叉口通行能力的影响因素，根据大量仿真样本得到了基于分流比、公交专用道截止线距停车线距离、左转公交车辆数等影响因素的折减系数修正模型,为城市道路设置路侧式公交专用道提供理论支持，对公交专用道在主干道的建设具有现实意义。