无尾扑翼无人机动力学建模及仿真
2020-06-29陈登峰1耿建勤
陈登峰1,耿建勤,张 温,刘 国
(1.西安建筑科技大学 建筑设备科学与工程学院,西安 710055;2.西安建筑科技大学 信息与控制工程学院,西安 710055)
0 引言
扑翼无人机常用于战场侦察、飞行巡逻、边境渗透、无线中继、仿生研究等领域,国内外仿生扑翼型无人机技术在近年取得重大进展,微型扑翼无人机将升力、转向、悬停、推进集中在一起,在仿生学以及军事领域有突出的应用前景[2,7-8]。例如西北工业大学设计的“信鸽”仿鸟扑翼无人机被誉为突防敌方雷达监测的“间谍鸟”[9],微型扑翼无人机由于其巨大的应用潜力而引起国内外的热门研究,其中对无人机飞行控制及建模研究尤为重要[6]。刘岚[10]等采用数值模拟的方法研究了扑翼飞行的气动力学问题;董维中[11]等提出了一种基于X型的微型扑翼飞行器;付鹏[12]提出了一种扑翼专用的扑翼机构,分析了扑动频率、扑动幅度与推力的关系;A.Roshanbin[13]等基于双扑翼微型飞行器进行仿生设计,介绍了基本运动方法;W.L.Chan[14]用仿真实验得到重心位置变化会产生俯仰力矩。综上针对无尾扑翼无人机的建模研究较少以及扑翼无人机纵向飞行动力学建模过程的复杂问题,文章提出一种纵向刚体力学模型,该模型是建立在xOz面的纵向姿态控制,并进行在不同的俯仰角度下验证模型的有效性。TFWR升力由两对薄膜机翼扑动产生,机翼的翼根与中心轴组成二面角,调节二面角实现无人机的多维运动[15]。
1 模型及飞行方法
无尾扑翼无人机的计算机辅助设计如图1所示,机翼主要参数如表1所示,机翼采用X的设计方式,在飞行时左右机翼产生频率和幅值相同的扑动,有效减少机翼引起的振动,扑动时机翼所受大小相等方向相反的阻力,使机身所受合力最小。无人机没有尾翼,飞行的稳定和姿态调整是依靠机翼的扑动和扑动角度实现的。整体由两对电机独立控制的两对机翼组成,扑动频率独立调制,每对机翼扑动方向相反,偏航控制的翼根方向相反。如图1翼长为0.34 m,机体建模为a×b×c的长方体模型,其质量均匀分布,质心位于几何中心,机翼推力中心为COP,COP与质心在x轴的距离为lx,COP与质心在z轴的距离为lz为常数。
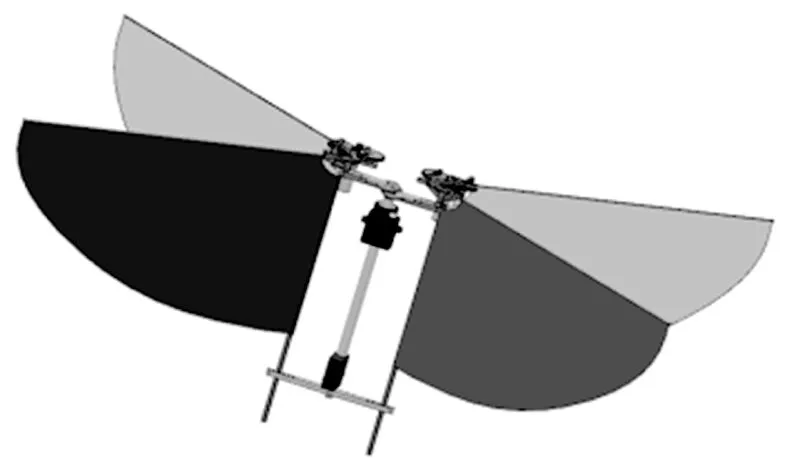
图1 计算机辅助设计图
机翼由前缘和翼根的两根碳纤维杆和薄膜构成,由于机翼的翼面采用薄膜构成,在摆动时翼襟摆动的角度大于前缘杆的摆动角度,如图2所示。TFWR有4个机翼用于推进和控制,其摆动的方向相反,因此减少了由机翼阻力对机体的影响。无人机采用无尾翼形式,通过调整其4个机翼的运动实现主动稳定[16],机翼参数如表1所示。
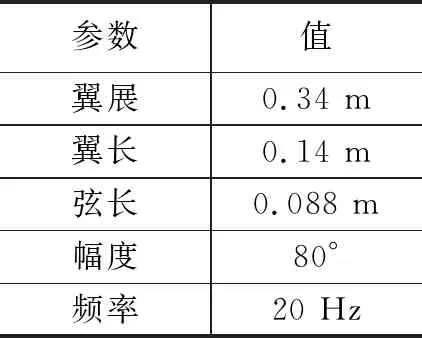
表1 无人机参数表

图2 无人机坐标系
建立无人机坐标系xyz,坐标原点O与质心重合,其中y轴为原点指向翼根方向,z轴为原点指向前缘方向,x轴方向与yOz面垂直,xOz面内的姿态角为俯仰角、xOy面内的姿态角为偏航角、xOy面内的姿态角为滚转角,如图2所示。研究发现,仿生扑翼无人机通过机翼的扑动和调整扑动的夹角完成飞行姿态调整,其过程描述如下:通过独立调整左右机翼的扑动频率f,实现无人机的滚转运动;通过调整翼根的方向,实现偏航运动;通过改变扑动的二面夹角,实现俯仰运动。其中俯仰力矩是依靠机翼的二面夹角产生,左右机翼振幅的变化是相同的,在翼长R/2处为机翼的推力中心COP,通过调整二面夹角是的推力中心与质心偏移产生lx,得到俯仰力矩。
2 动力学模型
2.1 机翼动力学模型
为了准确地描述无人机机翼的动力学特性,1996年C.P.Ellington对飞蛾等进行风洞测试[17],发现在机翼扑动时会由于延时失速从而产生升力,机翼扑动过程中迎角为正,产生两次前缘涡为机翼提供升力。采用叶素法[18]和准稳态模型[17]对机翼和机体建模,假设机体瞬时受力仅由机翼运动决定,同一翼上产生的力以相同的瞬时速度和迎角稳定运动,作用在机翼平面上的气动力是每一个小展片上的气动力之和,根据瞬时受力预测出任意运动模式下的机翼动力,通过计算瞬时气动力进行翼面运动分析。为了计算气动力,假设有一翼面位移的速度V及其迎角α如图3,将翼面在均匀介质中运动所受合力分解成纵向垂直分量和横向水平分量。
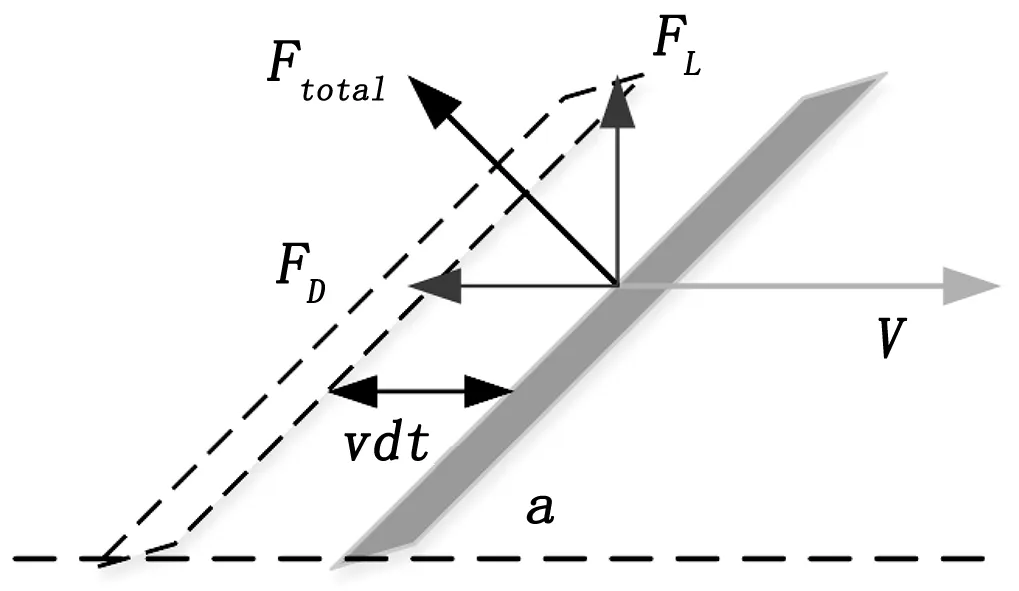
图3 翼面运动受力
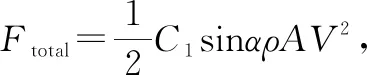
就课程具体内涵而言,“岭南艺术”特色课程核心系列的音乐专业课主要是让学生在岭南艺术素材的基础上进行演唱、演奏、表演和创作;美术专业课则让学生以岭南艺术素材进行素描静物、素描头像、人物速写、风景速写、创意素描和创意色彩等创作。
基于以上对翼面运动的分析计算,进一步对无人机机翼运动受力分析。TFWR包含两对运动对称的机翼,机翼由前缘、翼根和翼面组成,每只机翼摆动的幅度和频率相同,其摆动是根据电机带动运动机构进一步驱动前缘运动,使得整个翼面扑动。TFWR采用纵向飞行的运动模式,静止时机翼的翼面与水平面垂直,要使在翼面摆动时与水平面产生的迎角为锐角,则会产生图3的翼面效果产生升力分量FL,则设计的翼根与前缘在静止时应大于90°如图4(a)所示,机翼运动时所受阻力与翼面垂直,分解为运动阻力FD和运动升力FL,其中机翼的气动力组成如图4(b)所示。
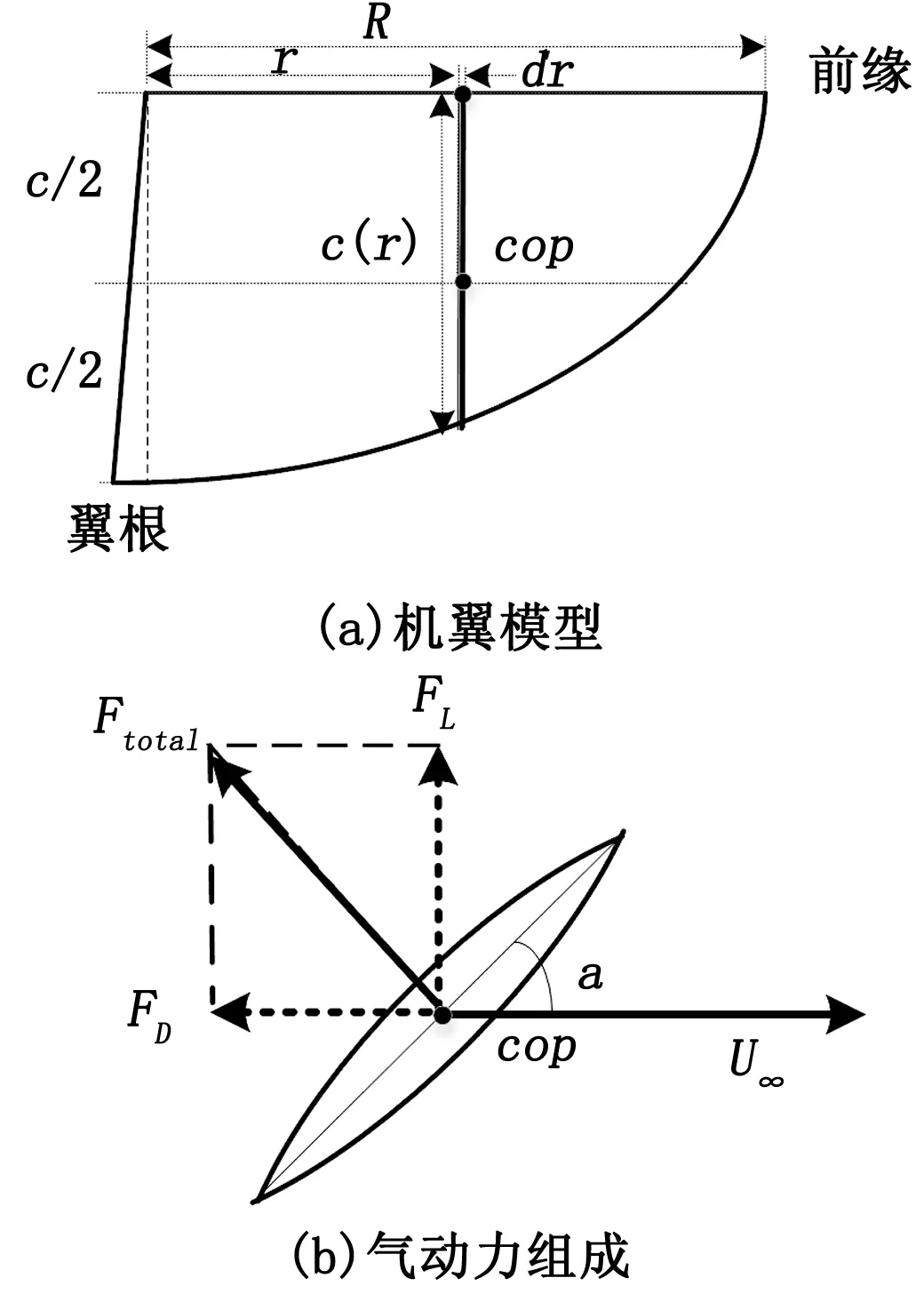
图4 气动力组成和机翼模型
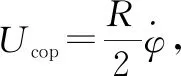
(1)
即:
FL=2CLρAUcop2
(2)
即:
FL=2CLρAUcop2=2CLρA(πRf)2
(3)
同理得:
FD=2CDρAUcop2=2CDρA(πRf)2
(4)
式中,CL、CD根据经验公式CL(α)=0.225+1.58sin(2.13α-1.72),CD(α)=1.92-1.55cos(2.04α-9.82)[19],其中U表示运动机翼推力中心速度,φ表示运动振幅,升力的计算是根据叶素法在机翼的受力在翼展半径上的积分得到,由式(4)知机翼的升力与运动速度的平方成正比,且随着扑动频率增加而增加,机翼的阻力有相同的规律。
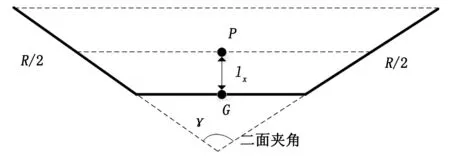
图5 二面角示意图
无人机的左右两侧各驱动一对机翼,利用机翼扑动以提供升力,相反的机翼对机体的扭力相互抵消,减少机体振荡和应力。无人机在运动时由左右两对机翼在固定扑动频率下产生的合力进行俯仰姿态调整,由于在运行时机翼的摆动频率设定为20 Hz,假设在周期内按照平均升力计算,则左右机翼的推力在推力中心COP处的合力简化为FT=4c2f2,c2为机翼的升力系数。在固定频率模式下每个机翼产生的升力为定值,二面体机构通过调整二面角γ即改变COP与质心距离lx如图5所示。当一个机翼在周期性运动时,除扑动频率外其他参数保持不变,产生的推力只依赖于扑动频率,且不受机体空气速度的影响,利用机翼受力计算得到机翼的扑动频率与其产生升力的关系如图6所示,图中横轴表示机翼的扑动频率,纵轴表示单机翼和双机翼的瞬时升力。
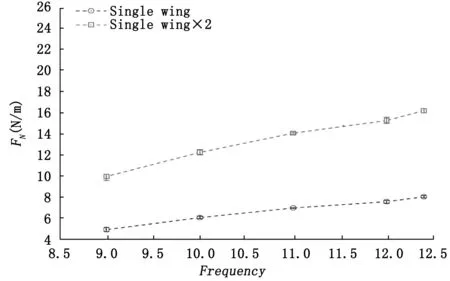
图6 扑动频率与推力关系
2.2 机体纵向动力学模型
针对无尾扑翼无人机机体姿态动力学建模,文章提出一种无尾扑翼机器人纵向动力学模型,该模型基于刚体动力学分析,用于无人机从悬停到前进,利用机翼产生的升力模型及调节二面角γ进行俯仰控制,建立机体力学模型,并对模型进行仿真验证,整体模型结构如图7所示。
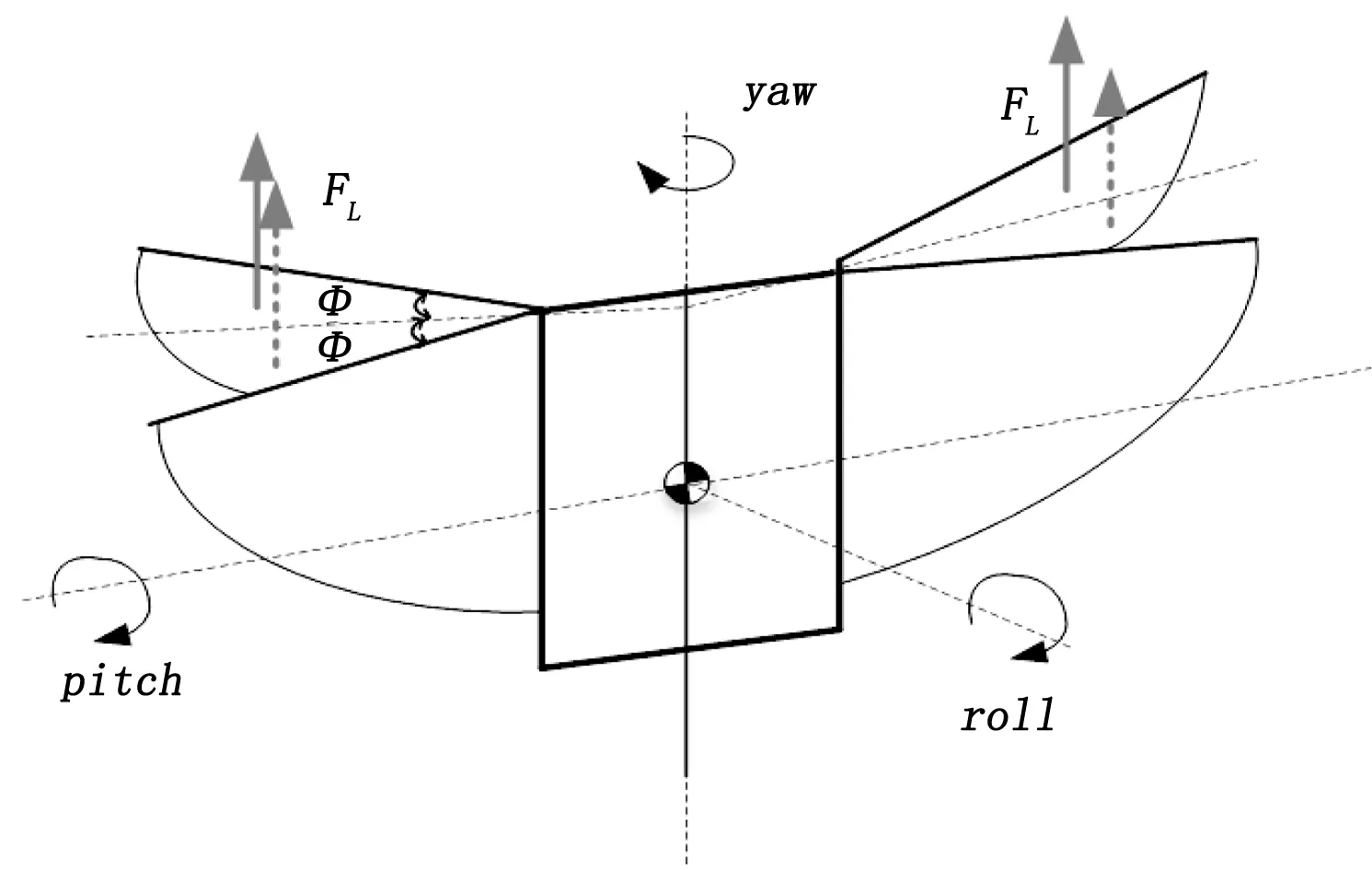
图7 模型纵向运动示意图
假设无人机是刚性的,机翼和扑动机构没有质量,利用准稳态假设机翼在上扑和下扑过程中以恒定的速度和迎角拍打, 则质心是无人机内的一个固定位置,如图7所示,根据标准刚体运动方程,无人机的纵向刚体力学模型如图8所示。所有气动效应均源于扑翼,且忽略了机体的阻力。这两对机翼由推力F和阻力D表示。在模型中,俯仰转矩是由相对于质心和推力中心的纵向位置lx产生。
在xOz平面建立机体纵向动力学模型:
(5)
(6)
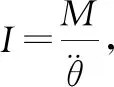

(7)
得到纵向动力学方程:
(8)
(9)
(10)
式中,m为质量,I为沿侧身轴的惯性矩,g为重力加速度,u为纵向速度,v为法向速度,θ为机体俯仰角度,FX纵向机体受力,FZ机体法向受力,M为俯仰力矩,D为阻力。纵向动力学的模型是根据在x轴和z轴以及质心处扭矩动力学方程建立,如图8所示。
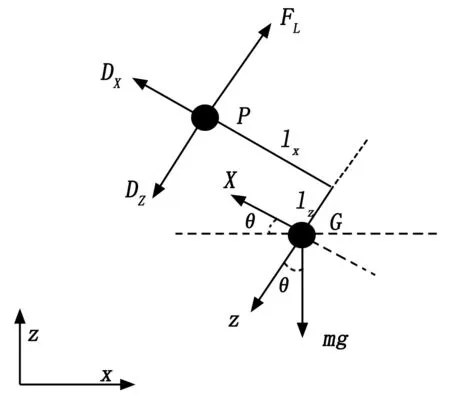
图8 纵向刚体力学模型
由于模型适用于任何方向的飞行,所以机翼阻力有纵向和法向分量:
DX=-KXfv′
(11)
DZ=-KZfu′
(12)
其中:KX和KZ为在x轴和z轴的力系数,u′和v′为COP的纵向和法向分量。阻力由扑动频率和推力中心运动速度确定。速度分量以表示为:
(13)
(14)
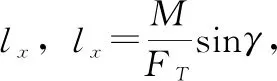
FZ=FT
(15)
FX=mgcosθ
(16)
M=DXlx+DZlz
(17)
得到完整的纵向飞行动力学方程:
(18)
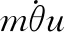
(19)
(20)
该模型有两个输入量:二面夹角γ和扑动频率f,其他参数:质量m、转动惯量I、阻力系数KX和KZ、合力中心与质心的纵向位置lz均为测量的值。为了验证模型的有效性,采用表2所示的参数设置。
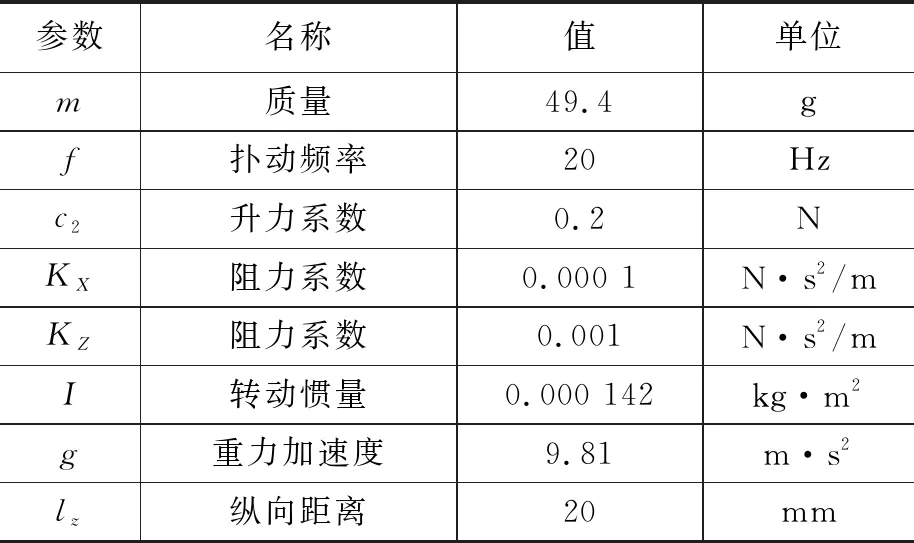
表2 参数设置表
3 仿真及结果分析
在模型验证时,采用固定扑动频率20 Hz,参数设置按照表2所示。无尾扑翼无人机系统在Simulink中实现的整体模型结构如图9所示。仿真模型包含TFWR纵向动力学模型和控制系统模型,控制系统采用PID控制模式,仿真模型的输入值为俯仰设置角度,输出值有纵向速度、法向速度、俯仰角度、俯仰角速度、俯仰角加速度以及切向距离。
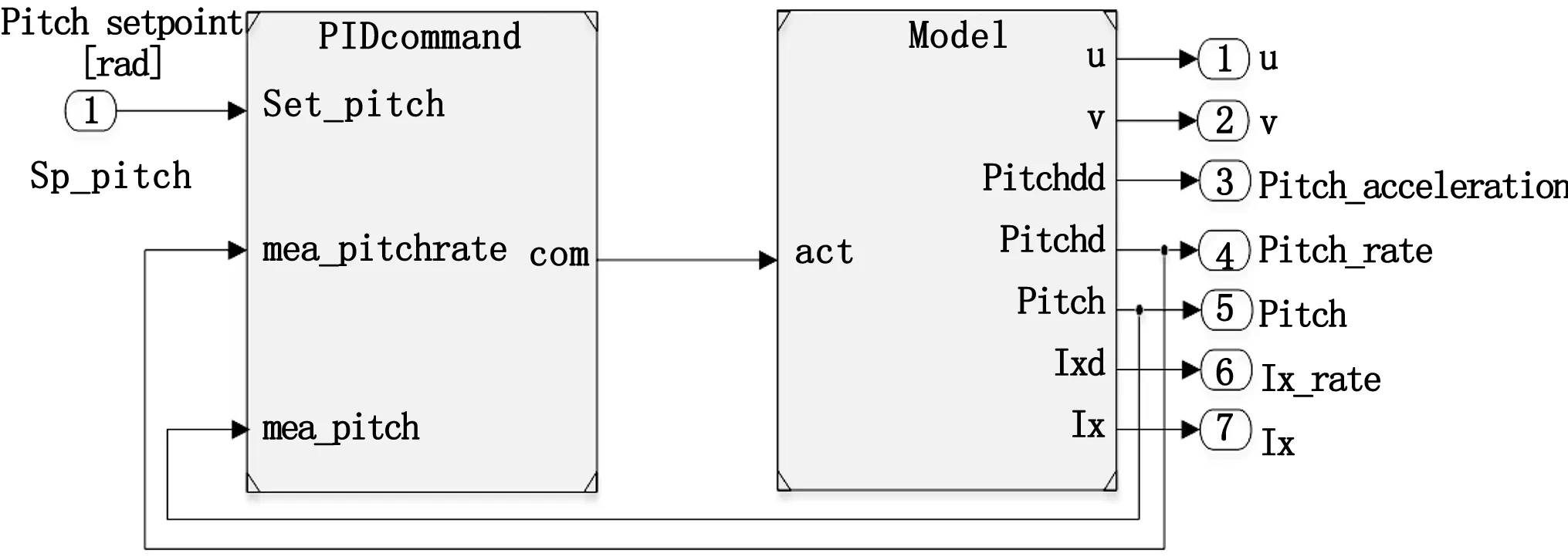
图9 无尾扑翼无人机控制结构仿真模型
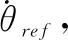
TFWR以悬停稳定为出发点,利用机翼扑动频率与其升力的关系,得到机体姿态在设定角度下的响应情况。纵向动力学模型通过在Simulink中进行实验,设定俯仰角度为±15°、±30°,TFWR从平衡状态到响应±15°、±30°俯仰角的情况如图10、图11所示。
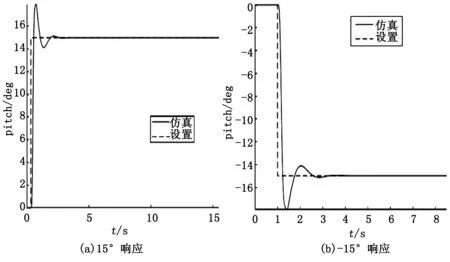
图10 俯仰无人机响应
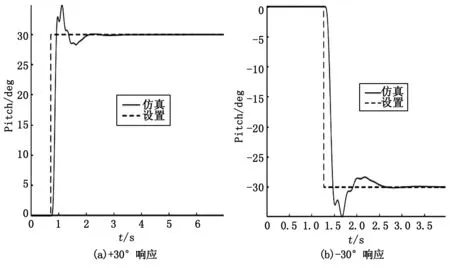
图11 俯仰无人机响应
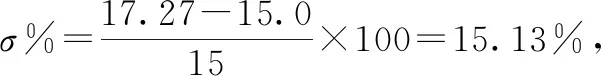
4 结束语
针对传统仿生扑翼无人机的飞行建模较为复杂、计算难度较大的问题,文章基于叶素法、准稳态假设模型以及刚体动力学建模方法,提出一种基于无尾扑翼的机翼的动力学和机体纵向动力学模型,对机体纵向飞行建模分析,得到机体的三个运动学关系:机体的纵向受力关系、法向受力关系、质心扭力关系。为了验证模型有效性,在Matlab/Simulink进行了TFWR的闭环仿真实验,设置从平衡位置到15°、30°俯仰角,实验表明,系统的超调量分别为15.13%和16.23%,调节时间分别为0.5 s和1 s,基本以快速响应且稳态误差较小,可以达到控制要求,符合实验预期。
