不同支配关系的多目标算法的柔性作业调度

李晓辉，刁林倩，张 秀2，赵 毅，李 杰

(1.长安大学 电子与控制工程学院, 西安 710064; 2.陕西汽车集团有限责任公司，西安 710119)

0 引言

随着大批量连续生产时代正逐渐被适应市场动态变化的多品种、小批量离散生产所代替，一个制造企业的生存能力和竞争能力在很大程度上取决于它是否能在较短的生产周期内，生产出较低成本、较高质量的多个产品品种的能力。柔性制造系统(FMS)是高度自动化的生产系统，能够生产各种各样的作业类型。许多FMS采用自动制导车辆系统(AGVS)，这是各种先进的材料处理技术之一。由于缩短交货期一直是工业界的一个重要目标，因此FMS调度受到了广泛的关注。在灵活作业车间调度问题(FJSP)[1]中，每个作业都可以在任何可用的机器上执行。J.Blazewicz等人[2]指出，FMS中最困难的操作问题之一是对所有所需资源的生产顺序和时间分配进行适当的协调，即开发考虑工作、机器和车辆的高效FMS调度计划。开发高效的FMS调度仍然是一个重要而活跃的研究领域。近年来，对FJSP的扩展进行了研究，提出了不同的精确和近似方法来解决这一问题，以编制接近实际的调度。关于FJSP建模的最早研究可以在P.Brucker和R.Schlie[3]中找到，提出了一种考虑两种工作的多项式算法来解决这类问题。近年来，一些问题也采用了精确的方法。例如，M.Mousakhani[4]使用混合整数线性规划(MILP)方法解决了设置时间依赖于序列的FJSP问题。

典型的半导体自动化制造单元，如：M.Dawande等人[5]，C.R.Pan等人[6]，如图1所示，装备了一个搬运机器人，可以在工作站之间精确地运送作业。当作业在工作站上完成当前处理阶段时，机器人执行加载的移动，包括3个步骤:从工作站上卸载作业，将其传输到下一个工作站上并将其加载。连续地，机器人要么在工作站上等待同一作业的下一个移动，要么在没有任何作业的情况下执行空洞移动，以移动到另一个工作站上执行下一个作业的移动。在这种情况下，作业移动及其持续时间在调度过程中不能被忽略。自动化作业运输机器人在化工、电镀处理和金属切削行业也很常见如：车阿大等[7]，晏鹏宇等[8]，Gultekin等[9]。这种以机器人为中心的制造系统称为机器人单元。

图1 一个典型的带有材料处理机器人的机器人单元

实际应用问题中往往需要同时优化几个目标，在多目标问题求解中，由于各目标之间是相互矛盾的，所以不能找到一个优化解使得所有优化目标达到最优，因此我们的目的是找到一个非支配解的集合代替仅有的一个最优解。近10年来，国内外许多研究者相继提出大量的优化算法，如NSGA-II[10], SPEA-II[11](strength pareto evolutionary algorithm)等在解决多目标优化问题上取得了很好的效果。但是随着目标维数的增加，基Pareto支配关系的多目标进化算法收敛性能下降，在求解过程中出现了种群早熟，收敛停滞，非支配解的比率过大的现象。虽然通过扩大种群规模，可以一定程度上缓解非支配解比例过大的问题，但却增加了求解过程的计算难度。

对于多目标优化问题，研究人员往往从三方面对算法进行改善[12]：1)基于Pareto支配关系，进行目标降维;2)采用不同的支配方法，如：占优，Lorenz[13]支配，CDAS[14]支配，r[15]支配等;3)引进新的策略或机制。肖婧[16]等人提出基于全局排序的高维多目标优化研究，巩敦卫[17]等人提出基于目标分解的高维多目标并行进化优化方法，陈小红[18]等人提出基于稀疏特征选择的目标降维方法，与此同时将不同的支配方法和传统优化算法结合去求解高维多目标优化问题也是研究的热点，如Atefeh Moghaddam[19]将不同的支配方式和算法相结合求解调度问题，通过大量案例比较算法的优越性。

多目标优化问题和调度问题现在都是我们研究的热点，本文的目的就是通过不同的方法求得优化问题的最优解，应用不同的支配方式去求解带有机器人搬运的柔性作业车间调度问题，以传统的NSGA-II为框架，分别基于Lorenz支配关系和CDAS支配关系对问题进行求解，并将所得的解通过[13]距离准则和C[20]准则进行比较分析。

1 问题描述

1.1 研究问题

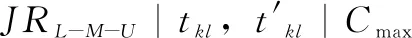
参数定义如下：

J为工件集合，J={J1,…,Jn};

M为工作站集合，M={M0,M1,M2,...,Mm},M0为装/卸载站;

I为根据工件序列，工件操作集合I={1,2,…,|I|};

lij为工作站i到工作站j之间的带载移动时间，(i,j)∈M2;

vij为工作站i到工作站j之间的空载移动时间，(i,j)∈M2;

μi为操作i(i∈I)对应的加工站;

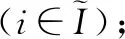
H为一个很大的正整数;

ti为操作i的完成时间，i∈I;

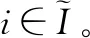
Cj为是工件j的完工时间:

(i,j)∈I2并且μi=μi,i≠j;

(r,s)∈T2并且r≠s;

(r,s)∈T2并且r≠s

本文研究问题数学模型引用Caumond[22]论文中的数学模型，假设条件为：

1)同一工件根据加工顺序执行不同工序；

2)同一工作站在同一时刻只能执行一道加工操作；

3)同一时刻搬运机器人执行一个搬运操作；

4)工件搬运时间约束，工件前道工序加工完成后才能搬运；

5)不考虑机器和机器人故障；

6)不考虑机器人和加工站之间的装载和卸载时间；

7)无优先处理约束，缓冲管理规则为FIFO(First In First Out)。

目标函数：

(1)

minimizeα∑Ej+β∑Tj

(2)

其中:α和β分别代表总提前量与总延迟量的权重。Ej和Tj代表工件j的提前量和延迟量。

Ej=max(0,aj-Cj)

(3)

Tj=max(0,Cj-bj)

(4)

其中:aj和bj表示工件j的最早到期日和最晚到期日。

1.2 解的支配关系

本节介绍了三种支配关系：Pareto支配关系、Lorenz支配关系和CDAS支配关系。下面以一个最小化的多目标遗传优化问题为研究对象阐述这三种支配关系：

MinF(X)=(f1(X),f2(X),…,(fn(X)))T,x∈D

(5)

其中:X=(x1,x2,...xm)T是决策变量，fi(i=1,2,...n)是目标函数，D是可行区域。

1.2.1 Pareto支配

给定一个多目标优化问题，设X为多目标优化问题的可行解集，目标向量为F(x)=(f1(x),f2(x),...fm(x))，xl∈X,xk∈X,若:

∀i∈{1,2,…,m}fi(xi)≤fi(xk)

∃j∈{1,2,…,m}fi(xi)≤fj(xk)

(6)

则称xlPareto支配xk(记作xlxk)，Pareto支配关系如图2所示，区域①为解S的Pareto支配区域。

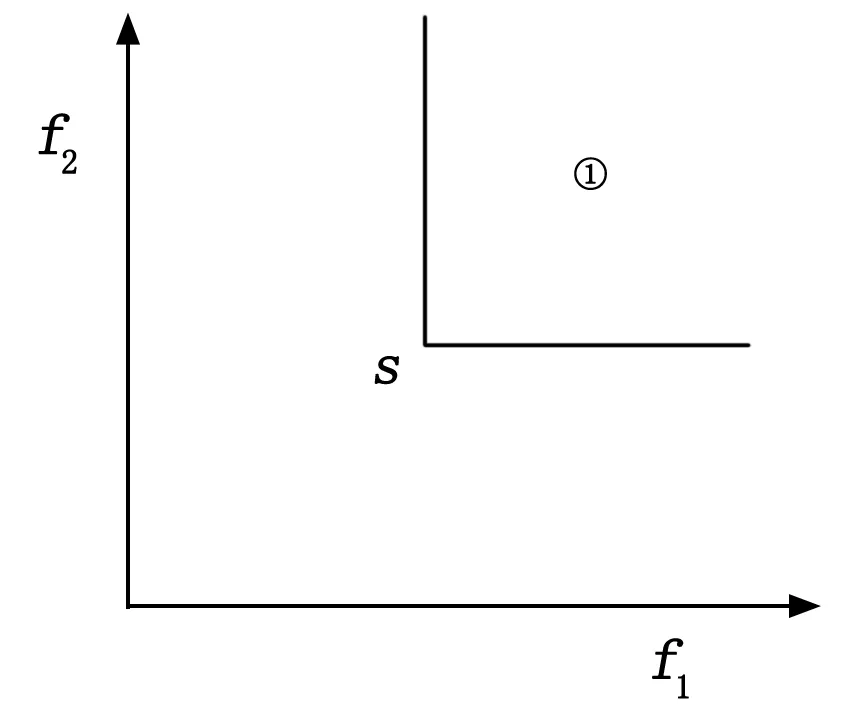
图2 Pareto支配关系

1.2.2 Lorenz支配

多目标启发式算法一般情况下都是基于Pareto支配关系找到一组非支配解集，但是Lorenz支配可以减少非支配平面的范围，提高算法的搜索能力。F.Dugardin[13]等人在其文章中提到Lorenz 支配能够提高解的质量，它更擅长于双目标优化问题解的比较。Lorenz 支配是1934年Hardy等人第一次提出,之后Kostreva 和Ogryczak将其应用到对于解决多目标优化问题中。

基于Lorenz支配关系，如果解X支配解Y,记作XLY。如果解X的Lorenz矢量基于Pareto支配关系支配解Y的Lorenz矢量，记为L(x)pL(Y)。其中X的Lorenz矢量为：

L(x)=(f(1)(x),f(1)(x)+f(2)(x),f(1)(x)+

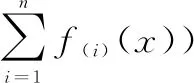
(7)

f(1)(x)=max(fi(x))∀i∈{1,2,...n}，f(2)(x)是fi(x)所有目标函数适应度值中从大到小排列第二的适应度值，依次类推。

根据Lorenz支配关系的定义，Lorenz支配将解的目标函数值收敛到未修改前其中一个目标函数值的附近。Lorenz支配关系如图3所示。对于解S，基于Pareto支配，S的支配领域为区域①。而基于Lorenz支配，S的支配领域为区域①,②,③。显然，Lorenz的支配区域要大于Pareto的支配区域,事实上Lorenz的非支配解是Pareto非支配解的子集。

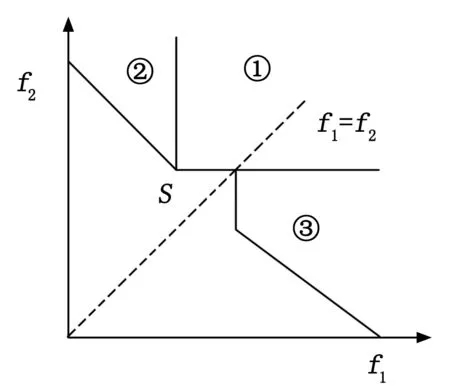
图3 Lorenz支配关系

1.2.3 CDAS支配

为了提高基于多目标优化进化算法的Pareto支配的选择压力，提出了一种新的支配关系CDAS。CDAS支配利用一个用户自定义参数S改变支配关系，是一种支配区域自适应变化的方法，它是利用支配关系来提高收敛压力。在多目标优化问题中，CDAS支配增强了解的搜索能力。经过试验发现，当S等于0.25时，寻求多目标优化问题最优解的效果最佳。

对于一个解x，根据公式(8)通过改变一个参数Si的值来修改它的每一个目标函数的适应度值，图4给出了解x经CDAS准则修改前后适应度函数值的变化情况。

(8)

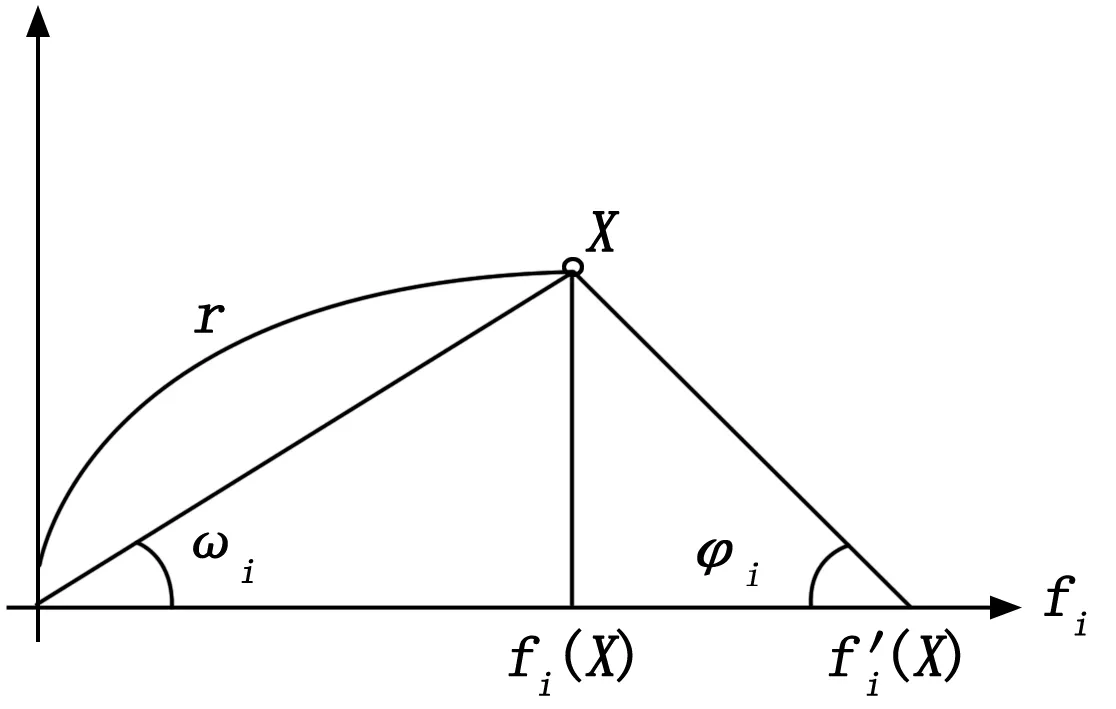
图4 解x修改前后适应度值

CDAS原本的方法是根据解x与原点两点间改变参数Si来改变解x的支配区域，然而，在我们研究的问题中有很多个解，且我们没有办法确定解的位置，想要找一个合适的参数Si也很困难，在本文中我们的目标值是最小化，我们对CDAS支配方法在算法应用进行改进，在这里首先做如下定义，如式(9)：

(9)

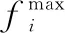
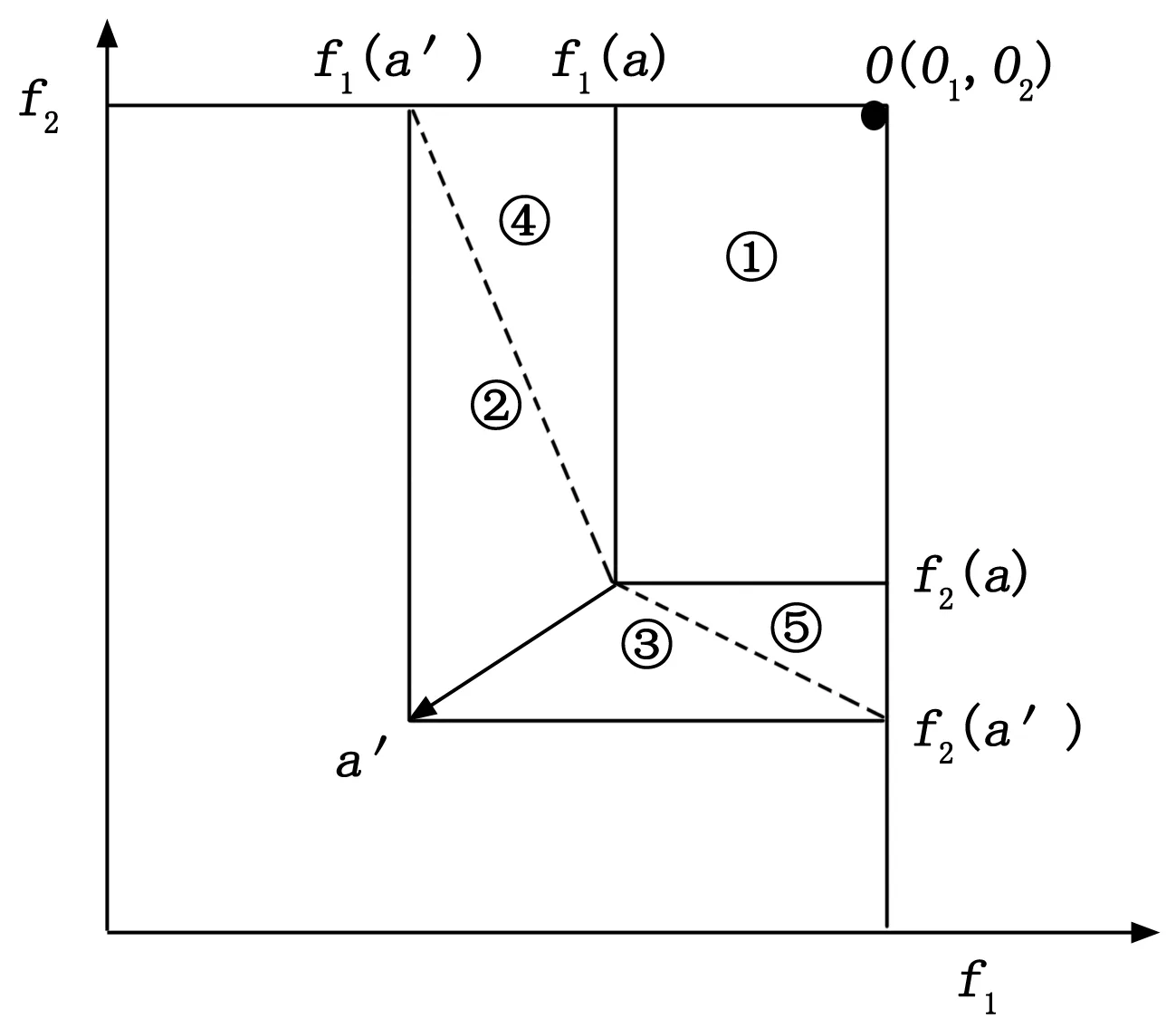
图5 CDAS的支配关系

2 算法

2.1 NSGA-II算法

NSGA-II非支配排序遗传算法，2000年由K.Deb,S.Agrawal,A.Pratap等人提出。该算法是基于Pareto支配的多目标进化算法，被广泛应用在多目标优化问题求解中，尤其是目标函数只有两到三个的优化问题。对于多目标优化问题，该算法得到的不是一个单独的解，而是一个非支配解的集合。

在NSGA-II算法中，首先随机生成一个初始种群f1(x)>f2(x)。在第t次迭代中子代f1(x)>f2(x)通过评估、选择、交叉、变异因子被生成。将f1(x)>f2(x)和f1(x)>f2(x)中所有个体排序到不同的前端(第一前端被认为包含所有的非支配解，为了找到下一个前端的解，之前已被排序的解不再考虑)。这个过程被重复，直到所有的解被排序，最好的解(拥有最优序值和最佳拥挤距离)将被选择作为下一次迭代中的父代种群f1(x)>f2(x)。当满足设定的停止标准时，整个迭代过程结束。

2.2 遗传算法因子

交叉变异：本文采用Q.K.Pan[23]等(2008)一文中提到的two-cut points PTL交叉法。该交叉法的优势在于：即使两个父代相同，经过PTL交叉也可以产生出不同的子代。在PTL交叉过程中，随机产生两个交叉位置，将父代1中随机产生的交叉位置上的基因作为子代1最左端和子代2最右端的基因，子代个体剩余部分的基因由父代2除去父代1交叉位置上的基因外剩余部分的基因填充，具体见表1。

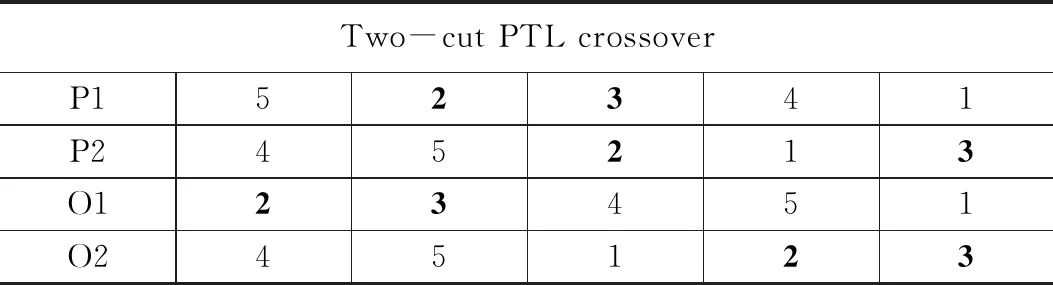
表1 PTL交叉因子的一个例子

为了保证所得解的多样性，交叉操作之后，对生成的子代进行变异操作，本文采用单点变异法，变异位置是随机生成的。

选择：选择是根据适应度函数或者序值进行交叉操作父代选择的一个过程。在这个过程中本文应用锦标赛父代选择法，这是遗传算法所有选择方法中的一种。锦标赛选择法是随机选择一些解，然后根据序值选择其中最好的作为交叉操作的父代。

停止标准：本文中的停止标准是设定一个比较大的迭代次数。

2.3 L-NSGA算法

L-NSGA算法和NSGA-II算法结构类似，唯一不同之处在于：L-NSGA算法是基于Lorenz支配关系的，而NSGA-II算法则是基于Pareto支配关系。对于本文，带有机器人制造单元的作业车间调度最小化工件完工提前量和延迟量的总权重的一个双目标优化问题，如果f1(x)>f2(x)，则X的Lorenz矢量为:

L(x)=(f1(x),f1(x)+f2(x))

(10)

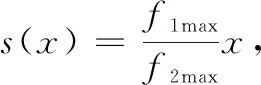
2.4 CDAS-NSGA算法

同样CDAS-NSGA算法和NSGA-II算法的结构也类似，CDAS-NSGA算法是基于CDAS支配关系进行解的排序。经CDAS标准修改每一个目标函数的适应度值，从而扩大或者缩小解的支配领域。

在CDAS-NSGA算法中，我们同样也应用了动态线性比例函数，具体和2.3节L-NSGA算法中提到的一样。

3 实验结果与分析

3.1 仿真测试介绍

本文算法以Visual Studio 2017开发工具编程实现。选取了16组实例数据进行实验，其中实例1～8参考Caumond[22]论文中的数据，实例9～15自己生成的。每个实例包含不同数目的工件、机器与加工工序。参数aj和bj根据完工时间按照一定规律随机产生。分别利用NSGA-II、L-NSGA、CDAS-NSGA算法对该问题进行最优解的寻求。其中交叉概率Pc设为0.9，变异概率Pm设为0.1，迭代次数设为20，种群大小设为40，CDAS-NSGA中的用户自定义参数S设为0.45。每个实例数据测试20次，记录每种支配方式最后找到的非支配解。

3.2 对比准则

由于每一个Pareto 前端不是一个单独的解，而是一个非支配解的集合，所以对于两个不同的Pareto前端的比较是困难的。我们的目地是让生成的解的多样性最大化，Pareto优化解之间的绝对距离最小化，包含前端的伸展性最大化。本文采用由Dugardin等人提出的μd距离法和Zitzler 和Thiele 提出的C比较准则。

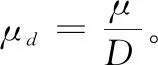
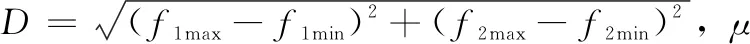
3.3 实验结果与分析

为了分析比较不同的支配关系对单机器搬运的柔性作业车间调度问题求解的效果，我们分别通过μd距离法和C准则对所得非支配解进行比较分析。具体数据如表2，表3，表4所示：其中表2是L-NSGA算法与NSGA-II算法最优解之间的比较，表3是CDAS-NSGA与NSGA-II最优解之间的比较，表4是CDAS-NSGA算法与L-NSGA算法最优解之间的比较。以表2第一行例LT155为例：机器数为5，加工工件数为3，μd为L-NSGA算法所得的“最优解”相对于NSGA-II算法中所有“最优解”比较后的平均μd距离，μd=-0.006 9<0,μd的最优值代表L-NSGA所得的解大多数位于NSGA-II的下方，说明L-NSGA所得解更优，分别代表该组最好的距离。C1代表L-NSGA算法所得的解被NSGA-II支配的概率，表中平均C1=0.15，代表L-NSGA中15%解被NSGA-II中的解支配，同理C2代表NSGA-II中的解被L-NSGA中的解支配的概率，C2=0.29,说明NSGA-II中29%的解被L-NSGA中的解支配。

从表2表3中，我们看到的值都是负的，而且大部分的C1值小于C2的值，说明基于lorenz支配关系和基于CDAS支配关系所得的解明显优于基于Pareto支配关系所得的解。

表4中的值大部分都是正的只有少数是负的，且在在这些事例中C1平均值基本大于C2的平均值值，说明在参数S为0.45时基于lorenz支配关系所得的解明显优于基于CDAS支配关系所得的解。

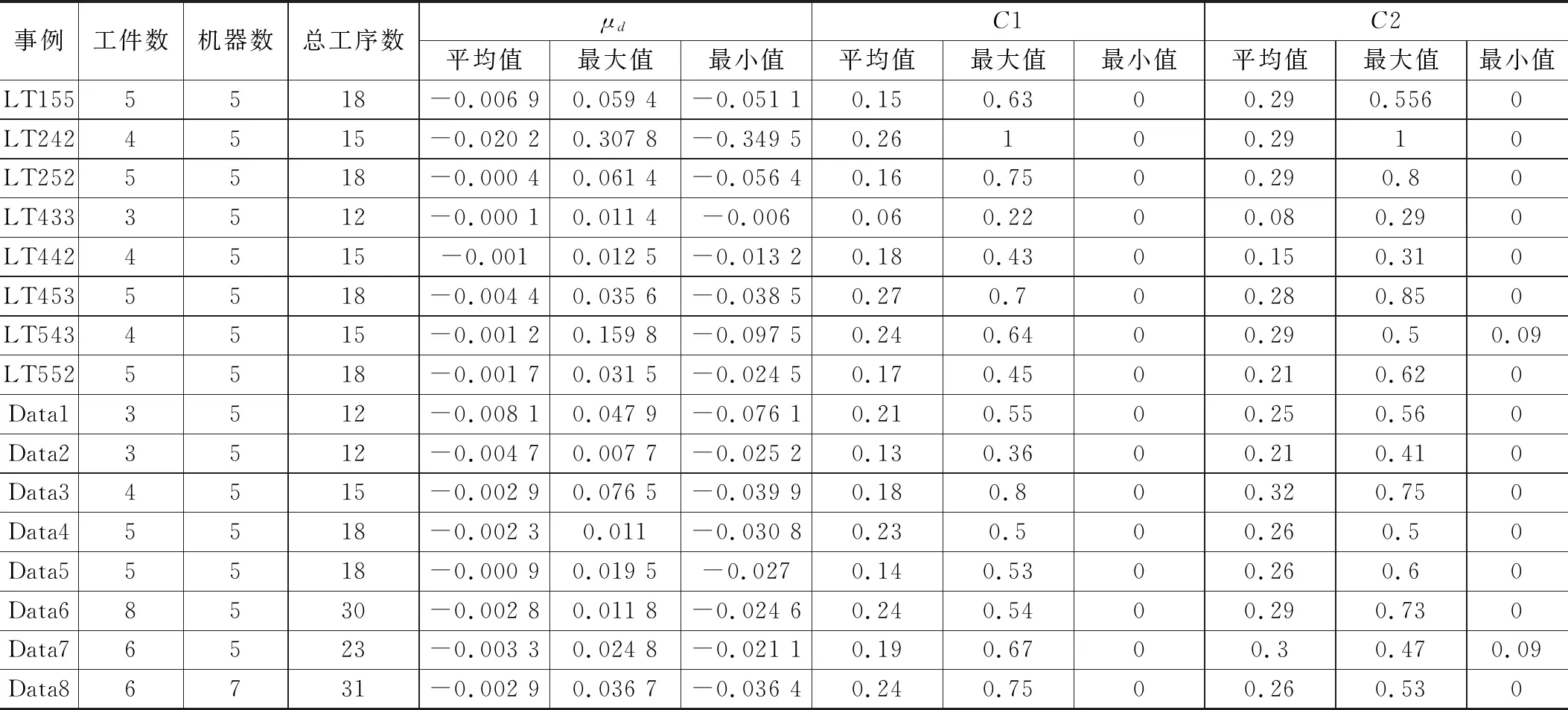
表2 L-NSGA算法与NSGA-II算法比较结果

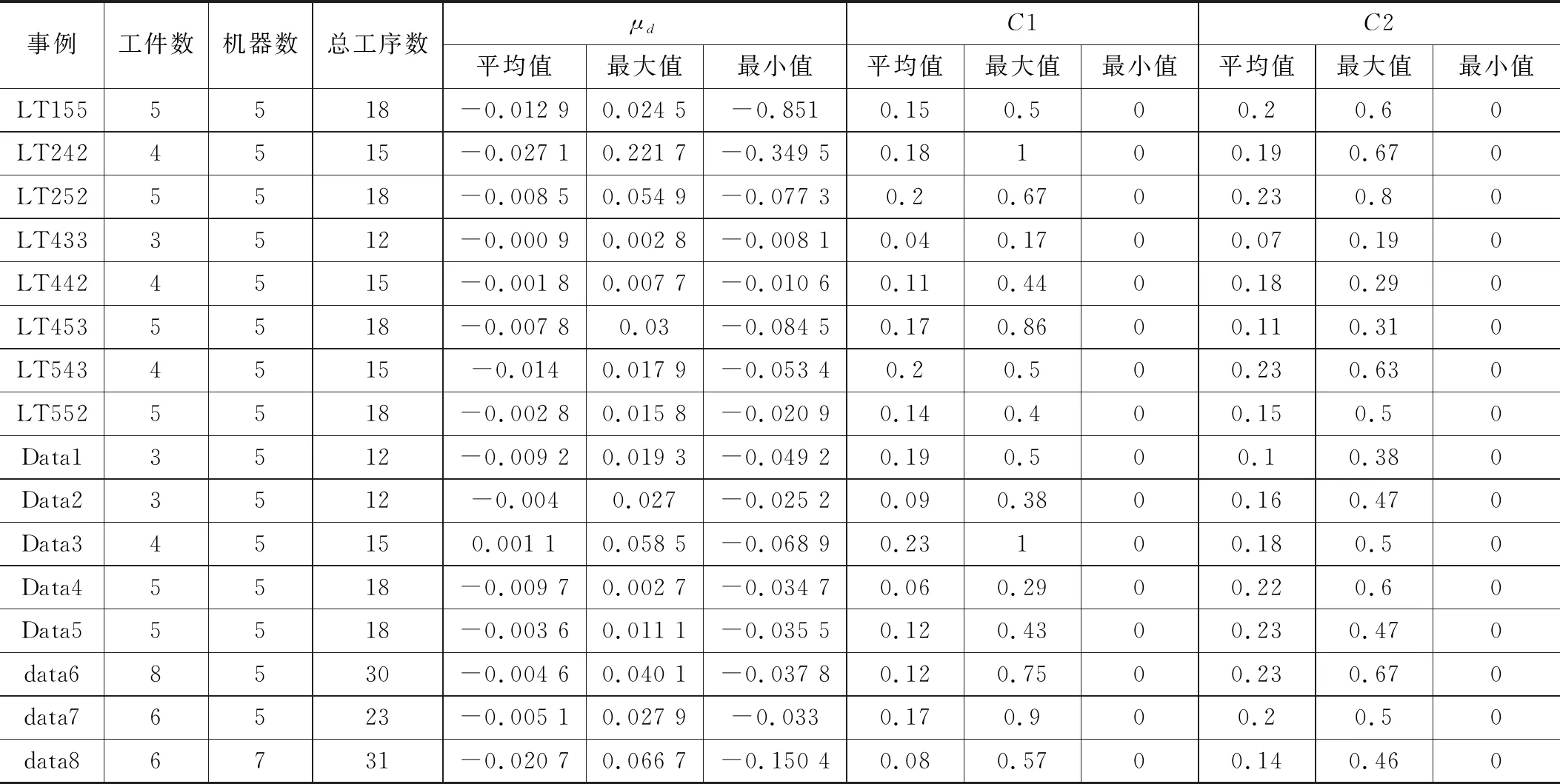
表3 CDAS-NSGA算法与NSGA-II算法比较结果

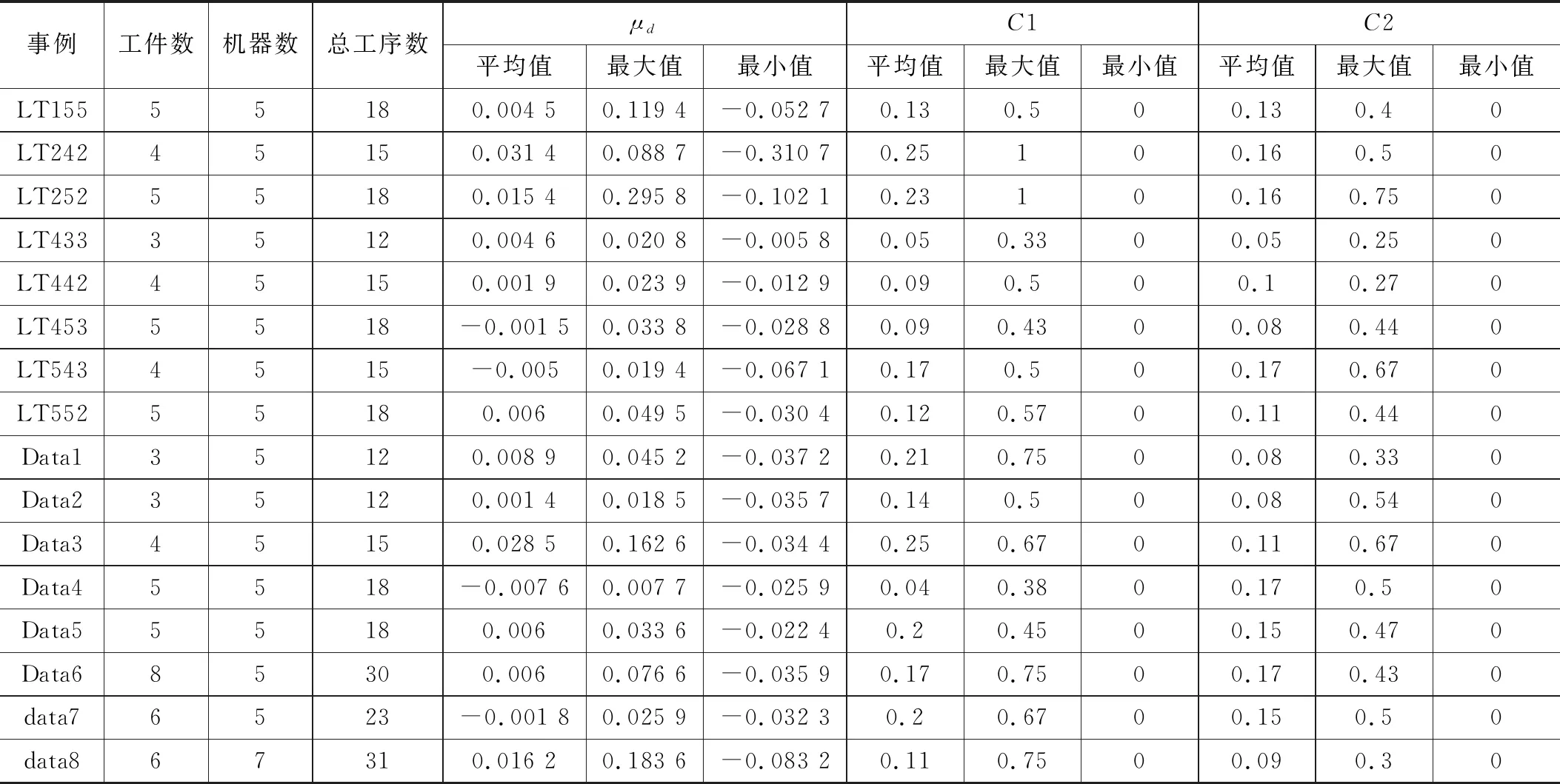
表4 CDAS-NSGA算法与L-NSGA算法比较结果

4 结束语

本文我们研究了一个带有单机器人制造单元的作业车间调度问题的优化问题。大量研究表明，改变支配关系可以有效提高算法寻求最优解的效率，Lorenz支配关系与CDAS支配关系的支配区域都比Pareto支配关系的支配区域大，则这两种支配关系下找到的非支配平面的最优解集是Pareto支配关系下找到的非支配平面的最优解集的子集。文中我们将以NSGA-II为框架结合Lorenz支配关系和CDAS支配关系并与传统的基于Pareto支配关系的NSGA-II3种算法去研究同一优化调度问题，最后将3种算法所得的非支配解通过C准则和准则进行比较分析，我们发现对于求解高维多目标优化问题，基于Lorenz支配关系和CDAS支配关系的优化算法比基于传统的Pareto支配关系的优化算法的效果更佳。在CDAS支配关系中当S值为0.45时，基于CDAS支配关系的优化算法明显比基于Lorenz支配关系的优化算法差。