基于深神经网络的线性回波抵消与不完全传递函数的凸重构

(华池县职业中等专业学校，甘肃 华池 745600)

0 引言

在语音通信、数据通信等领域中，都不同程度地存在回波问题，回波的存在影响了通信质量，严重时会使通信系统不能正常工作[1]。因此，必须采取有效措施来抑制回波，消除其影响。回波消除是通常采用的基本方法，其基本思想是估计回波路径的特征参数，产生一个模拟的回波路径，得出模拟回波信号，从接收信号中减去该信号，实现回波消除[2]。但是，在逼近信号(语音)活跃的情况下，使用线性回波消除方法来消除回波是比较困难的。

然而，根据现有研究现状，对于稀疏脉冲响应在时间频率域中的修正，还没有相关的研究工作。因此，在时频域中研究稀疏脉冲响应的修正，在许多应用中具有很好的研究意义[3]。本文提出了适用于频域痉挛脉冲响应的LMS方法。当标签信号处于激活状态时，基于LMS的算法的性能会下降。因此，将该算法与语音活动检测(VAD)结合使用，当目标信号激活时，LMS的自适应停止[4]。另一种解决方案采用盲源分离方法，旨在跟踪目标信号活动在期间H(n)的变化。

在本文中结合了两种观点：一种观点是使用一个在混合信号上训练的深神经网络(DNN)来执行一个与频率相关的VAD；另一种观点是，在与H(n)相关的频域中，只有在目标信号不活跃的频率箱中才能观测到传输。因此，本文采用基于DNN的VAD，它决定了目标信号(语音)占主导地位的频率。然后，将LMS应用于只受干扰的频率，由此得到不完全传递函数(ITF)，ITF是使用基于凸重构的方法完成。从而实现基于深神经网络的线性回波消除，得到基于凸重构的不完全传递函数。

1 方法论

为了解决回波消除(AEC)的问题，可将该问题表述为传声器x(n)上的信号传播时，对噪声参考信号r(n)与干扰(噪声)源与传声器之间的声脉冲响应h(n)的估计，s(n)可以通过观察得到[5]。当目标源(通常是说话人)处于活动状态时，在间隔期间估计是较困难，模型在时间域中，描述为式(1)：

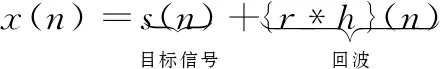
(1)

式中，*表示卷积。获得了h(n)的估计值，即模拟回波信号，就可以从接收信号中减去该信号，实现回波消除。增强型麦克风信号如式(2)、式(3)所示：

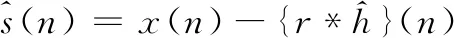
(2)

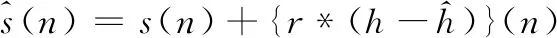
(3)

在上式中，干扰源和麦克风可以改变位置。必须对问题进行自适应处理。为此，在时间域或频率域中应用自适应最小均方算法(LMS)。由于该算法结构简单，性能稳定，计算复杂度低，在回声消除领域被广泛应用[6]。但是当信号相关性较大时，LMS算法的收敛性很差。文献[7]中提出了对稀疏脉冲响应的线性矩阵进行时域修正的方法，如比例归一化线性矩阵(PNLMS)。PNLMS算法采用不同的步长与估计的滤波系数成比例，具有很快的初始收敛速度。此外，也出现了许多对PNLMS的改进，如改进的PNLMS(IPNLMS)或重新加权零校正PNLMS(RA-PNLMS)[8]，IPNLMS用于提高PNLMS算法在非稀疏回声路径下的性能。

最小均方(LMS)适用于这些问题，需要估计脉冲响应的地方[9]。这种计算的理想条件是目标信号s无效,然后准确估计脉冲响应。

可以最小化均方误差区间n=n1，…，n2。Jn(h)标准均值可以如式(4)最小化：

(4)

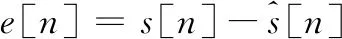
(5)

梯度ΔJn(h)可以表示为式(6)，其中Wn，bn分别用式(7)、(8)表示：

ΔJn(h)=-2bn+2Wnh

(6)

(7)

(8)

令ΔJn(h)等于零，则存在Wn的逆矩阵，得到式(9)：

(9)

AEC问题的时频域(FDLMS)中的LMS可表示为式(10):

(10)

其中:Xn,γ与Rn,γ分别是短时傅里叶变换(STFT)中的混合信号和参考信号。下标n表示帧号，γ表示频率仓。表达式(10)中定义的LMS的解可以通过如下计算参考信号和混合信号之间的相互关联来完成，如式(11)：

(11)

间隔n和频率仓γ上的参考信号的自相关系数由下式给出：

(12)

环境的传递函数由式(13)给出：

(13)

然而，自适应间隔越短，连续数据变化越大。如果块太短，则W接近单数。为此，提出了自适应LMS算法。自适应LMS的目的是用于脉冲响应估计，使第n帧中的实际误差最小化。

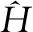
(14)

改进自适应传递函数为式(15)：

(15)

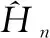
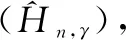
(16)

1.1 最大算子

逼近算法是解决凸问题的有力工具[12]，如式(16)所示。提出了2种基于逼近算法的改进型。算法的投影算子定义为式(17)。

(17)

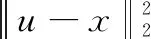
1.2 最大梯度法

为了制定逼近梯度法，需要考虑以下分裂问题：

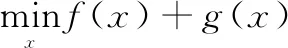
(18)

其中:f(x)函数和g(x)函数是闭函数，f(x)函数适当的凸函数且可微，f(x)是凸函数但在某些地方不可微。式(18)的逼近梯度法的一次迭代如式(19)：

x=proxλg(x-u▽f(x))

(19)

(20)

其中:参数λ与式(15)中的a紧密相关。对式(16)的逼近梯度算法的改进后如式(21)所示：

(21)

综上，本文提出的梯度算法过程如下算法1所示：

Algorithm 1:Proposed gradient based method

Input:X,R,O= {r1,…,r|o|},μ,λ,

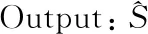
initialize:H←0,Hold←0

forn=1 toNdo

En,o=Xn,o-Rn,oHold

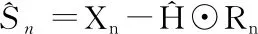
end

1.3 乘子变换方向法

交替方向乘法器(ADMM)是求解凸问题的一种快速而鲁棒的方法[13]。为了构造ADMM，需要将式(18)中定义的拆分问题重新表述如式(22)所示：

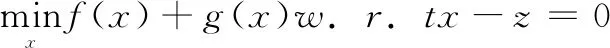
(22)

其中:f(x)函数和g(x)函数是闭函数，f(x)函数适当的凸函数且可微，g(x)是凸函数但在某些地方不可微。公式(22)的增广拉格朗日如下：

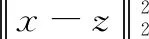
(23)

其中:u是与等式约束相关联的双可用性，p是一个正参数。ADMM可以用式(23)中固定z值改变x来表示最小值，反之亦然。因此，ADMM的改进顺序如下：

x=proxuf(z-u)

z=proxλg(x+u)

u=u+ρ(x-z)

(24)

(25)

其中:μ>0为阶梯尺寸参数，λ>0控制解的稀疏度，ρ为0.95。

综上，本文提出的乘子变换方向法的算法过程如下算法2所示：

Algorithm 2 Proposed ADMM based method

Input: X, R, O = {r1,…,r|o|},μ,ρ,λ,

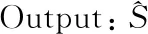
initialize: H←0,Hold←0, U←0, Uold←0

for n=1 to N do

En,o=Xn,o-Rn,o(Hold-U)

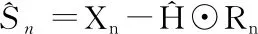
end

2 结果与讨论

2.1 频域语音活动检测

功率谱密度是一种概率统计方法，是对随机变量均方值的量度[14]。因此，对于频域语音活动检测，一个有效的方法是根据混合信号的功率谱密度(PSD)来检测最活跃的频率[15]。选择最活跃频率的分位数，如果所选频率的百分比设置为100%，则占用整个带宽。如果将其设置为其他值(如40%)，那么整个带宽中只有不到一半的频率箱是最活跃的。

深度神经网络(DNN)，是一种判别模型[16]。即已知变量x，通过判别模型可以推算出y；深度指的是一系列连续的表示层，通过这些层可以对数据进行高层次的抽象，其具备至少一个隐藏层；可以使用反向传播算法进行训练，使用梯度下降求解神经元之间的权重[17]。因此，采用深度神经网络(DNN)对信号噪声比(SNR)大于5 dB的频谱仓进行估计。汉明窗计算分析信号谱图，相关信号信息见表1。训练数据包括70 h中央人民广播电台的主持人讲话和中国古典演奏音乐样本(混合样本的全球信噪比在-5～10 db之间变化)。编制输出标签(信噪比小于5 db为0，其余为1)，计算输入数据的零均值和单位方差归一化统计。

改进的DNN由输入层(2 049个神经元)、2个隐藏层(4 000和3 000个神经元的宽度)和输出层(2 049个神经元)组成。层间的激活函数采用ReLU；输出层包含Sigmoid激活函数。优化标准为MSE，批量为1 024个样品，倾斜率为0.015。

2.2 仿真结果

在AEC环境下评估所提出算法性能的仿真结果。在实验中，模拟了目标信号s(n)，其来源是一个连续的女性语音作为逼近，而r(n)是音乐或白噪声，代表远端信号。具体实验信号配置如表1所示。

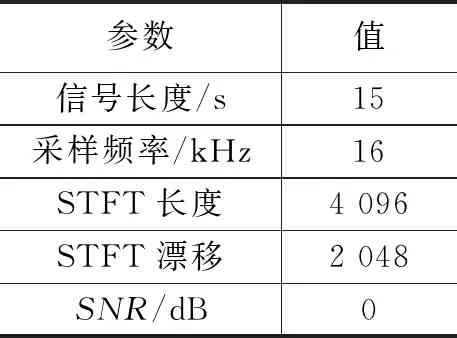
表1 信号基本信息

脉冲响应由房间尺寸为5 m×4 m×6 m的房间脉冲响应(RIR)发生器生成。源位置设置为[2,2.5,2]m，麦克风位于[2,3.5,2]m。每个生成的脉冲响应的长度h(n)为4 096个样本。脉冲响应稀疏产生，因此其他参数设置如表2所示。

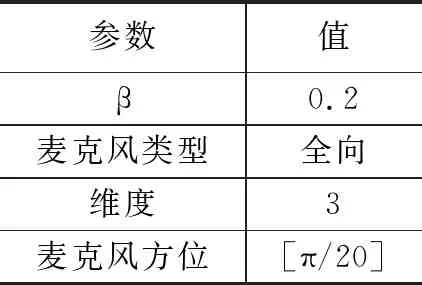
表2 脉冲响应参数设置

第一个实验使用4个语音进行，第二个实验是对20种语言和音乐的混合进行评估，两个实验的结果均在混合物上取平均值。我们将提出的算法与其他已知算法(IPNLMS和FDLMS)的收敛速度进行了比较。通过归一化偏差测量收敛速度，其定义如下：

(26)

其中:n是帧索引。在实验中，通过将第60帧处估计的脉冲响应归零来模拟脉冲响应的变化。

2.2.1 白高斯噪声实验

白高斯噪声，幅度分布服从高斯分布，功率谱密度服从均匀分布，即任意时刻的噪声值都是随机的，在时间轴的某点上，噪声孤立，不受前后点噪声幅值影响[18]。图1展示了白高斯噪声的功率分布情况，从图中可以看出其功率谱密度服从均匀分布，符合上述实验需求。

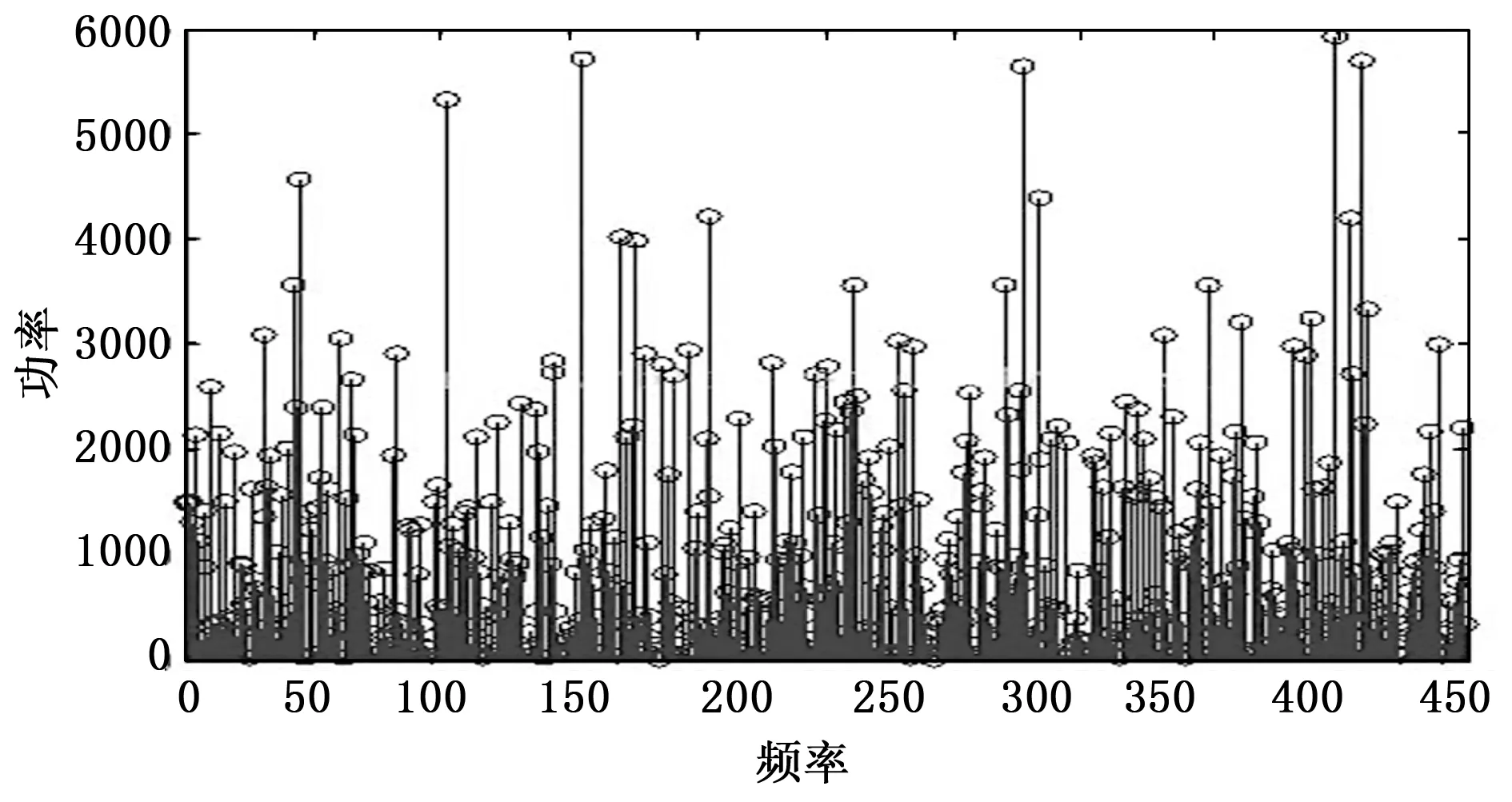
图1 白高斯噪声功率谱

同时，对白高斯噪声下的LMS进行测试，观察算法迭代次数对结果的影响。

图2 白高斯噪声下的LMS

从图2中可以看出，随着算法迭代次数的增加，均方误差(MSE)递减，表示算法估计值与真值之差平方的期望值。这说明高迭代计算中，LMS算法的学习效果更好。因此，后续试验设置迭代次数为600，以保证实验精确性。

基于白高斯噪声对多种算法进行比较，算法比较的详细设置如表3所示。本实验进行了3种变体，表3为白噪声实验中的算法设置。

在每种变体中，考虑了不同百分比的活跃频率值，即40%、60%和80%，其中IPNLMS算法使用100%。

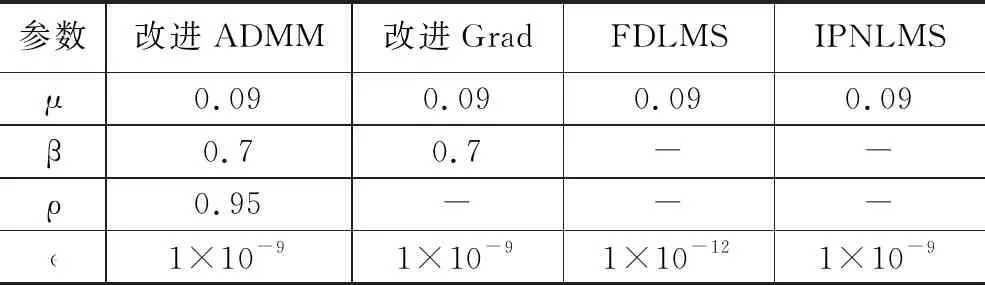
表3 白噪声实验中的算法设置

其中40%的频率箱用于FDLMS和改进算法，图3表明，IPNLMS的收敛速度比所改进的方法快40%左右。在图4中，当使用的频率箱数为60%时，所改进算法收敛更快，并且它们收敛到与IPNLMS相同的解；在图5中展示了频率箱数为80%的收敛结果。通过实验可以得出，在活跃频率为80%时，本文算法取得较好的效果。

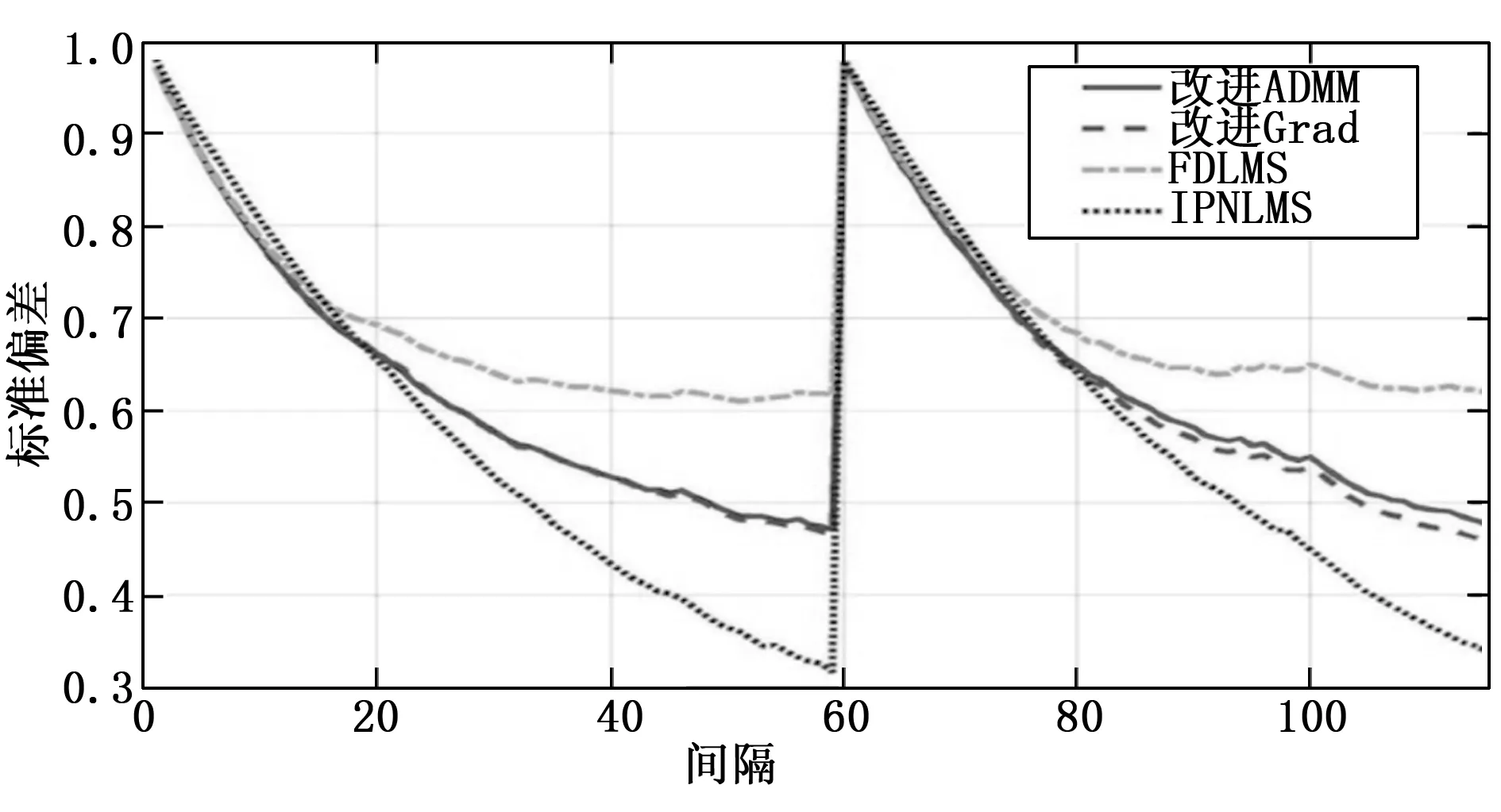
图3 40%频率箱条件下不同算法收敛速度比较

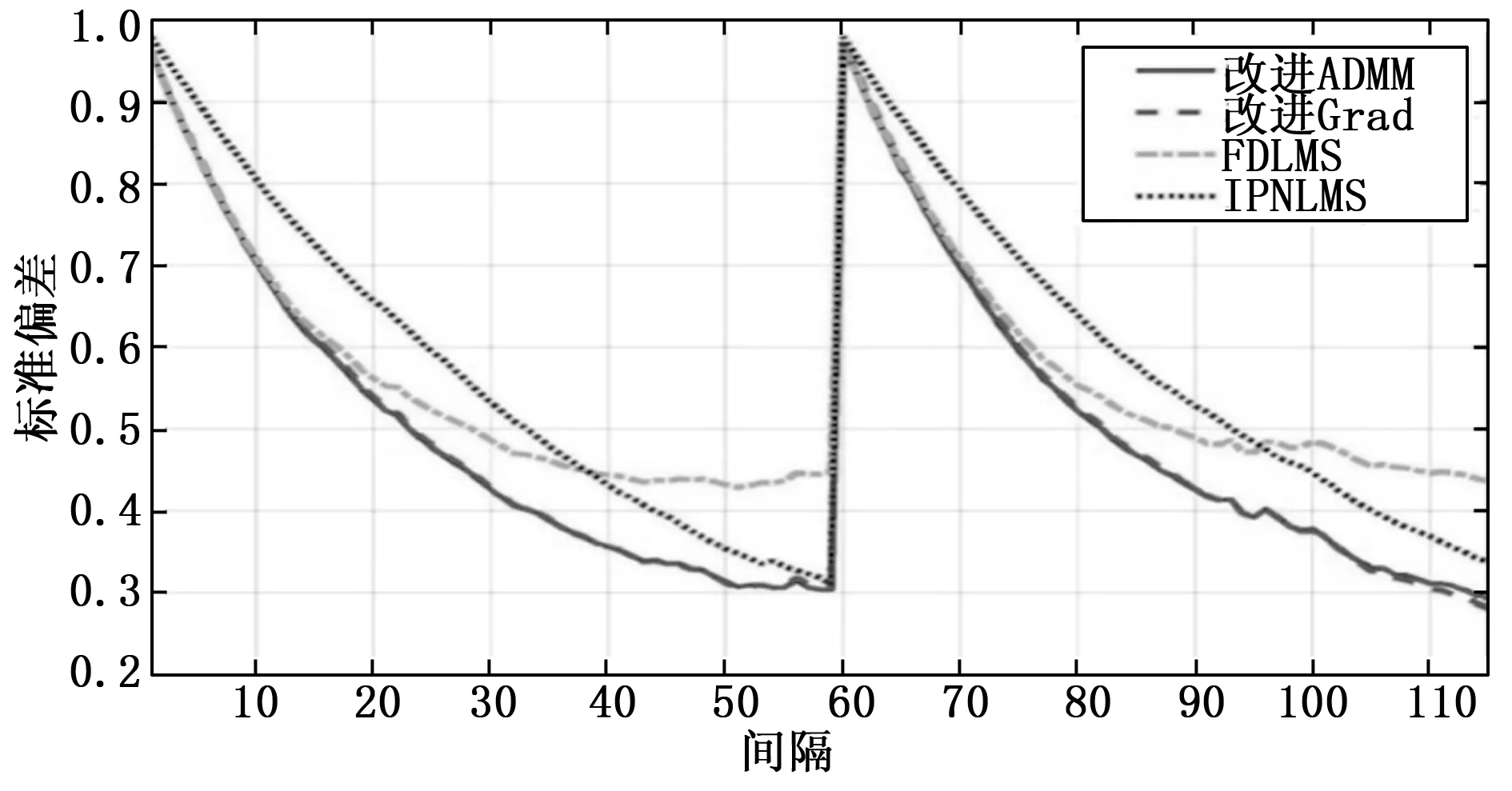
图4 60%频率箱条件下不同算法收敛速度比较

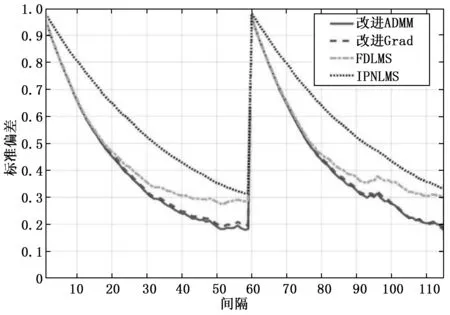
图5 80%频率箱条件下不同算法收敛速度比较

2.2.2 语音实验

对20种语言和音乐的混合语音信号进行实验，详细实验设置如表4所示。

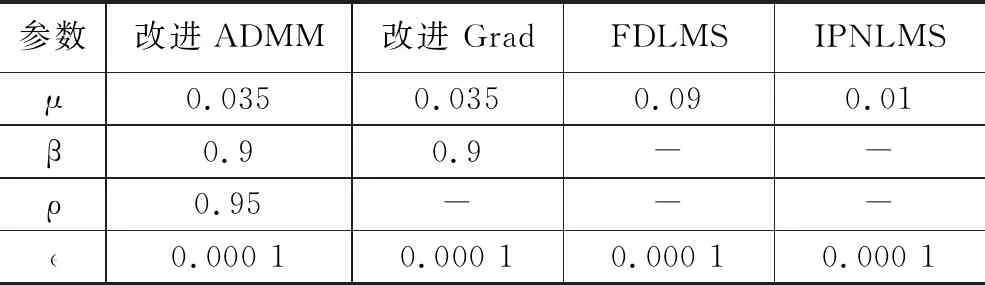
表4 音乐实验中的算法设置

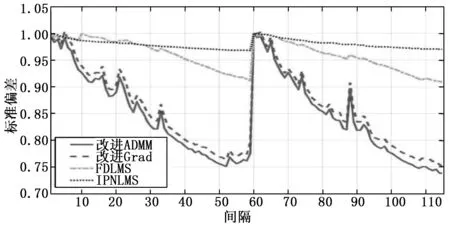
图6 使用DNN的收敛速度

从图6中可知，因为IPNLMS无法估计存在串扰时的脉冲响应，因此获得最差的收敛性能。FDLMS也会缓慢收敛，而且不能达到很好的精度。相比之下，本文提出的算法收敛速度快，且实现的精度高。

2.2.3 计算时间

表5显示了每个算法处理混合声音所花费的平均时间，值为两个实验的平均值。实验使用Matlab 2016b软件，在基于Intel核心IS-4440的PC机上进行。

表5 不同算法的花费时间 s

3 结束语

本文基于深度神经网络的特性，提出了两种解决问题的新算法：一种基于逼近梯度法，另一种基于交替方向乘法器。同时，本文方法基于不完全自适应LMS和逼近算法的范数重构实现，用于解决线性回波消除问题。基于高斯白噪声及多音源混合语音信号进行算法验证。结果表明，对于用于不完全传递函数估计的合适频率段百分比，该方法比其他常用算法收敛速度更快；同时，本文所提出的方法所需的平均计算时间也比其他常用方法要短。为语音传输业务中存在回声消除问题提供了新思路。