基于浸入—不变集的三旋翼无人机高度系统自适应控制器设计

(1.天津航天中为数据系统科技有限公司，天津 300301;2.滨州学院 飞行学院，山东 滨州 256600)

0 引言

随着智能控制技术和传感器技术的快速发展，无人机在军用和民用领域得到了广泛的关注和研究。近年来，多旋翼无人机在敌情侦测、航空摄影、灾后救援、快递运送等军事和民用领域得到了广泛的应用[1-2]。与传统的四旋翼无人机、六旋翼无人机不同，三旋翼无人机作为一种特殊构型多旋翼无人机，其动力机构主要包括三个电机和一个可偏转舵机[3]。因此，其具有结构紧凑、飞行功耗低、机动性能好等优点，应用前景广阔。

针对三旋翼无人机，目前已有国内外多家科研机构开展了相关研究。Lozano教授团队主要对三旋翼无人机动力学建模及位姿控制进行了研究。文献[4]对力和力矩产生的原理进行了分析，设计了基于饱和函数的连续控制策略用于实现三旋翼无人机的位姿增稳控制，并在基于xPC的硬件在环仿真平台上进行了飞行实验。文献[5]考虑系统耦合与反扭矩影响，提出了一种鲁棒控制律，并在三旋翼无人机上进行了飞行实验验证。爱沙尼亚塔林理工大学的研究人员为了提高三旋翼无人机的自主飞行程度，根据飞行初始阶段与最终阶段对无人机动力学变化及其性能要求的不同，设计了两个阶段的自主控制程序，并通过数值仿真进行了验证[6]。波兰西里西亚工业大学的研究人员采用三个电机和一个可偏转舵机设计了三旋翼无人机。文献[7]对力矩作用原理、动力学特性及机载测量单元和滤波系统进行了分析，然后设计了基于扩展卡尔曼滤波的导航算法，最后基于PID控制器进行了轨迹跟踪实验验证。

国内方面，南京航空航天大学的研究人员针对倾转尾翼式三旋翼无人机的姿态和高度控制提出了一种基于模糊规则、极点配置、跟踪控制的自适应混合策略[8]。控制器增益整定通过自适应模糊逻辑控制器实现，并通过数值仿真进行了验证。文献[9]在文献[8]的基础上，将基于模糊规则的RST控制器与模型参考自适应算法相结合，实现了三旋翼无人机的姿态和高度控制。数值仿真结果表明，与已有自适应RST 控制器相比，该算法具有暂态性能较好、稳态误差小、切收敛速度快等优点。中国科学院长春光学精密机械与物理研究所和长春理工大学的研究人员合作，对三旋翼无人机的机械结构、数学模型、控制器设计等进行了研究，分别采用PID 控制算法和线性二次高斯(LQG)控制方法设计了姿态控制器[10]。西北工业大学的研究人员对倾转尾翼式三旋翼无人机的着舰运动进行了研究。针对船舰甲板运动对无人机着舰的影响，采用改进PD 控制器分别对甲板沉浮及横摇进行了补偿和预估。数值仿真结果表明所提控制方案满足着舰要求[11]。文献[12]研究了倾转式三旋翼无人机数学建模和控制律设计问题，设计了针对倾转式三旋翼无人机的位置非线性控制器和姿态及高度的非线性自适应控制器，通过实验仿真平台验证了所设计控制律的鲁棒性与有效性。

综上所述，针对三旋翼无人机的研究仍处于起步阶段，研究内容集中于数学模型分析、简单的控制算法设计等内容。本文将针对三旋翼无人机的动力学建模和高度控制进行研究，采用基于浸入—不变集的新型自适应控制器进行高度控制器设计，并对未知空气阻尼系数进行在线估计，并通过硬件在环仿真实验进行实时实验验证。

1 动力学模型分析

为了便于对三旋翼无人机进行动力学模型分析，首先进行坐标系定义，分别是惯性坐标系{I}和体坐标系{B}，其中惯性坐标系{I}采用本地NED(北东地)坐标系统，原点固定于地面，体坐标系{B}采用机载NED坐标系统，原点固定于无人机重心，如图1所示。

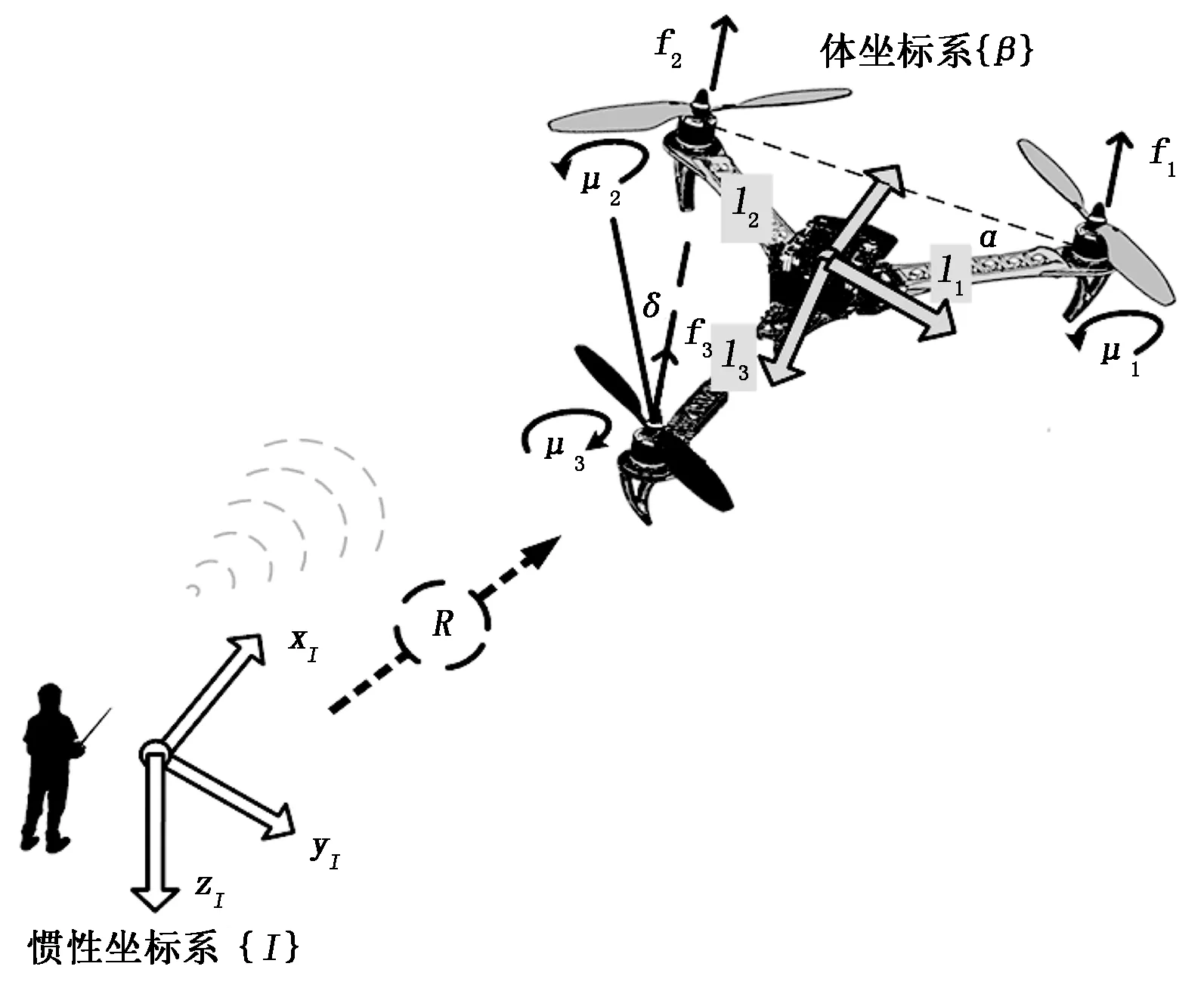
图1 三旋翼无人机坐标系

在图1中，{xI,yI,zI}和{xB,yB,zB}分别表示惯性坐标系{I}和体坐标系{B}各轴正方向上的单位向量，f1,f2,f3分别表示3个电机产生的升力，l1,l2,l3分别表示1号电机、2号电机、3号电机到坐标原点的距离，且满足l1=l2=l，α为1号电机与2号电机连线和1号电机与坐标原点连线之间的夹角，δ(t)为尾部舵机偏离XOZ平面的角度，顺时针为正。采用欧拉角法进行姿态表示，综合考虑空气阻尼系数的影响，得到惯性坐标系{I}下三旋翼无人机姿态系统和高度系统的动力学模型为：

(1)

其中:φ(t),θ(t),ψ(t),z(t)分别表示三旋翼无人机的滚转角、俯仰角、偏航角和高度，m为其质量，Ji,i=1,2,3为其转动惯量，kφ,kθ,kψ,kz分别表示滚转通道、俯仰通道、偏航通道和高度通道的空气阻尼系数，dφ(t),dθ(t),dψ(t),dz(t)分别为滚转通道、俯仰通道、偏航通道和高度通道的外部扰动力矩，g为重力加速度，τφ(t),τθ(t),τψ(t)分别为滚转通道、俯仰通道、偏航通道的输入力矩，T(t)为各电机产生的总升力。在后续讨论中，参数kz,kφ,kθ,kψ,dφ(t),dθ(t),dψ(t)假设为未知。

在图1中，控制输入力矩及总升力与各电机升力及舵机角度之间的关系可以表示为：

(2)

其中:k1,k2,k3表示反扭力系数。

考虑无人机实际飞行情况，作出如下假设：

假设1：

-π/2<φ(t)<π/2,-π/2<θ(t)<π/2。

假设2：

三个电机参数完全相同，则k1=k2=k3=k。

假设3：

由于尾部舵机偏转角度变化范围很小，通常小于8°，sinδ≼cosδ，因此k3f3sinδ可以忽略。

应用假设2和假设3，式(2)可以改写为：

(3)

式(3)即为三旋翼无人机姿态系统和高度系统的动力学模型。本文的主要研究目标是控制三旋翼无人机的高度跟踪目标高度zd(t)。

2 控制器设计

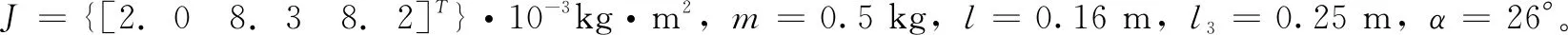
定义高度控制误差ez(t)∈R为：

ez=zd-z

(4)

定义滤波误差信号rz(t)∈R为：

(5)

其中:αz为正常数。因此，

(6)

对式(5)求取一阶时间导数，并将式(6)代入整理得：

(7)

(8)

其中:βz(ez,rz)∈R为连续辅助函数。对式(8)求取一阶时间导数，并将式(6)和式(7)代入，整理可得：

(9)

(10)

设计控制输入T(t)为：

(11)

其中:kr,kez均为正常数增益。辅助函数βz(ez,rz)设计为：

(12)

其中:γz为正常数。将式(10)～(12)代入式(9)，整理得：

(13)

将式(11)代入式(7)，整理可得：

(14)

定理1：针对系统(7)，设计式(11)所示的控制器、式(10)所示的自适应律和式(12)所示的辅助函数，则闭环系统(14)渐近稳定，即：

(15)

证明：定义Lyapunov候选函数Vz∈R为：

(16)

对Vz(t)求取一阶时间导数，并将式(6)、式(13)及式(14)代入，整理可得：

2kezez(-αzez+rz)+2rz(-krrz-

(17)

由式(16) 和不等式(17) 可得，闭环系统的所有信号收敛于不变集：

(18)

定理1得证。

当在实验平台上对控制策略进行实现时，将式(12)代入式(10)及式(11)中，整理得到各参数的表达形式如下：

(19)

3 实验验证与结果分析

为了对所设计控制算法的有效性进行验证，采用自主设计的三旋翼无人机硬件在环仿真平台进行了实验验证。所设计控制器中各参数选择如前所述：J={[2.0 8.3 8.2]T}·10-3kg·m2，m=0.5 kg，l=0.16 m，l3=0.25 m，α=26°，αz=0.3，kr=0.3，γz=0.5。高度跟踪目标设定为：zd=2 m。采用本章所设计控制器进行高度控制的实验结果如图2～4所示。

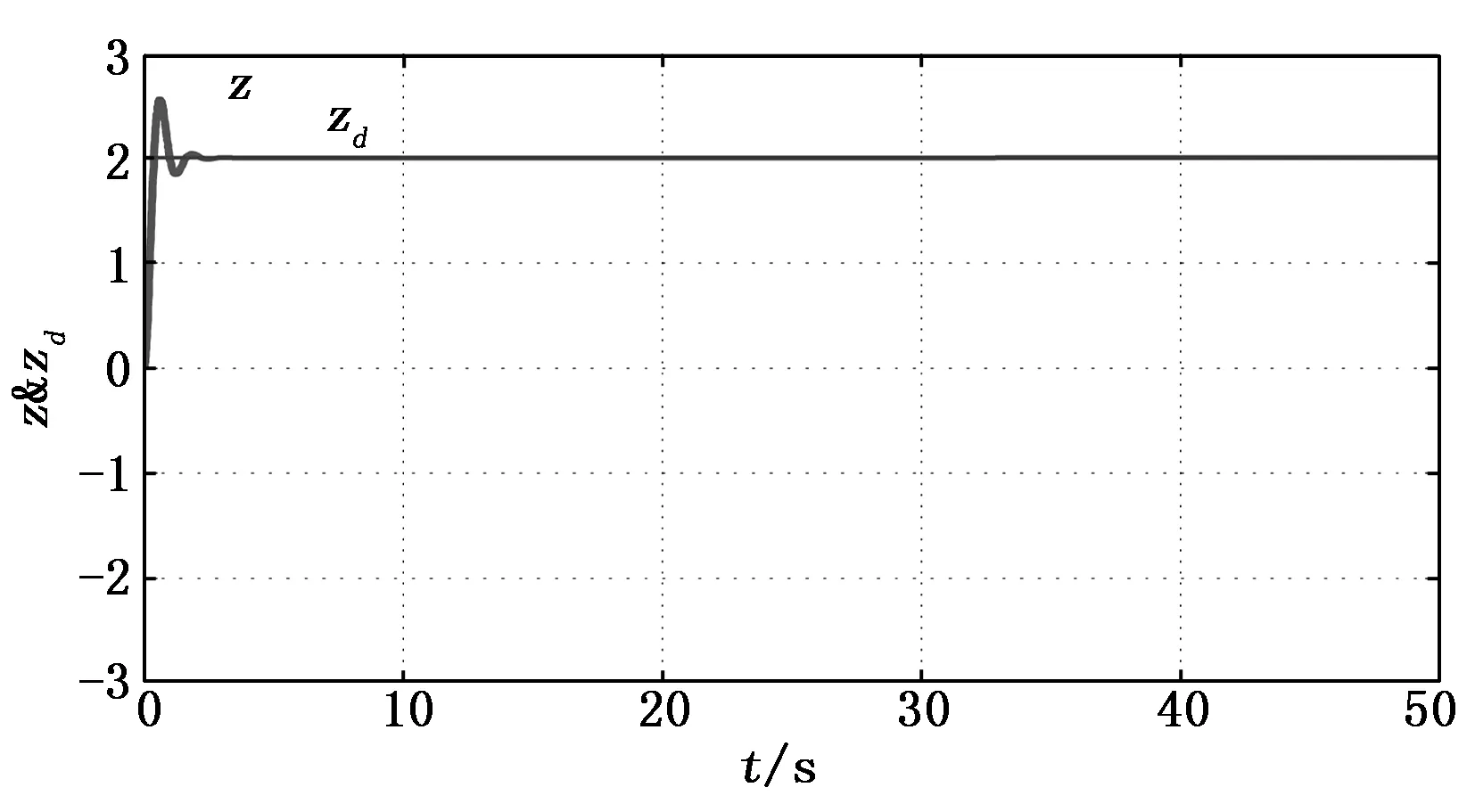
图2 当前高度与目标高度变化曲线

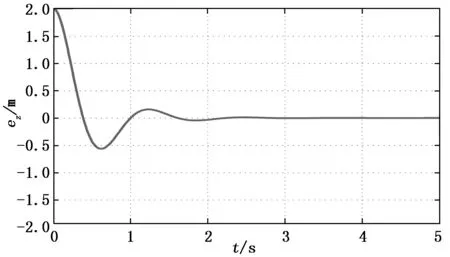
图3 高度跟踪误差变化曲线(0-6秒)

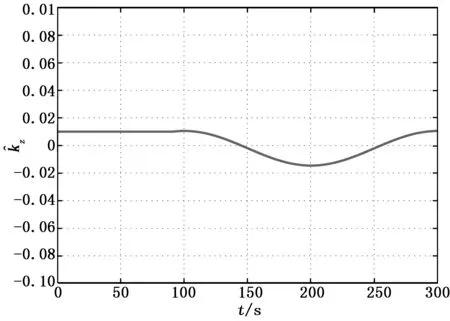
图4 控制阻尼系数估计值变化曲线

图2中曲线分别表示当前高度和目标高度的变化曲线，当前高度由加速度积分得到。从曲线中可以看出当前高度能够较快的与目标高度达到吻合。图3为高度跟踪误差在0～6 s的变化曲线，能够清楚地表示高度跟踪误差在2秒左右收敛于稳定值0的过程。图4为控制阻尼系数估计值的变化曲线，能够在较短时间内较好地收敛于合理的范围，表明所设计的控制器算法稳态误差小，收敛速度快，具有较好的控制性能。

4 结束语

本文对三旋翼无人机的动力学建模和高度系统的控制问题进行了研究。设计了基于浸入—不变集的自适应算法实现了对高度的跟踪控制，并对未知空气阻尼进行了有效估计。对于所设计控制算法的稳定性，采用基于Lyapunov的分析方法进行了证明。在自主设计的三旋翼无人机硬件在环仿真平台上对所提控制策略进行了实验验证。结果表明高度跟踪误差在0～6 s可较好地趋于收敛，控制阻尼系数估计值也较好地收敛于合理的范围，所设计控制算法具有较好的控制性能和较强的实用性能。