基于VBEM的ARFA模型参数推导和故障检测

李吉俊 章智杰 李其操 董自健

摘  要：文章使用自回归因子分析模型（ARFA）對数据样本进行动态过程建模，分析了卡尔曼滤波和EM算法在估计ARFA模型中回归矩阵参数A和载荷矩阵参数C的方法。在此基础上，提出了一种使用变分贝叶斯EM（VBEM）故障检测方法，对ARFA模型参数A和C进行推断和动态过程故障检测。仿真实验结果表明，在ARFA模型下，VBEM方法对下文所述的阶跃信号、斜坡信号等四类故障的检测效果要优于EM方法对该类故障的检测效果，并且降低了平均迭代次数。

关键词：自回归因子分析模型;EM算法;变分贝叶斯EM;故障检测

中图分类号：TP277;TP391.9      文献标识码：A 文章编号：2096-4706（2020）24-0001-06

Parameter Derivation and Fault Detection of ARFA Model Based on VBEM

LI Jijun，ZHANG Zhijie，LI Qicao，DONG Zijian

（School of Electronic Engineering，Jiangsu Ocean University，Lianyungang  222005，China）

Abstract：In this paper，the autoregressive factor analysis（ARFA）model is used to model the dynamic process of data samples，and the methods of Kalman filter and EM algorithm to estimate the regression matrix parameter A and load matrix parameter C in ARFA model are analyzed. On this basis，a fault detection method based on variational Bayes EM（VBEM）is proposed to infer ARFA model parameters A and C and detect dynamic process faults. The simulation results show that under ARFA model，the detection effect of VBEM method is better than that of EM method for four kinds of faults，such as step signal and slope signal，and the average number of iterations is reduced.

Keywords：autoregressive factor analysis model;EM algorithm;variational Bayes EM;fault detection

0  引  言

随着科学和技术的发展，在信息化、数据化的今天，工业系统已逐渐呈现出大规模、强复杂性、高集成化等特点，对生产过程的安全、平稳、产品质量等提出了更高的要求。一旦复杂工程系统发生故障而又未能得到有效处理，不仅可能导致财产损失或人员伤亡，还可能导致环境污染造成生态灾难[1]。因此，常常采用有效的工业过程故障检测与诊断技术，来提高复杂工业过程控制系统的可靠性和安全性，及时有效地发现和检测出系统中存在的故障，以此来避免由故障造成的人员伤亡和经济损失[2]。传统的主元分析方法（Principal Com-ponent Analysis，PCA）是一种广泛应用于过程监控的线性方法，通过将原始高维空间的数据投影到低维空间中来消除数据间的相关性。然而在实际工业过程短采样中，还存在着数据的自相关性[3]。为解决这一问题，很多学者提出了多变量动态过程建模和故障检测的方法。KU[4]等人在1995年提出动态PCA（DPCA）算法，该方法通过把当前样本的前L个样本加入到数据矩阵中，构成时间滞后的数据增广矩阵，来提取时序相关的关系，从而消除数据的自相关性。LI[5]等提出了一种间接DPCA模型用于动态过程监测，该方法可以有效提取数据的自相关性，却忽略了数据的静态特性。

KIM[6]等提出了一种基于概率主成分分析（PPCA）的多变量过程监控方法。并指出当概率生成模型应用于过程监控时，大多数的统计量如单变量Shewhart图、多变量Shewhart图、T2和SPE统计量都可以被统一到概率模型的框架中。杨沛武[7]等提出了一种基于动态PPCA（Dynamic PPCA）的故障检测技术，通过增广时间序列变量来扩大数据矩阵，进而将数据的自相关性纳入相应的增广矩阵中来进行DPPCA建模。然而该方法无法全部获取数据的互相关特征。LI[8]等提出了一种新的动态隐变量模型（DLV）。在DLV中，采用AR模型创建了一个新的残差，并通过PCA分解来提取剩余部分的静态变化。而  和  统计量则分别用来监测动态和静态变化。因此，DLV能够同时提取数据的自相关性和互相关性。WEN[9]等提出了一种基于线性高斯状态空间模型（LGSSM）的动态过程监测方法。LGSSM通过一阶马尔科夫特性来描述过程的动态关系，并对过程数据做了降维处理。虽然该方法也能够同时提取数据的自相关性和互相关性，但对高阶动态过程的特征提取能力较差。周乐[10]提出了一种自回归因子分析模型（ARFA），它具有普适性的动态模型，能够同时提取数据间的动态和静态关系，有效提髙动态过程建模和故障检测效果。

本文在ARFA的等价模型和卡尔曼滤波的基础上，提出了一种新的变分贝叶斯EM的动态过程故障检测方法。该方法推导模型回归矩阵参数A和载荷矩阵参数C的期望和故障检测的总体思路是：由参数和数据的联合分布，根据变分理论求出A和C的边缘分布，再求出参数A和C的后验期望，并把这两个参数期望代入到ARFA的标准化模型和卡尔曼滤波方程中进行迭代，直到模型参数A和C收敛为止。把收敛后的模型参数代入T2和SPE统计量的相关公式中进行计算。当样本的两个统计量均在控制限以下时，则认为没有故障发生;均在控制限以上时，则认为有故障发生[3]。

本文安排为，第一节介绍ARFA模型及其EM算法;第二節为利用变分贝叶斯EM方法对ARFA模型进行推断;第三节为仿真实验;第四节为结论。

1  ARFA模型及其EM算法

1.1  ARFA模型及其等价系统

ARFA模型形式为：

fk=Azk-1+wk

jk=Cfk+vk                                   （1）

其中jk∈RM为测量变量，fk∈RD为动态因子，zk-1= [fk-1T，fk-2T，…，fk-LT]T∈RDL包含了动态因子的前L个值。A∈RD×DL为回归矩阵，C∈RM×D为载荷矩阵。系统的动态噪声和测量噪声分别为wk和vk，它们分别服从均值为零，方差为Q和R的高斯分布[10]。综上所述，ARFA的模型有效的参数为{A，C，Q，R}。

为了利用卡尔曼滤波来估计系统状态，ARFA模型可以等价为下述线性系统[10]：

（2）

系统（2）的定义与ARFA相似，因此，我们可以得到两者之间的关系为和  。相应的动态噪声，其中，

1.2  利用EM算法来估计ARFA模型参数A和C

K个输出序列J=（j1，j2，…，jk）T和它们相应的动态因子F=（f1，f2，…，fk）T的联合对数似然函数为：

（3）

在M步中，利用对数极大似然函数分别对A和C求一阶偏导数，得到的模型参数更新值为：

（4）

（5）

其中，矩阵、和  分别由式（6）、式（7）、式（8）给出：

（6）

（7）

（8）

1.3  基于ARFA模型的动态过程故障检测

我们构建T2和SPE两种统计量来检测动态过程是否发生故障。与传统的PCA构建T2统计量的方法不同，ARFA中动态因子fk由于包含了数据的动态关系而不再相互独立，因此，fk已经不再适用于直接构建统计量以检测隐变量空间的变化[10]。为此，我们利用动态因子的估计残差来构建T2统计量为：

（9）

（10）

其中， 由式（10）给出：

（11）

此外，根据模型的预测误差，我们可以构造SPE统计量为[10]：

（12）

SPE=ejkTejk                                （13）

根据正常样本的统计量，我们可以估计故障检测的统计限。T2统计量的控制限可以由χ2分布估计为[11]：

T2=T2lim=χ2（D）                        （14）

其中，α为显著性水平，D为动态因子的维度。

SPE统计量的控制限同样由近似的χ2分布估计为[12]：

SPE=SPElim～g·χ2（h）                 （15）

g和h满足以下方程，其中，α为显著性水平，g为常数，h为自由度。

gh=mean（SPEnormal）                   （16）

2g2h=var（SPEnormal）                   （17）

2  利用变分贝叶斯EM方法对ARFA模型进行推断

参数和数据的联合分布为：

P（A，C，fk，jk）=P（jk|A，C，fk）·P（A，C，fk）（18）

变分近似推导的目的就是为了寻找一个可以逼近待求后验分布、可以处理的函数。根据变分理论[13，14]有：

P（A，C，fk）≈q（A，C，fk）=q（A）q（C）q（fk）（19）

A的边缘分布为[15]：

（20）

其中，a（j）为A矩阵的第j列， 为协方差矩阵，SA，（j）为数量矩阵SA的第j列。

C的边缘分布为[15]：

（21）

其中，c（j）为C矩阵的第j列， 为协方差矩阵，SC，（j）为数量矩阵SC的第j列。

假定A和C矩阵中的超参数α和γ均如服从以下形式的伽马分布：

（22）

（23）

相关数据统计矩阵的表达式由式（24）、式（25）、式（26）、式（27）给出：

（24）

（25）

（26）

（27）

定义和的逆矩阵由式（28）和式（29）给出[15]：

（28）

（29）

qθ（θ）关于参数向量θ=（A，C）的变分后验的期望由式（30）和式（31）给出：

（30）

（31）

3  仿真实验

本文在处理器为CPU Intel i5-5200U 2.20 GHz的笔记本中，采用Matlab（2016b版本）编程语言来对一个二阶动态系统的数值例子进行仿真实验。数值例子为：

mk=Azk-1+wk

nk=Cmk+vk

其中，nk∈R4为k时刻的观测值，mk∈R2是其相应的动态因子，zk-1=[mk-1T，mk-2T]T∈R4包含了动态因子的前两个值。系统的动态噪声和测量噪声分别为wk和vk，它们均服从均值为0，方差为0.01的高斯分布。回归矩阵和载荷矩阵分别为：

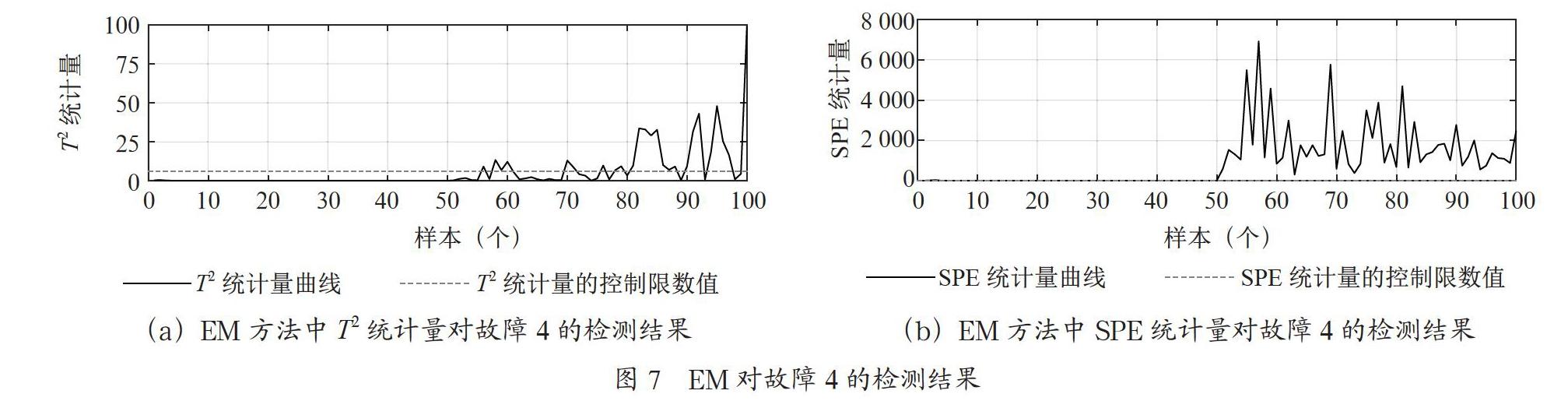
我们从标准正态分布中随机取出100个2维数据作为正常样本。为了进行故障检测实验，我们产生了四种测试集，每个测试集当中仍然包括100个样本点。这些测试集分别引入了四种不同的常见故障，它们分别是：故障1：在第51～100个样本点上引入幅度为8的阶跃信号故障;故障2：在第51～100个样本点上引入幅度为1.6×（50-t）的斜坡信号故障;故障3：在第51～100个样本点上引入幅度为0.48×（50-t）2的抛物信号故障;故障4：在第51～100个样本点上引入均值为12，方差为4的高斯噪声。

为了验证本文所提方法的有效性，我们在每种方法下对各种故障分别重复3 000次实验。并记录每次实验中T2统计量和SPE统计量的检测正确率以及所用方法的迭代次数，最后再把少部分的异常数据剔除掉并求取剩余数据在两种方法下的均值和方差，统计结果如表1所示。

由表1可以看出，EM方法中的T2统计量对故障1检测正确率的均值为0.277 3，而在VBEM方法中的均值为0.284 6。两种方法下的SPE统计量对故障1检测正确率的均值几乎相等。VBEM中的T2统计量和SPE统计量对故障2、3、4检测正确率的均值均高于EM方法。另外，从最后一列的平均值中也可以看到VBEM中的T2统计量和SPE统计量對总的故障检测正确率的均值也均高于EM方法。所用VBEM方法的平均迭代次数为4.061 8低于EM方法的平均迭代次数4.666 2。总的来说，VBEM方法对本文所述四类故障的检测效果要优于EM方法。

如图1～8所示为在某次实验中所得到的两种方法对各故障的检测结果。图中水平虚线为正常数据下的统计量的控制限，实线曲线分别为数据的T2统计量和SPE统计量，当统计量超过它们的控制限时，则表明检测到系统有故障发生。

如表2所示，在EM方法中T2统计量的漏报率较为严重。在VBEM方法中图2和图8的T2统计量的漏报率也较为严重。在EM方法中SPE统计量的漏报率较小。在图3中SPE统计量的漏报率仅为2%。在图5中SPE统计量的漏报率仅为14%。在VBEM方法中SPE统计量的检测正确率为100%，漏报率为0%。

4  结  论

本文针对ARFA模型下的动态过程故障检测问题，构建了相应的T2和SPE两种统计量，并提出了一种新的变分贝叶斯EM故障检测方法。在对上文所述四类故障的正确检测率上，本方法要优于传统的EM故障检测方法。但本文未对高阶动态系统和实际的工业数据进行仿真实验，因此这也是今后的一个研究方向。

参考文献：

[1] 何潇，郭亚琦，张召，等.动态系统的主动故障诊断技术 [J].自动化学报，2020，46（8）：1557-1570.

[2] 王世林.基于多元统计分析的工业过程故障检测研究 [D].北京：华北电力大学（北京），2018.

[3] 刘春燕.基于PCA的过程工业故障检测 [D].绵阳：西南科技大学，2017.

[4] KU W，STORER R H，GEORGAKIS C. Disturbance detection and isolation by dynamic principal component analysis [J].Chemometrics and Intelligent Laboratory Systems，1995，30（1）：179-196.

[5] LI W H，QIN S J. Consistent dynamic PCA based on errors-in-variables subspace identification [J].Journal of Process Control，2001，11（6）：661-678.

[6] KIM D，LEE I B. Process monitoring based on probabilistic PCA [J].Chemometrics and Intelligent Laboratory Systems，2003，67（2）：109-123.

[7] 杨沛武.概率PCA多元统计方法在过程监控中的应用研究 [D].无锡：江南大学，2008.

[8] LI G，QIN S J，ZHOU D H. A New Method of Dynamic Latent-Variable Modeling for Process Monitoring [J].IEEE Transactions on Industrial Electronics，2014，61（11）：6438-6445.

[9] WEN Q J，GE Z Q，SONG Z H. Data-based linear Gaussian state-space model for dynamic process monitoring [J].AlChE Journal，2012，58（12）：3763-3776.

[10] 周乐.基于概率的工业过程数据建模与故障检测 [D].杭州：浙江大学，2015.

[11] QIN J S. Statistical Process Monitoring：Basics and Beyond [J].Journal of Chemometrics，2003，17（8-9）：480-502.

[12] BOX G E P. Some Theorems on Quadratic Forms Applied in the Study of Analysis of Variance Problems，I. Effect of Inequality of Variance in the One-Way Clas-sification [J].The Annals of Mathematical Statistics，1954，25（2）：290-302.

[13] JAAKKOLA T S. Tutorial on variational approximation methods [M]//OPPER M，SAAD D. Advanced Mean Field Methods：Theory and Practice.Massachusetts：MIT Press，2001：129-159.

[14] JORDAN M I，GHAHRAMANI Z，JAAKKOLA T S，et al. An Introduction to Variational Methods for Graphical Models [J].Machine Learning，1999，37（2）：183-233.

[15] BEAL M J. Variational algorithms for approximate Bayesian inference [D].London：University College London，2003.

作者簡介：李吉俊（1995—），男，汉族，河南邓州人，硕士研究生在读，研究方向：故障检测、图像处理;章智杰（1996—），男，汉族，江苏连云港人，硕士研究生在读，研究方向：图像处

理;李其操（1997—），男，汉族，浙江诸暨人，硕士研究生在读，研究方向：图像处理;通讯作者：董自健（1973—），男，汉族，江苏连云港人，教授，博士研究生，研究方向：检测与控制、通信技术。