基于贝叶斯分类器的多普勒天气雷达海浪回波识别和效果检验

沈妍琰, 黄兴友, 黄书荣, 沈艳秋, 陈晓颖

基于贝叶斯分类器的多普勒天气雷达海浪回波识别和效果检验

沈妍琰, 黄兴友, 黄书荣, 沈艳秋, 陈晓颖

(南京信息工程大学 大气物理学院, 江苏 南京 210044)

为了提升雷达数据质量, 减少海浪回波对临近预报和数值天气预报模式的雷达数据同化的不利影响, 因此需要对海浪回波进行识别和去除。识别算法主要为统计获得先验概率, 分析海浪和降水回波特征分布得到似然函数, 再经过贝叶斯分类器来达到识别的目的。在本次算法识别过程中65个样本数据试验的临界成功指数CS达到了0.692, 结果表明利用贝叶斯分类器对海浪回波的识别, 具有较好的识别效果, 能一定程度降低海浪回波误判为降水回波的错误, 提高雷达数据质量。

海浪回波; 回波识别; 贝叶斯分类器; 似然函数; 先验概率

沿海地区的雷达回波上经常会出现海浪回波, 这一类非气象回波主要是由超折射现象引起的, 在一定程度上影响了雷达资料质量, 同时对降水回波产生干扰。海浪回波主要出现在海面区域, 由许多针状的回波体组成, 呈扇形向外辐散, 回波高度比较低, 一般出现在雷达探测仰角为0.5°的回波中, 很少出现在第二个探测仰角中。海浪回波的径向速度偏小, 主要集中在–10~5 m/s, 和降水回波相比, 在回波形态, 垂直结构, 径向速度等方面有较大的差异。

随着高分辨率数值天气预报(NWP)的快速发展, 在NWP中对雷达数据进行同化(DA, Data assimilation)是十分有必要的。为了向数值模式提供可靠的雷达数据, 首先需要对雷达数据进行质量控制, 判别降水回波和非降水回波。沿海地区雷达探测的海浪回波是一种典型的常见非降水回波, 需要被识别和去除。国内外科研人员在这方面做了很多研究, 同时也形成了多种杂波识别方法。Kessigner等[1]采用模糊逻辑方法, 在识别地物, 晴空等非降水回波方面有明显效果, 该识别方法已经广泛运用于美国的天气雷达系统。Lakshmanman等[2]采用神经网络对雷达数据进行质量控。国内刘黎平等[3]提出分步式的模糊逻辑方法对超折射地物回波进行识别, 取得了一定的识别效果。谭学等[4-5]采用类似于超折射地物杂波的识别方法、对海浪回波进行了回波特征的分析, 利用回波分块和基于模糊逻辑的分布式海浪回波识别方法对福州、温州的SA型雷达数据进行了有效的海浪回波识别。为了能提高回波分类识别的可靠性, 统计分析领域的贝叶斯分类理论被运用到回波分类识别并取得了一定的进展。Nicol等[6]利用贝叶斯分类器技术提高了对地物杂波识别的效果, Peter等[7]采用贝叶斯分类器(NBC)识别超折射传播(AP)海浪杂波和降水回波, 使用的特征量包括回波顶部高度、垂直梯度和纹理。

目前国内研究大多使用模糊逻辑算法和机器学习分类算法进行海浪与降水回波的识别。模糊逻辑依赖于通过大量实践得到的模糊控制规则, 不需要精确的数学模型, 但缺乏整体设计的系统性; 传统的机器学习分类算法, 大多需要大批量的数据集训练, 会耗费大量的计算时间和存储空间资源。本文利用海浪和降水回波的类条件概率对海面区域的回波先验概率进行修正得到最终的海浪回波概率, 识别过程的计算较为简单, 通过对识别结果的分析, 可以确认贝叶斯分类器识别海浪回波的效果较好。

1 贝叶斯分类器及其原理

贝叶斯分类器分为朴素贝叶斯分类器和半朴素贝叶斯分类器, 两者的主要区别在于分类变量是否互相独立[8-9]。本文利用的贝叶斯分类器为半朴素贝叶斯分类器中的TAN(Tree Augmented native Bayes) , 是由Friedman 等人提出的一种树状贝叶斯网络, 是朴素贝叶斯分类器的一种改进模型, 使用的变量并不完全相互独立, 依然存在一些联系, 这类贝叶斯分类器的理论基础为最大带权生成树。

贝叶斯分类器是各种分类器中分类错误概率最小或者在预先给定代价的情况下平均风险最小的分类器, 其分类原理是通过某对象的先验概率, 利用贝叶斯公式计算出其后验概率, 即该对象属于某一类的概率, 选择具有最大后验概率的类作为该对象所属的类。

在利用贝叶斯理论进行海浪回波和降水回波的二分类识别时, 贝叶斯公式可以改写为:

其中,()是由贝叶斯分类器最终得到的该回波点出现海浪回波的概率;()()分别代表了回波点出现海浪回波和降水回波的预期概率, 也即贝叶斯理论中的先验概率, 在二分类问题中假设出现海浪回波和降水回波的概率和为1, 即()()1,若()=()=0.5, 即我们认为在任何时候出现海浪回波和降水回波的概率都是一样的, 则此时的贝叶斯分类器称为朴素贝叶斯分类器, 但实际情况中, 不同季节不同天气条件下海浪回波的出现概率并不是0.5, 因此需要对大量的数据进行统计。

而在整个贝叶斯分类过程中, 识别的准确性主要取决于海浪回波()和降水回波()这两类类条件概率, 通过贝叶斯公式对先验概率进行修正, 得到的()也称为后验概率即最终判定的海浪回波的概率(POC, Probability of Clutter)。

2 研究数据及识别区域

2.1 雷达数据预处理

文中使用的数据来自于广东省汕头市的SA型多普勒天气雷达, 雷达站位置为(116°4159E, 23°1750N), 由于雷达处于海岸线附近, 因此, 该雷达容易接收到海浪回波。输出数据包括径向分辨率为1 km的反射率因子()、250 m的径向速度()以及250 m的谱宽()。雷达采用体扫模式VCP21(降水模式)进行探测。为了减少噪声影响, 对径向速度数据进行了中值滤波处理。

由于雷达强度数据以及速度和谱宽数据在不同探测仰角下的径向库数目以及分辨率不同, 在计算特征量之前采用刘黎平等[3]提出的方法, 将雷达数据进行径向处理, 按照严格的1°间隔顺次排列径向数据, 以满足同一回波点回波强度, 径向速度和谱宽数据的一一对应。

2.2 识别海面区域

算法中采用贝叶斯分类器来处理海浪回波和降水回波的二分类问题, 为了尽量减少地物回波以及晴空回波对算法识别效果的影响, 仅对雷达探测范围内的海面区域进行算法识别, 即位于雷达东北方向顺时针至雷达西南方向的有效探测区域。

3 海浪回波识别方法

为了利用贝叶斯分类器进行降水回波和海浪回波的分类识别, 首先对汕头雷达近三年的回波数据进行统计, 得到各个格点出现回波的频率即先验概率, 然后分析得到的海浪回波和降水回波的类条件概率()()再通过贝叶斯公式(1)与先验概率进行修正得到海浪回波的概率, 最后通过阈值判断每个格点是否为海浪回波。

3.1 先验概率

先验概率就是事件发生的预先估计概率。本文利用广东汕头SA雷达在2010—2012年探测的233 380个体扫数据, 统计得到了汕头SA雷达仰角为0.5°区域格点出现回波的概率图(见图1)。

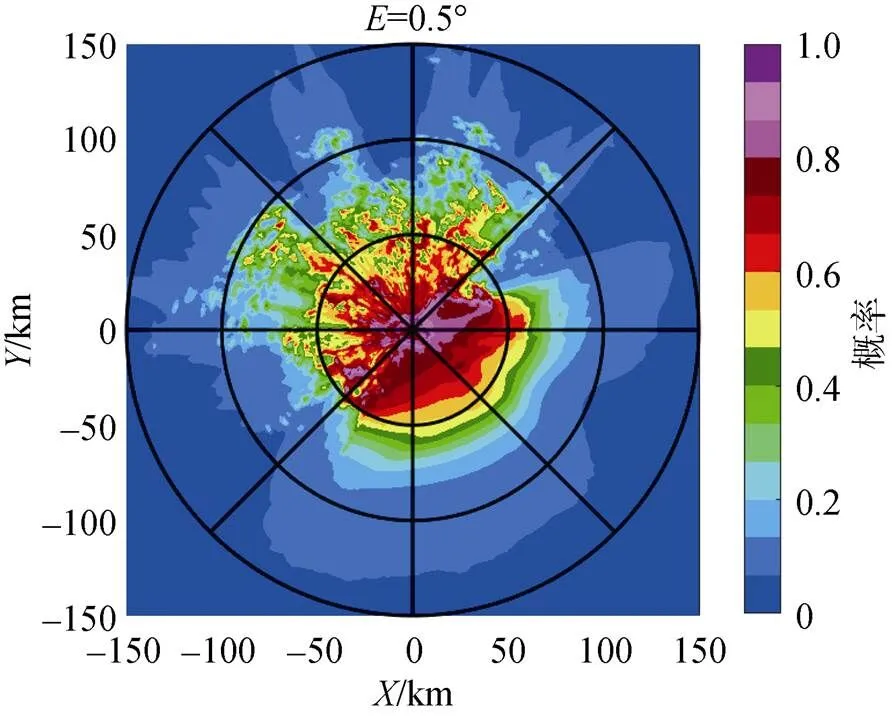
图1 2010—2012年汕头SA雷达0.5°仰角的回波概率图

从汕头SA雷达3年的区域格点回波概率可以看出, 在雷达东北至西南近距离圈内高频出现的有晴空回波, 超折射地物回波以及海浪回波, 而稍远距离的海面上回波概率仅为0.3以下, 符合沿海雷达的回波分布特征。可以看出海面区域海浪回波的出现概率并不能简单假设为50%, 通过统计获得的先验概率体现出了贝叶斯分类器在分类识别方面的优势, 进而提高回波识别的准确率。

3.2 特征参量选取

通过分析海浪回波和降水回波差异, 选用4个物理量用于识别海浪回波, 它们是: 回波强度()垂直变化GDBZ和纹理TDBZ; 径向速度的区域平均值MDVE; 速度谱宽的区域平均值MDSW。这4个参量的计算公式分别为:

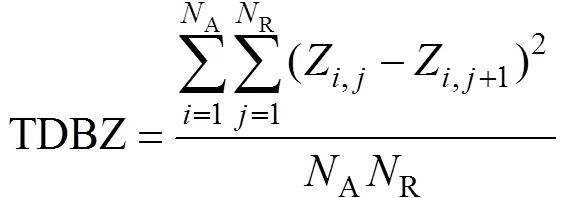
式中，A,R分别代表了在方位和径向距离方向上定义的计算区域大小,和分别表示距离以及方位角的索引;low和up代表了本层和上层的回波强度,low和up为本层和上层的回波仰角的度数, GDBZ反映了回波强度的垂直变化。由于海浪回波很少出现在第二层, 因此当出现库上无回波数据时, 为了计算方便, 将缺省值设置为–33(远低于正常回波的强度); TDBZ反映了回波强度的局地变化, 回波越均匀, TDBZ越小, 反之越大。对于天气雷达的探测参数, 目前普遍认为7×7与9×9的区域都能较好地体现回波的纹理特征, 因此, 本文识别中选取9×9为TDBZ的计算范围; 而MDVE和MDSW的计算区域选取最小的范围3×3即可。

3.3 似然函数

分别选用汕头SA雷达的纯降水回波数据和纯海浪回波数据进行统计, 其中降水数据包括层状云降水, 对流型降水, 混合型降水过程。通过对降水和海浪数据的统计分析, 得到海浪回波和降水回波的GDBZ, TDBZ, MDVE和MDSW的概率分布(图2)。可以看出, 海浪回波的径向速度都偏负数、速度值较小; 海浪回波的TDBZ较降水回波的大, 说明海浪回波的分布没有降水回波的均匀; 并且海浪回波的垂直梯度GDBZ明显大于降水回波, 因为海浪回波通常只出现在0.5度仰角, 高仰角中不出现。

图2 海浪和降水回波的四个特征参量 TDBZ, GDBZ, MDVE以及MDSW概率分布图

根据各个参量的概率密度分布, 采用YO-HAN CHO等人[10]通过概率分布确立似然函数的计算方法, 分析统计得到的海浪回波和降水回波特征参量的概率分布特征, 最终选择梯形折线来表示此次研究算法中海浪回波特征参量的似然函数, 函数值均为0~1区间(图3)。

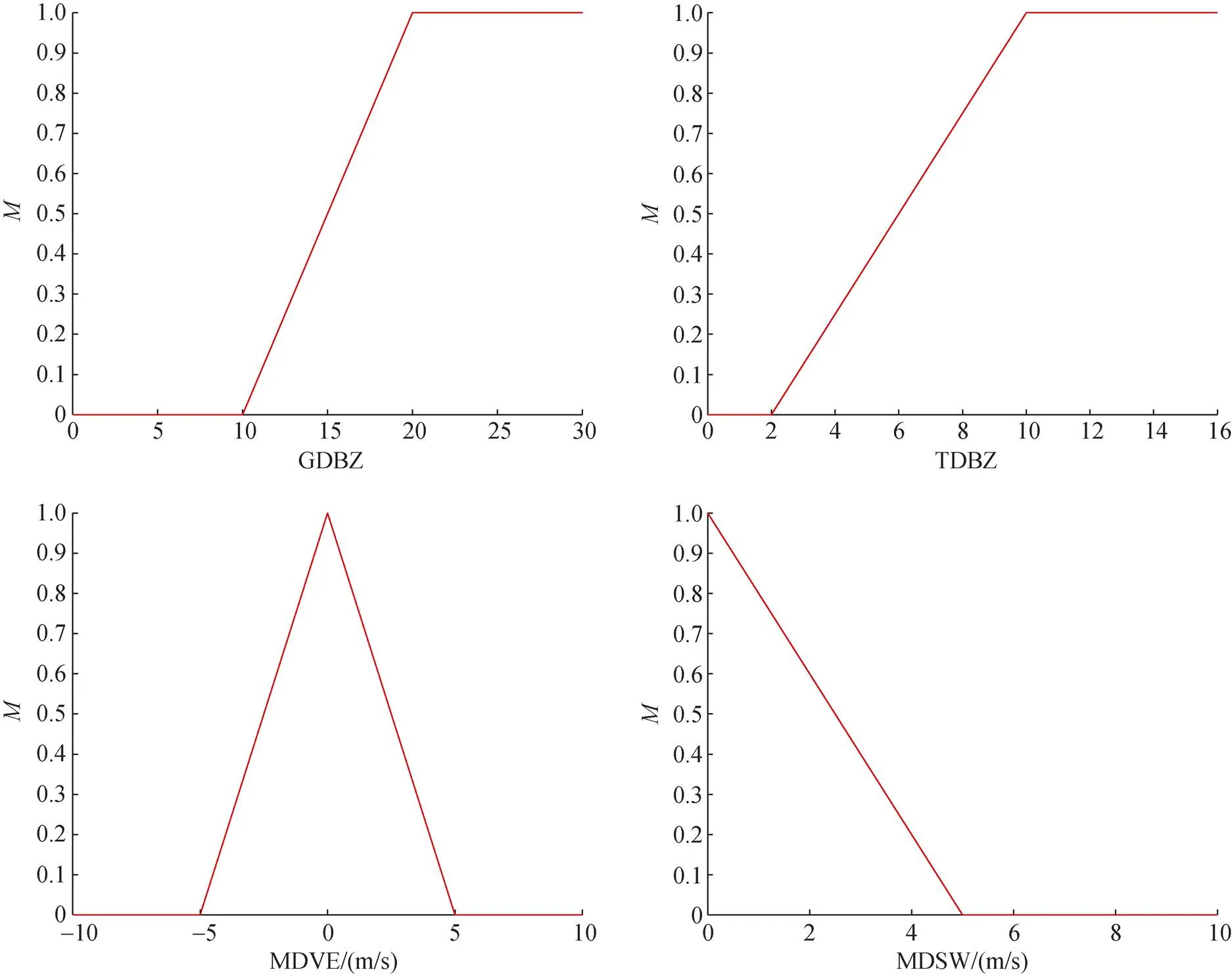
图3 贝叶斯分类器中四个物理量 TDBZ, GDBZ, MDVE以及MDSW的似然函数

3.4 逐点识别

对于雷达基数据中的各个回波点计算其特征量, 并通过对应特征量的似然函数, 计算各自的判据值, 然后对每个点进行加权求和, 具体计算公式为:

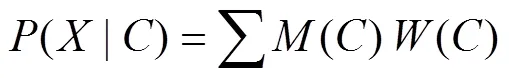
其中()为贝叶斯分类器中海浪回波的类条件概率,()为通过似然函数得到的各个特征参数的函数值,()为各个特征参量的权重系数(如表1)。由于研究的是二分类问题,()()=1, 因此()的数值越大, 则代表了()越小, 回波点为海浪回波的可能性越大, 反之, 是降水回波的可能性就越大。之后再将得到的(),()代入贝叶斯分类公式(1)中计算最后的(), 即该回波点出现海浪回波的最终概率, 再通过阈值判断来进行逐点识别。

表1 特征量及其权重系数

3.5 算法流程图

具体算法步骤见图4。

图4 算法流程图

4 识别效果

为了检验识别效果, 选取了不同天气条件下的两个海浪回波个例, 分别为台风降水(图5)、层状云降水(图6), 检验贝叶斯分类器对海浪回波的识别效果。

4.1 台风降水

2010年8月29日 06时(世界时, 下同)汕头雷达观测到的一次超折射海浪回波, 当仰角为0.5°时,在雷达东南侧距离雷达站0~50 km的海面区域上存在一块弱的回波体, 回波较弱, 很难达到1.5°仰角体扫, 径向速度与降水回波相比较小, 可以判断出该回波为海浪回波, 利用贝叶斯分类器可以较准确地识别海浪回波, 并对海浪回波进行了滤除, 提高雷达的降水回波数据质量。

4.2 层状云降水

2010年1月7日13时30分, 汕头雷达观测到的一次海浪回波。从图6中可以看出, 雷达站周围出现了大面积的层状云降水回波, 在海面区域0.5°仰角的强度PPI回波图上也出现了明显的扇形海浪回波, 将仰角抬高至1.5°后, 该回波形态基本消失, 从0.5°和1.5°仰角的径向速度上可以看出, 海浪回波的径向速度比降水回波要小。由于降水回波的面积较大, 在一定程度上与海面的海浪回波有了重叠, 这对海浪回波的识别造成了一定的困难。

第五幅图为利用贝叶斯分类器识别和滤除海浪回波后的0.5°仰角反射率因子, 距离雷达站50 km内的海浪回波基本被滤除, 但仍然保留了一些弱的、没有被正确识别的海浪回波点, 这些“杂点”的回波强度为0左右, 远低于正常降水回波强度, 不会对降水回波数据质量产生显著影响。可以看出, 当雷达站附近出现大范围降水回波并与海浪回波存在重叠的情况下, 利用贝叶斯分类器可以对海浪回波进行有效的识别。对海浪回波被剔除后所产生的回波“空洞”, 可以利用第二层仰角的数据进行插值填补, 使得降水回波更具连续性, 最终得到填补后的0.5°仰角的雷达反射率因子PPI图像。

5 识别效果评估

选取广东汕头SA雷达探测到的65个存在海浪回波的体扫数据进行算法效果检验, 其中贝叶斯分类器成功识别出海浪回波的样本数为45个, 未能识别的为20个, 误识别的为0个。针对检验结果, 采用临界成功指数来进行效果评估, 具体指标为临界成功指数CS, 命中率H, 漏报率M以及虚警率FA, 计算公式如下:

公式(7)中x为成功识别样本数, y为未能识别但实际存在的海浪回波样本数, z为无海浪回波但将降水回波误识别为海浪回波的样本数。本次试验中, ICS为0.692, RH为0.692, RM为0.308, RFA为0。临界成功指数达到0.692显示贝叶斯分类器对于海浪回波的识别效果较好, 但为了能够更准确的识别海浪回波, 还需进一步的研究。

6 结论

利用广东汕头SA雷达观测数据, 分析了海浪回波和降水回波的回波特征, 主要利用了回波强度, 径向速度和速度谱宽资料, 借助贝叶斯分类器, 对海浪回波进行了识别和去除, 研究表明:

1) 降水回波和海浪回波的垂直变化(GDBZ)、回波强度的纹理(TDBZ)、径向速度区域平均值(MDVE)和速度谱宽区域平均值(MDSW)有明显的区别, 可以作为识别和去除海浪回波的主要特征量。

2) 利用贝叶斯分类器, 能够较为有效地区分海浪和降水回波, 通过调整先验概率和似然函数, 本文的研究方法同样可用于其他沿海地区雷达的海浪回波识别。贝叶斯分类器具有稳定的海浪回波识别效果, 体现了贝叶斯分类器在海浪回波识别领域的价值。

3) 雷达站周围长期存在着很弱的晴空回波, 利用贝叶斯分类器进行海浪回波识别滤除的同时, 由于缺少准确的海面区域地理数据, 可能会将部分晴空回波剔除。

4) 贝叶斯分类器的准确性和稳定性主要依赖于统计得到的先验概率以及似然函数, 因此需要对大量的样本数据进行统计, 以便提高贝叶斯分类器的识别效率。

[1] Kessiner C, Ellis S, Vanandel J, et al. The AP clutter mitigation scheme for the WSR-88D[C]//Amer Meteor Soc. Preprints of 31st Conference on Radar Meteorology, Seattle Washington. Washington: Amer Meteor Soc, 2003: 526-529.

[2] Lakshmanan V, Hondl K, Stumpf G, el al. Quality control of weather radar data using texture features and a neural network[C]//IEEE. Proceedings of the 5th International Conference on Advances in Pattern Recognion. Kolkata: IEEE: 2003: 15-18.

[3] 刘黎平, 吴林林, 杨引明.基于模糊逻辑的分步式超折射地物回波识别方法的建立和效果分析[J]. 气象学报, 2007, 65(2): 252-260. Liu Liping, Wu Lingling, Yang Yinming. Development of fuzzy-logical two-step ground clutter detection algorithm[J]. Acta Meteorologica Sinica, 2007, 65(2): 252- 260.

[4] 谭学, 刘黎平, 范思睿. 新一代天气雷达海浪回波特征分析和识别方法[J]. 气象学报, 2013, 71(5): 962- 975. Tan Xue, Liu Liping, Fan Sirui. Statistical characteristics of sea clutter and its identification with the CINRAD. Acta Meteorologica Sinica, 2013, 71(5): 962-975.

[5] 谭学, 刘黎平, 范思睿. 福州SA雷达新观测模式结果对比及海浪回波识别[J]. 成都信息工程学院学报, 2013, 28(5): 513-519. Tan Xue, Liu Liping, Fan Sirui. Comparison of detecting result using new volume scan strategies and identification of sea clutter with Fuzhou SA Radar[J]. Journal of Chengdu University of Information Technology, 2013, 28(5): 513-519.

[6] Hubbert J C, Dixon M, Ellis S M. 2009: Weather radar ground clutter. Part II: Real-time identification and filtering[J]. Atmos Oceanic Technol, 2009, 26: 1181-1197.

[7] Peter J R, Seed A, Steinle P. Application of a Bayesian classifier of anomalous propagation to single-polariza­tion radar reflectivity data[J]. Atmos Oceanic Technol, 2013, 30: 1985-2005.

[8] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 第三版. 北京: 高等教育出版社, 2001: 22-26. Sheng Zhou, Xie Shiqian, Pan Chengyi. Probability theory and mathematical statistics[M]. The Third Edition. Beijing: Higher Education Press, 2001: 22-26.

[9] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 147-164. Zhou Zhihua. Machine Learning[M]. Beijing: Tsinghua University Press, 2016: 147-164.

[10] Cho Y H, Lee G W, Kim K E, et al. Identification and removal of ground echoes and anomalous propagation using the characteristics of radar echoes[J]. Journal of Atmospheric and Oceanic Technology, 2006, 23(9): 1206-1222.

Identification and validation of sea-wave echoes collected by a Doppler weather radar based on a Bayes classifier

SHEN Yan-yan, HUANG Xing-you, HUANG Shu-rong, SHEN Yan-qiu, CHEN Xiao-ying

(Nanjing University of Information Science and Technology, Nanjing 210044, China)

Weather radar data quality is usually degraded due to the presence of sea-wave echoes in coastal areas. To deduce problems caused by non-precipitation sea-wave echoes in nowcasting and numerical weather models while assimilating radar measurements, sea-wave echoes need to be identified and removed. The key of a Bayes classifier for the classification of precipitation and sea-wave echoes is the prior probability and likelihood function based on statistics. An experiment with 65 samples shows that the Critical Successful Indexcsis 0.692, which implies that the Bayes classifier works well in identifying sea-wave echoes. The classification of sea-wave echoes with the Bayes classifier can also mitigate the chance of being regarded as precipitation echoes.

sea-wave echo; echo identification; Bayes classifier; likelihood function; prior probability

Oct. 11, 2019

P406

A

1000-3096(2020)06-0083-08

10.11759/hykx20191011001

2019-10-11;

2019-11-15

国家重点研发计划(2018YFC1506102)

[National Key R&D Program of China, No.2018YFC1506102]

沈妍琰(1995-), 女，江苏南通人, 硕士, 研究方向为雷暴天气中的灾害性天气识别, 电话: 13260816017, E-mail:425881170@qq.com; 黄兴友,通信作者, 主要从事雷达气象学, 雷达及其他遥感资料的处理和应用研究, E-mail: hxyradar@126.com

(本文编辑: 刘珊珊)