浅析两类光源下的菲涅耳圆孔衍射*
2020-06-28靳龙
靳 龙
(湖北汽车工业学院理学院,湖北 十堰 442002)
菲涅耳圆孔衍射实验不仅操作简单、现象直观,而且易于通过图解法来阐明,被广泛应用在高中物理、大学物理以及光学的教学素材中[1]。相较于夫琅禾费衍射,菲涅耳衍射属于近场衍射,故一般应在距离衍射屏比较近的菲涅耳区观察出射光波的这类衍射现象,而对入射光的位置和类型则没有限制[2-5]。随着激光器的发展和普及,在演示这类现象时,通常以高斯光束替代传统的自然光波作为入射光源;而在理论教学中,却以普通的球面光波或平面光波作为入射光源,利用菲涅耳半波带法和振幅矢量法进行相关理论教学。光源的差异是否会对接收屏上的菲涅耳衍射光强分布产生影响,进而导致理论和实验教学的不自洽,是专业教师在教学环节中需要探索的问题。
另外,在利用菲涅耳-基尔霍夫积分公式定量计算圆孔菲涅耳衍射时,会遇到非常繁琐的积分运算,通常只能利用数值积分近似计算,但垂直圆孔中心轴线上的衍射光强分布,却有解析解。故本文利用菲涅耳-基尔霍夫积分公式,研究了高斯光束和平面光波两种光源照射下,接收平面对应轴线上的菲涅耳衍射光强分布,探究了这两类衍射光波相对光强分布随传输距离和圆孔半径的变化规律,进一步分析了高斯光束束腰半径对衍射光强分布的影响。研究结果证实了理论和实验教学中使用不同种类光源进行菲涅耳衍射观测是可行的,同时相关结论和研究方法可以作为专业教师的教学参考。
1 两类光源下的菲涅耳圆孔衍射理论建模
当光波通过圆形孔径光阑,将在菲涅耳区发生次波叠加,对应接收屏上任一点的电场复振幅可通过菲涅耳-基尔霍夫积分公式描述[6]为

式中:E2(x,y,z)为出射光波电场强度;E1(x0,y0,0)为入射光波电场强度;∑为积分区域。因为求解区域在轴线上,故x=y=0,这样可以简化积分求解过程,所得结论又不失一般性。同时,考虑到是圆孔衍射,故需将直角坐标系变换为柱坐标系,这样,式(1)可以改写为
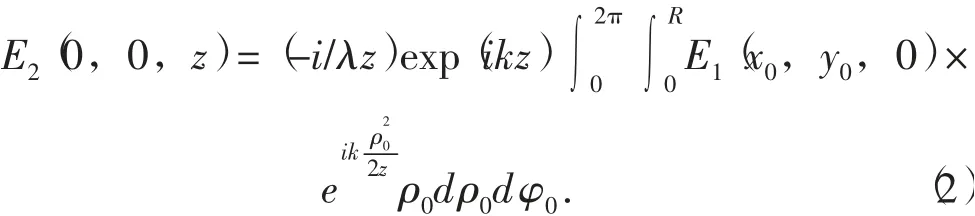
式中:R为圆孔半径。对于入射平面光波,其电场强度在忽略相位因子后可简单表示为
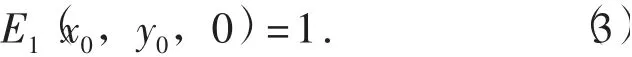
将式(3)代入式(2),便可求得观察屏中心处的菲涅耳电场强度分布为

如光源为高斯光束,则其电场强度分布[7]为

式中:ω0为高斯光束的束腰半径。利用式(5)和式(2),同理可以求出对应位置高斯光束的电场强度分布为

可以看出,当入射激光的束腰半径ω0→∞,高斯光束的菲涅耳衍射电场强度分布便与传统平面光波无异。一般情况下,观测屏轴线上相应光波的菲涅耳光强分布可由式(4)或式(6)及其复共轭求得,具体公式为
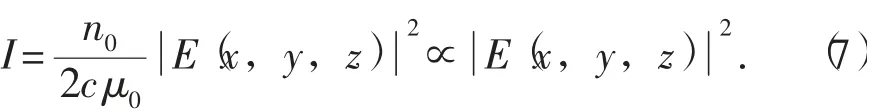
式中:c为真空中的光速;μ0为真空磁导率;n0为自由空间折射率。三者均为常量。
2 两类光源下的菲涅耳圆孔衍射实验结果与讨论
2.1 平面光波菲涅耳圆孔衍射光强分布特性
平面光波经过圆孔后,研究衍射光强随传输距离z的变化规律。图1 给出了轴线上不同位置处的归一化相对光强分布曲线,其中,入射光波长λ=632.8 nm,圆孔半径R=0.5 mm。从图1 可以看出,当时,菲涅耳衍射效应显著,且随着传输距离z 的增加,轴线上的光强发生着明暗交替的变化;而当后,光强将单调减小,表明衍射区域已逐渐进入远场夫琅禾费区。图2 给出了在z=0.395 m 处,相对光强随圆孔半径R的变化曲线。从图2 可以看出,随着圆孔半径的增加,相对光强逐渐增加,然后在时达到极大值,进而又继续减小。以上结论都与利用菲涅耳半波带法定性研究的结果一致[8],但利用菲涅耳-基尔霍夫积分公式求出了圆孔轴线上菲涅耳衍射光强的解析解,从而定量分析了轴线上相对光强的变化情况。
2.2 高斯光束菲涅耳圆孔衍射光强分布特性
研究高斯光束在轴线上的相对光强随传输距离z和圆孔半径R的变化规律,结果见图3 和图4,其中ω0=0.1 mm。从图3 可以看出,在菲涅耳衍射区域,高斯光束在轴线上的相对光强分布随传输距离的变化规律与传统平面光波分布规律基本一致,只是受束腰半径的影响,光强各极大值均有所减弱。分析图4 可知,当光波由理想平面光波变为激光束时,衍射光波随R的增加仍产生光强的强弱转换,只是此时光强的极大值出现在处,这表明在同一位置z处,要使得高斯光束和平面光波的明暗变化规律一致,高斯光束所使用的衍射圆孔半径应稍微小于平面光波所使用的圆孔半径。

图1 平面光波相对光强随传输距离的变化曲线

图2 平面光波相对光强随圆孔半径的变化曲线

图3 ω0=0.1 mm 时高斯光束相对光强随传输距离的变化曲线
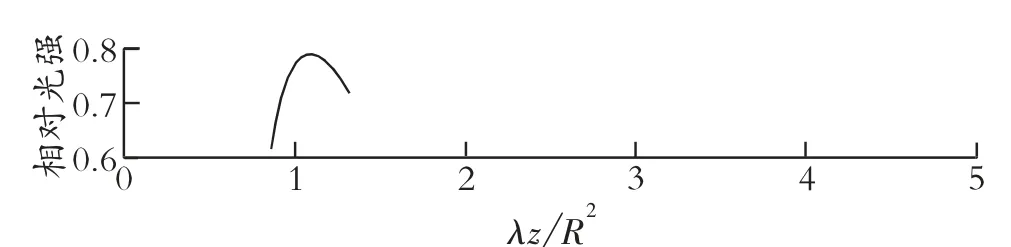
图4 ω0=0.1 mm 时高斯光束相对光强随圆孔半径的变化曲线
当高斯光束的束腰半径变化时,光波在轴线上的衍射光强分布也会随之发生变化。第68 页图5为ω0=0.5 mm 时高斯光束相对光强随传输距离的变化曲线;图6 为ω0=0.05 mm 时高斯光束相对光强随传输距离的变化曲线。从图5 可知当ω0=0.5 mm时,对应光波衍射光强分布和图1 差别很小;而从图6 可知,当ω0=0.05 mm 时,在菲涅耳衍射区内,光强虽然随传输距离有明暗交替变化,但与图5 相比,光强极大值迅速减弱,而极小值却相应增加,表明随着束腰半径的减小,高斯光束的菲涅耳衍射特性逐渐减弱。因此,在实验教学中,应尽量使用较大束腰半径的激光光源进行菲涅耳圆孔衍射实验,这样所观测到的菲涅耳圆孔衍射图样会和理论教学所得的结论高度吻合。

图5 ω0=0.5 mm 时高斯光束相对光强随传输距离的变化曲线
3 结束语

图6 ω0=0.05 mm时高斯光束相对光强随传输距离的变化曲线
利用菲涅耳-基尔霍夫积分公式,定量研究了高斯光束和平面光波通过圆形孔径光阑时,其轴线上菲涅耳衍射光强的分布规律。通过对比两类光波衍射的相对光强分布随传输距离和圆孔半径的变化曲线可以看出,高斯光束的菲涅耳圆孔衍射光强分布特性和传统平面光波的菲涅耳圆孔衍射光强分布特性以及演变规律基本相同,并且随着高斯光束束腰半径的增加,激光光源的菲涅耳圆孔衍射特性越来越接近传统平面光波的菲涅耳圆孔衍射特性。因此,在普通物理教学中,使用这两类光波分别进行菲涅耳圆孔衍射理论和实验教学是合适的,并且该研究方法数学积分简单、物理图像清晰,适宜作为普通物理教师的教学参考。
