f-k滤波在探地雷达数据去噪中的应用

吴海波，张平松，胡雄武，秦 镇

(1.中国矿业大学(北京)煤炭资源与安全开采国家重点实验室，北京 100083;2.安徽理工大学地球与环境学院，安徽 淮南 232001)

探地雷达作为一种新兴的工程物探手段，现广泛用于城市工程、水利以及交通工程检测中的多个环节，包括道路路基检测、地下管线探测、隧道超前探测与衬砌检测，以及土体、坝体检测等。但在探地雷达数据采集过程中，受到环境、人为以及仪器等因素制约，探地雷达数据不可避免的会受到噪声干扰。噪声的存在不仅限制了有效信号的精确识别，同时会产生“虚假”异常，对探地雷达的数据处理和解释工作造成严重的影响[1-3]。

目前，频域滤波是去除探地雷达数据中噪声干扰的有效方法[4]。带通滤波器、巴特沃斯滤波器等常被用于探地雷达数据的滤波处理[5]。除此之外，一些非线性的时频分析及变换方法，如小波阈值、经验模分解、主成分分析法-奇异值分解等也在探地雷达数据处理中得以应用[6-9]。但总体而言，现阶段多数滤波方法仍较多的关注单一频率因素，造成部分情况下滤波的效果不理想。为了克服单一因素滤波的局限性，部分学者尝试将地震数据勘探中的f-k滤波方法应用到探地雷达数据处理中来，但这部分研究更多的是关注直达波与有效回波的分解问题[10-12]。

为此，本文将重点聚焦于探地雷达数据中噪声的滤除，寻求通过分析含噪声正演记录与实采数据的f-k谱特征，并设计具有针对性的扇形滤波器，通过f-k滤波实现探地雷达数据中噪声的滤除，保留并突出被噪声“掩盖”的有效回波。

1 f-k滤波方法

1.1 二维傅里叶变换

f-k滤波的理论基础为二维傅里叶变换。设雷达信号为y(t，x)。t为时间变量，而x为空间变量，则y(t)表示单道记录；y(t，x)表示多道记录。定义y(t，x)的二维正反傅里叶变换分别为

(1)

式中：Y(f，k)称为y(t，x)的频率—波数谱(f-k谱)，相应的变换称为f-k变换。

通常采集的探地雷达数据为离散数据，则离散二维正反傅里叶变换可表示为

(2)

1.2 滤波器设计

f-k域的二维滤波方程表示为

(3)

式中：Y(f，k)可由二维傅氏变换得到，H(f，k)为设计的滤波器。

探地雷达反射信号与地震反射波信号在波的类型和频率上存在显著的差异。但针对f-k滤波器设计，只需考虑两种信号在频率方面的差异，即地震信号的频段通常为100Hz以内，而探地雷达信号的频率达50MHz以上。因此，根据探地雷达数据中有效回波和噪声在f-k平面上的分布特征，设计扇形滤波器进行滤波如图1所示。

图1 扇形滤波器示例

设计的滤波器还必须满足如下条件

(4)

其中，有效区为图1中灰色部分，及有效回波主要的f-k谱能量分布区。

1.3 探地雷达数据的f-k滤波流程

依据离散傅里叶变换的原理和扇形滤波器设计的方法，本文建立探地雷达数据f-k滤波的流程如图2所示，具体可分为三步：

1)读取探地雷达剖面数据，利用二维离散傅里叶变换计算数据的f-k谱；

2)根据数据的f-k谱特征，设计合适的扇形滤波器，并与探地雷达数据的f-k谱相乘，得到滤波后的f-k谱；

3)利用二维离散傅里叶反变换将滤波后的f-k谱转换成滤波后的探地雷达剖面输出显示。

图2 探地雷达数据f-k滤波的流程

2 滤波效果分析

2.1 含噪声正演记录的滤波效果分析

图3(a)所示为常见探地雷达数值模型的正演记录，图3(b)为加入高斯白噪声后的正演记录(信噪比为10，峰值信噪比为11.77)，所示噪声对有效回波产生了干扰，“掩盖”了部分有效回波的细节，影响有效回波的准确识别，如图3(b)箭头所示。

图4所示为正演记录f-k谱的正周期和主周期，可以看出，有效回波的f-k谱能量主要集中在f轴附近的扇形区；图5所示含噪声记录的f-k谱中，有效回波的能量部分被噪声的能量“掩盖”；正演记录f-k谱原先没有能量的位置受到噪声的干扰，也存在一定值的能量。

(a)原始正演记录 (b)含噪声正演记录图3 正演记录与含噪声正演记录

(a)正周期 (b)主周期图5 含噪声正演记录的f-k谱

依据图1设计扇形滤波器，从含噪声记录的f-k谱着手进行滤波，滤波后的f-k谱如图6所示，扇形滤波窗以外的f-k谱能量为0，与原纪录一致，扇形滤波窗以内的位置多为有效回波的f-k谱能量，得以保留。通过离散的二维傅里叶反变换得到滤波后的记录如图7所示，图中的记录相对于图3(b)记录在细节上有了很大的改善(如图7中箭头所示)，滤波后的记录峰值信噪比为22.84，相对于含噪声正演记录的峰值信噪比显著提高。

图6 滤波后的f-k谱

图7 f-k滤波后的正演记录

2.2 实采探地雷达剖面的滤波效果分析

在某高校的地质工程实验场地采集的探地雷达剖面经过球面扩散补偿后如图8(a)所示，在扩散补偿的过程中有效回波得到了增强，但噪声干扰也随之增强，造成图像下部的有效回波信号被噪声部分“掩盖”，有效信号识别难度加大，很难基于该记录进行有效的解释。不仅如此，从对应的f-k谱(见图8(b))同样可以看出， 在频率0～2GHz、 波数0～120的范围内噪声的f-k能量与有效回波的能量部分混叠在一起。

(a)实采探地雷达剖面

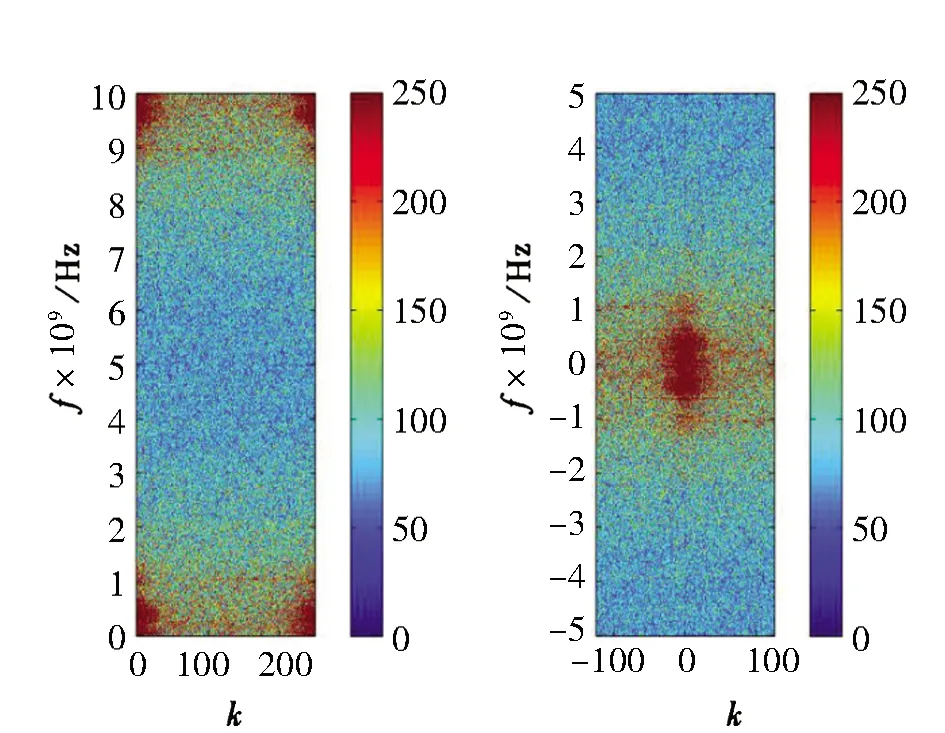
(b)f-k谱图8 实采探地雷达剖面及其f-k谱

设计如图1所示的扇形滤波器进行实采数据的f-k滤波，滤波后的探地雷达剖面及其与原记录的残差分别如图9和图10所示。图9中，滤波后剖面上部的有效回波基本不受影响，残差普遍小于0.2，而剖面中下部原先受噪声影响严重的位置，噪声得以较好的滤除，残差普遍在0.5左右，部分有效回波得以突出，能有效的进行识别，如图9中箭头所示。

图9 f-k滤波处理后的探地雷达剖面

图10 f-k滤波后的残差

3 结论

为了减小噪声对探地雷达数据中有效回波的干扰，提高有效回波的识别与解释精度，本文借助于地震数据处理中的f-k滤波方法进行探地雷达数据的滤波处理，得到如下结论：

(1)探地雷达有效回波的f-k谱能量集中在频率轴附近的扇形区域，借助于扇形滤波器能有效滤除正演记录中的噪声；利用含噪声正演记录测试表明，经过f-k滤波后，地震记录的峰值信噪比从11.77增加到22.84。

(2)实采探地雷达剖面的f-k谱中有效回波能量与噪声能量存在部分混叠， 通过设计针对性的扇形滤波器， 并对比分析滤波后的剖面与残差， 发现f-k滤波方法对记录剖面中下部的噪声能有效的滤除，残差值达0.5左右；剖面上部有效回波基本不受影响，而原先下中部被噪声“掩盖”的有效回波能得以突出。因此，可以认为f-k滤波方法在压制探地雷达数据中的噪声，提高资料信噪比方面效果显著。