基于组合非线性反馈的机器人鲁棒控制方法*

公成龙，蒋 沅，2，代冀阳，2

（1.南昌航空大学信息工程学院，南昌 330063；2.南昌航空大学无损检测技术教育部重点实验室，南昌 330063）

0 引言

机器人系统是一个多输入多输出强耦合的非线性不确定系统。轨迹跟踪是机器人自动控制系统的主要工作任务之一，其方式和目的在于通过给定各关节的驱动力矩，使得机器人的位置、速度等状态变量跟踪给定的理想轨迹。

机器人有多种控制方法［1］，主要包括：计算力矩控制、自适应控制、最优控制、鲁棒控制、模糊控制、神经网络控制、反演控制、模糊控制、变结构控制、迭代控制等。

但是，在实际中机器人系统会存在一些不确定因素，如关节间的摩擦和外界扰动等，这些因素都会影响机器人的控制性能，故必须在设计机器人控制器的过程中考虑相应的对策以减少这些因素对机器人系统的影响。

组合非线性反馈理论（CNF）［2］是用来求解饱和系统定点跟踪任务的一种有效方法，由线性反馈控制和非线性反馈控制组成，线性反馈控制的目的是保证系统有快速响应，故它的作用是使系统有较小的阻尼率；非线性反馈控制可以使系统有快速响应的同时也能有较小的超调，其作用特点是使系统的闭环阻尼可调，即当系统的输出逼近参考输入时控制器可自动调大系统阻尼，使超调降低。文献［3］验证了组合非线性反馈控制在定点跟踪任务中控制性能优于时间最优控制。当系统中有由于扰动产生的误差时，强化CNF［4］（Enhanced CNF）控制方法利用积分环节作用进行消减，但是，积分环节所具有的缺点是只能处理定常扰动，当扰动非定常时，强化CNF 控制性能便不具备较优的鲁棒性。

Chen［3］将可测量的反馈项加入在原始的CNF控制器中，使CNF 控制器可以应用于一般的输入饱和系统中。但当系统中存在干扰时，CNF 控制作用下的系统便不再具有输出准确渐近匹配参考输入的能力。为解决这个问题，可以将扰动环节利用观测器［5］重构，用来补偿扰动的影响，进而改善了系统的跟踪性能，即在原有CNF 控制结构中加入干扰估计补偿项，形成基于组合非线性反馈的鲁棒控制器。

1 机器人鲁棒组合非线性反馈控制器

机器人系统的特点是多输入多输出且关节间存在强耦合。必须把基于组合非线性反馈的鲁棒控制器推广到多输入多输出的饱和系统［6］中，才能在机器人控制系统中应用并改善系统的控制性能。

N 个串联连杆的刚体机器人动力学模型为

其中，u 为外界控制输入量，用来抵消摩擦等扰动项f 对系统产生的影响。换句话说，u 就是所利用的新型控制律。

由式（2）、式（3）可得系统的动态误差方程为

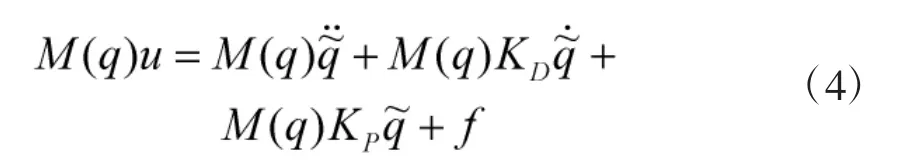
或

将其转换为状态方程为

将机器人完全动力学模型和基于组合非线性反馈的鲁棒控制器结合，得到基于计算力矩的新型机器人控制器

下面给出新型控制器下的系统稳定性分析。

定理 如果下列条件成立：

1）存在c＞0，满足如下约束：

定义Lyapunov 函数

所以系统稳定，证毕。

2 仿真分析

本文选取文献［7］中的机器人模型。

驱动力矩的上限是

为使得系统有快速相应，低增益线性反馈增益矩阵需使闭环系统获得较小的阻尼率。当增益矩阵KP和KD为相应的对角正定矩阵时，闭环系统为解耦的饱和线性系统，就需要机器人系统各关节所对应的自然频率和阻尼率与低增益矩阵有如下关系：

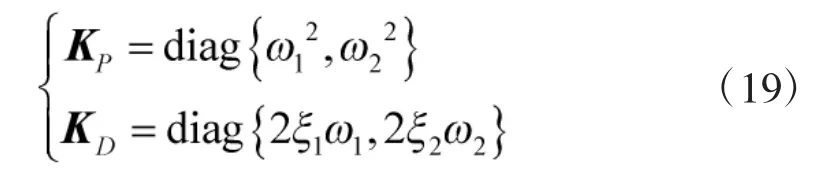
确定P 后，根据

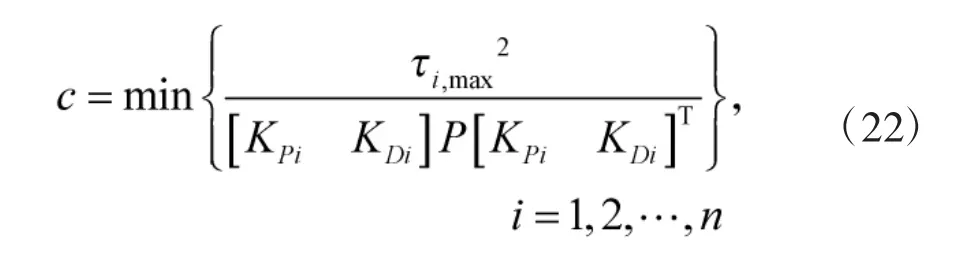
机器人系统在不同控制器下的仿真结果如图1至图6 所示。图1 和图2 是当存在摩擦等扰动时系统在原始组合非线性反馈控制下的仿真结果。虽然它能够保证驱动力矩在限制范围之内，但驱动力矩调整至稳定的时间过长，且跟踪至稳定过程时间长，误差较大，有较大超调，系统的鲁棒性一般，现实中无法接受。

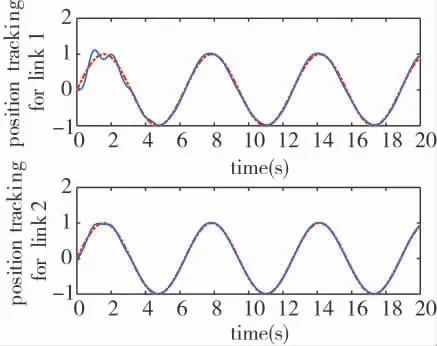
图1 原始CNF 控制下各关节跟踪结果

图2 原始CNF 控制下各关节的驱动力矩

图3 至下页图5 是系统在基于组合非线性反馈的鲁棒控制下的仿真结果，不仅快速响应、超调微小、能保证驱动力矩在限制范围内，而且在速度跟踪时快速又无明显误差，驱动力矩调整至稳定时间较原始组合非线性控制方法大幅缩减，鲁棒性较佳。

图3 新型控制器下对关节1 的位置和速度跟踪

图4 新型控制器下对关节2 的位置和速度跟踪

图6 是系统在基于组合非线性反馈控制下的扰动观测及补偿，快速且可调，可以持续地向系统提供力矩补偿，为机器人系统获得最佳的控制性能提供保障。

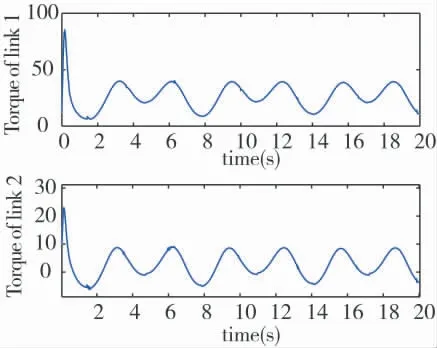
图5 新型控制器下各关节的驱动力矩

图6 新型控制器对各关节的扰动观测及补偿

综上所述，对比不同控制器的控制性能，基于组合非线性反馈的鲁棒控制器具有最快的调整时间和最小的超调及误差，动态性能最佳，有较强的鲁棒性，可以应用于机器人控制系统中。

3 结论

关节空间的轨迹跟踪是机器人控制的一个基本任务，目标是给定参考轨迹，通过设计控制器，使机器人末端执行器渐近跟踪参考轨迹，尽量使跟踪过程快速且轨迹光滑并抑制超调。本文通过CNF 算法设计的新型机器人模型控制器取得了预期效果，使得机器人系统具有准确的跟踪能力和较强的鲁棒性。故本文可以证明利用该方法控制机器人输入饱和系统，能保证系统的渐近稳定，且能够快速、准确地解决系统对时变轨迹的跟踪问题，大大提高系统的稳态性能、跟踪性能和鲁棒性能，下一步可考虑在工业中应用。