体现学段特征，渗透研究“套路”

刘东升

摘要：受到基于“数学现实”引入新知的教学研究和实践的启发，教学七年级《直线、射线、线段》一课时，精心预设画图活动引入并驱动全课学程。该课的主要教学立意是体现学段特征、渗透研究“套路”。

关键词：《直线、射线、线段》 学段特征 研究“套路” 留白式活动单

近年来，基于“数学现实”（相对于“生活现实”而言），即基于数学知识的前后一致、逻辑连贯，抓住数学对象的研究方法或基本“套路”，精心设计教学情境，引入新知的教学研究和实践，受到关注和重视。受此启发，笔者最近开设一节七年级《直线、射线、线段》研究课时，精心预设画图活动引入并驱动全课学程，达成了较好的教学效果。下面梳理该课教学流程，并阐释教学立意，提供研讨。

一、教学流程

课前，教师印发留白式活动单给学生。活动单包括四个部分：“课题”（留白），“画图并表述”（给出A，A、B，A、B、C三组点，其他留白），“新知结构图”（提示“直线”“图形”“表示”“性质”，其他留白），“小结与练习”（给出3道习题，其他留白）。课堂教学环节如下：

（一）经过一点、两点画直线

引入：进入初中，同学们将系统学习平面几何，就让我们从几何图形的基本元素——点开启学习之旅。我们知道“点动成线”，线又有直线和曲线。本着从简单开始的原则，我们先研究直线及相关概念。

画图：经过点A作直线。

教学组织：请一名学生上台板演，其余学生在活动单的“画图并表述”部分完成。如果学生只作出一条直线，则追问：是否还能作出直线？还能作出多少条直线？学生很快确认：还能作无数条直线。教师在图的下面板书：经过一点可以作无数条直线。

画图：经过点A、点B作直线。

教学组织：请一名学生上台板演，其余学生在活动单的“画图并表述”部分完成。学生很快确认：经过点A、点B只能作出一条直线。教师追问不同的学生，反复确认这一事实。然后，在图的下面板书：经过两点有一条直线，并且只有一条直线。

（二）建立新知结构

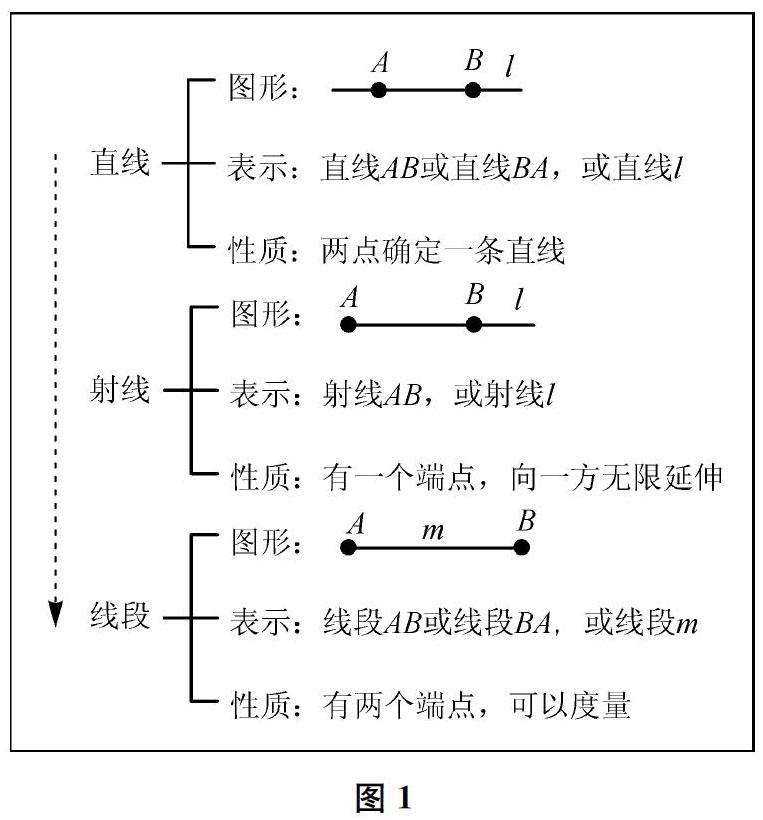
谈话：学习几何的关键是能对图形进行精准表述。而为了表述一个图形，则需要对图形进行规范的表示。（同步画图、板书）比如，刚才大家在画图过程中得到的直线，就可表示为直线AB、直线BA，也可用一个小写字母l来表示，即直线l。

提问：黑板上经过一点画直线、经过两点画直线，得到两幅图形，还有其他的表述方式嗎？

引导：比如，点A在直线l上，直线l经过点A，直线AB经过点A、B，点A、B都在直线l上，等等。

谈话：直线上一点及其一边部分称为射线。（同步画图、板书）表示为射线AB或射线l，这里表示端点的字母需要写在前面;射线的性质是，有一个端点，向一方无限延伸。

谈话：直线上两点及其之间部分称为线段。（同步画图、板书）表示为线段AB、线段BA，也可用小写字母表示为线段m;线段的性质是，有两个端点，可以度量长度。

由此，教师渐次生成研究直线、射线、线段的图形、表示、性质的结构化板书，如图1所示。学生相应地在活动单上完成“新知结构图”。

（三）经过三点画直线

画图：经过平面内三个点A、B、C画直线。

教学组织：先安排学生思考经过三个点能否画出一条直线。学生会“惯性”地说不可能。教师要指出，有一种特殊情形，就是三个点在同一直线上。然后，安排学生经过其中两点画直线，并思考共能画几条。请一名学生上台板演，其余学生在活动单的“画图并表述”部分完成。

表述：请同学们把目光投向画出的图形（如图2），这个图形的表述有哪些不同的方式？

教学组织：学生先在小组内交流，再面向全班汇报。学生会有点A在直线AC、AB上，点B在直线AB、BC上等不同的表述。最后，教师给出一种更为简洁的表述：三条直线两两相交于A、B、C三点;并进一步讲授：两条直线有且只有一个公共点时，称这两条直线相交，这个公共点为它们的交点。

（四）小结

谈话：同学们，今天我们来一次特别的课堂小结。大家看活动单上的“课题”，是不是空着没写？现在就请各人结合本课所学，为本课拟一个课题。

教学组织：安排学生先在小组内交流分享各自拟订的课题，然后推荐到全班展评，最后选定一个得到大家认可的课题，书写到黑板上。

（五）练习

1.要钉一根水平方向的木条，至少需要__________个钉子，其理论依据为______________。

2.如图3，下列几何语句表述错误的是（ ）

A.点A在直线a上

B.点A在直线b上

C.点B在直线a上

D.直线a不经过点B

3.根据下列语句画出图形：（1）直线EF经过点C;（2）点A在直线l外;（3）经过点O的三条线段a、b、c;（4）线段AB与直线CD相交于点B。

设计意图：通过练习反馈学生对本节课教学重点的掌握情况。第1题主要检测学生对“直线公理”的理解;第2题是读图，理解不同表述并辨析错误表述;第3题是读表述，画出符合要求的图形。

二、教学立意

（一）体现学段特征

在小学，学生已经学过“直线、射线、线段”的有关内容，对直线的延伸性、射线和线段的直观特性已有了解。在初中，学习“直线、射线、线段”是系统、全面学习平面几何的起始，主要内容源自《几何原本》，主要价值是数学的理性精神。所以，备课前要认真思考怎样上得与小学阶段不一样，体现初中学段特征，并找准教学用力点。比如，研究一个数学对象，需要关注它的定义、表示方法（对于图形来说，特别是符号语言表示方法）、性质等。这些都是初中阶段“直线、射线、线段”教学的重点与难点。辨析以上学段特征后，我们就能知道有些“生活味”太浓的情境在初中阶段需要适当淡化，或仅在练习环节简要提及，不宜成为开课情境，占据太多教学时间。

（二）渗透研究“套路”

章建跃先生指出：“数学育人要用数学的方式，要发挥数学的内在力量。如数学的思考结构具有系统性、普适性，其基本套路大致可以概括为‘抽象数学对象一探索数学性质一构建知识体系。数学的思维方式具有结构性、一致性、连续性，数学的表达方式具有统一性，使用一套世界通用的符号形式进行交流……”数学的思考结构、思维方式和符号化表达正是数学的力量所在。这样来看，平面几何起始阶段的教学就要注重渗透几何的研究“套路”。这些研究“套路”可以从以下方面梳理：（1）几何研究一个对象的形状、大小、位置。如本文课例，研究了点和直线、直线和直线的位置关系。（2）几何研究往往沿着“定义-符号表示-性质-判定”的路径展开。如本文课例，依次研究了直线、射线、线段的定义（遵循教材设计，以一个形象的图形代替，没有给出严格的定义）、多样化的符号表示、性质（特征）;因为这三种图形十分简单，是后续组成更复杂图形（如角、三角形、多邊形等）的基本元素，所以，没有判定方法。（3）几何研究往往从一般到特殊。如本文课例，先研究直线（一般），再研究它的“部分”：射线和线段（特殊）。从而让学生感受到射线、线段与直线之间的特殊与一般的关系。综上，几何学习与研究可以有多种“套路”，要根据教学内容深入构思、灵活选用（笔者曾有课例实践与解读，比如，对一些更复杂的几何图形，如三角形、四边形，还需要研究它们的相关元素，如边、角、角平分线、对角线等）。可以这样说，能否以研究“套路”相机引导学生自主探究并驱动学程不断深入，可以体现出教师对数学教学内容的理解程度。

此外，特别需要指出的是，当前不少城区的“规模学校”（一个年级往往达到15个平行班以上）普遍使用所谓的“导学案”，驱动和引领课堂教学。这类导学案一个饱受争议的问题是，选用大量的习题，使教学处于“离开教材学数学”的尴尬境地。这种“习题单式”的导学案引发了不少专家、学者的一些忧虑。而本文课例教学手段上的一大亮点就是反复打磨形成的留白式活动单和结构化板书。这份“极简”的活动单是从大容量的知识点、习题式的导学案精简而来的。学生拿到这样的活动单后，对本课要学习的内容是充满好奇的。课堂上，随着画图活动、新知生成，展现了师生共同“探索未知世界”的一种研究范式。另外，随着教学进程渐次生成结构化板书，学生既学到了新的知识，又感悟了几何研究的方法与“套路”。