多层隔热装备的热防护性能与优化设计

杨哲瑜 曾思怡 余冠辰

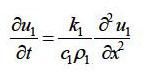
摘要：本文建立了热防护服的四层热传导模型，利用古典显式差分法对工况1进行MATLAB求解，研究其热防护性能;同时采用粒子群算法对工况2下防护服的厚度进行优化设计。研究得到工况1下各层的温度分布并绘制温度分布图，工况2下防护服第三层的最优厚度。本文研究内容对于热防护服的设计具有一定借鉴意义。

关键词：热传导模型;古典显式差分法;粒子群优化算法

一、引言

近年来，森林火灾发生频率激增，不断吞噬消防员的生命， 因此对于高温作业下热防护服的优化设计显得尤为重要。关于 热防护服的设计，国内外许多的学者做了大量的研究。不同于 以往研究，本文主要用假人的体温变化来研究在特定边界条件 下防护服的的热防护性能，利用有限差分法求解抛物型偏微分 方程并得到温度分布三维图;采用粒子群算法优化算法来计算 体温条件下的 II 层的最优厚度。

二、工况设定与模型建立

2.1 工况设定

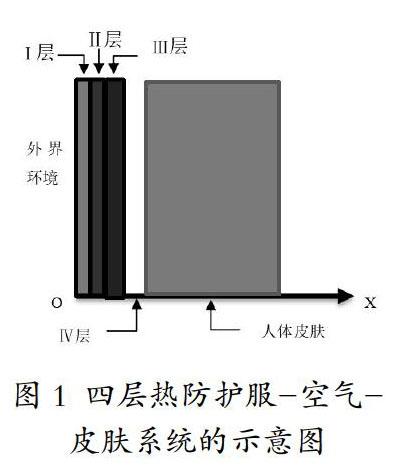
本文工况测试选取专业服装材料及假人皮肤外侧温度变 化。专用服装通常由三层织物材料构成，记为第 I、II、III 层， 其中 I 层与外界环境接触，III 层与皮肤之间存在空隙，将此空 隙记为 IV 层。

工况 1：对环境温度为 75?C、人体温度 37?C、第 II 层厚度 为 6mm、IV 层厚度为 5mm、工作时间为 90 分钟的情形开展 实验，得到假人皮肤外侧的温度。

工况 2：当环境温度为 65?C、IV 层的厚度为 5.5mm，假 人皮肤外侧温度不超过 47?C，且超过 44?C 的时间不超过 5 分 钟。

2.2 模型设定

2.2.1 热传导模型的建立

首先建立四层热防护服-空 气-皮肤系统的示意图如下： 现在要模拟热量通过高温 作业服的过程。参考一维热传导 方程的推导，可得Ⅰ层织物的热 传导方程为：

同理，将上式推广到i 层织 物材料，得到各层的热传导方程：

我们设定：相邻两层材料之间，左侧材料的右底面与右侧 材料的左底面温度相等。

由此得到数学模型：

2.2.2 边界条件的设定

Ⅰ层与外界环境直接接触的面，温度与外界环境相同：  ， 人体表面温度关于时刻值 t 的函数为 a（t），Ⅳ层右 底面与人体表面直接接触的面，故温度与人体表面温度相同：

2.2.3 差分求解

三、结果分析

3.1 工况

1 下防护服的热防护性能 工况 1 下，我们取左边界温度为 75℃，右边界温度分布为 a，初始空间步长 0.01 h ，时间步长 1  ，对热传导的四阶抛 物型偏微分方程组进行 MATLAB 编程求解，得到 t x 平面 上的温度数据并绘制在时空上的分布图。由计算结果得到，第 Ⅰ层温度稳定于 75℃，第 II 层稳定于 74.94℃，第 III 层稳定于 67.85℃，第 IV 层稳定于 47.87℃。

3.2 工况 2 下防护服的最优厚度

粒子群算法，又称 PSO 算法，PSO 初始化为一群随机粒子 （随机解），所有粒子都遵循一个由被优化函数所确定的适值， 每个粒子还有一个速度决定它们的飞行方向与距离。所有粒子 都追随着当前最优粒子的搜索区域在空间中进行搜索，然后通 过迭代找到最优解。在每一次迭代中，粒子通过追踪两个极值 来更新自己;第一个是粒子本身所找到的最优解;另外一个是 整个种群中目前找到的最优解，这个极值就是全局极值。

由于差分方程的递推性，可由处于 1 j 时的u 值来推导得 到 j 位置的u 值，所以通过不断递推，可通过于已知的 0 m 时的一系列初值来建立一个由 x L2 为自变量，皮肤表层温度即 hLLxLLj /）4321（ 的函数关系。将该关系作为 PSO 模 型中的待优化函数。并将种群规模设置为 5，将进化次数设置 为 20 次通过 Matlab 编程的 PSO 算法进行求解。得到的待优化 函数粒子进化與厚度适应关系。最终得第二层的最优厚度为 8.817mm。

参考文献：

[1]张庆科. 粒子群优化算法及差分进行算法研究[D]. 山 东大学，2017.

[2]贾海峰. 一维热传导方程的推导[J]. 科技信息， 2013（02）：159.

[3]消防员个人防护装备[J]. 安防科技，2013（01）：36-37.