具有平行平均曲率向量的伪脐子流形

温焕明，陶炎芳

(1. 江西科技学院，330098，南昌；2.南昌师范学院附属中学，330029，南昌)

0 引言

对于Nn+p中具有平行平均曲率向量的伪脐子流形，有如下定理。

定理A[1]:设Mn是Nn+p中具有平行平均曲率向量的紧致伪脐子流形，若Mn的Ricci曲率Rii满足

则Mn是Nn+p的全脐子流形。

本文根据定理A中的情形研究了局部对称空间具有平行平均曲率向量的伪脐子流形，得到这类子流形关于第2基本形式模长平方σ和RicciQ的一个拼挤定理。

1 预备知识

又设Nn+p是局部对称空间，即KABCD,E=0，其中KABCD,E是Nn+p的曲率张量KABCD的共变导数，且约定指标的取值范围为

1≤A,B,C,…≤n+p;1≤i,j,k,…≤n;n+1≤α,β,γ,…≤n+p。

设Mn是等距浸入在Nn+p中的n维紧致子流形，在Nn+p上选取局部正交标架场{eA}，使得它限制在Mn上，{ei}切于Mn。设{ωA}是eA的对偶标架场，{ωAB}是Nn+p的联络形式，则限制在Mn上，有

(1)

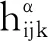
(2)

以下总假设Mn具有平行平均曲率向量，则

(3)

又Nn+p是局部对称的，则

(4)

式中：Kαijkl为Kαijk的协变导数。以下总选取en+p与ξ的方向相同，则

(5)

由式(1)、式(3)、式(4)、式(5)，经计算

(6)

(7)

于是，由式(1)、式(6)，对于任何实数a，有

(8)

为了后面的证明，引进2个引理：

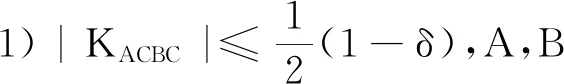
2 定理的证明

定理：设Mn是局部对称的δ-Pinching黎曼流形Nn+p中的具有平行平均曲率向量的紧致伪脐子流形(p≥2)，若

则Mn是Nn+p的全脐子流形。

证明：在式(8)中取a=-1,则有

(9)

由引理1和引理2可得：

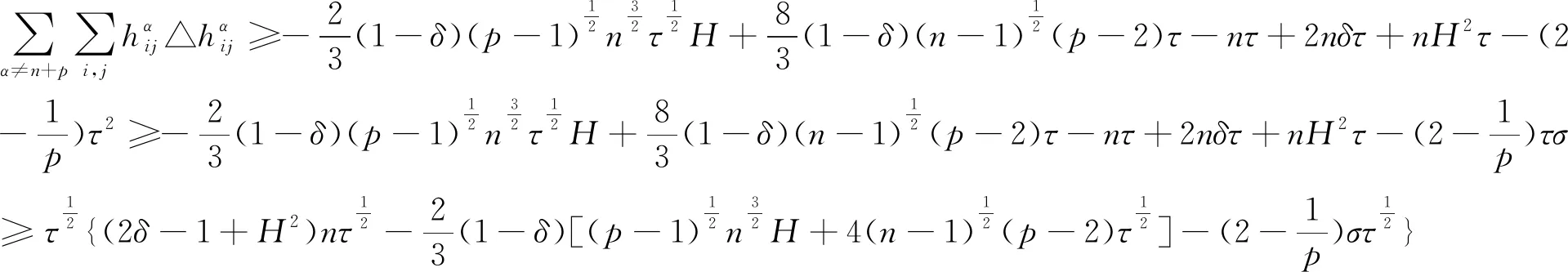
(10)

所以在定理的条件式有：

(11)

因Mn紧致以及Hopf极大值引理得τ为常数，再由式(10)、式(11)得τ=0，即

(12)

或

(13)

当式(13)成立时，上面各式均取等号，由式(10)取等号得δ=1，从而式(9)为：

(14)

此时由定理A和文献[2-3]，易见τ=0，再由式(6)知，Mn是Nn+p的全脐子流形。