基于DBSCAN算法的浮动车数据预处理

张 昀，李小龙

(东华理工大学测绘工程学院，330013，南昌)

0 引言

浮动车一般是指行驶在城市道路上并安装了车载GPS定位装置的公交车或出租车。在浮动车行驶过程中，车载GPS会定期记录该车辆的位置、方向和速度等信息，这些信息集合称为浮动车数据。随着城市里出租车数量的和运营里程的不断增加，聚集了海量的浮动车数据。通过挖掘浮动车数据，可以得到城市道路特征和城市交通特征等信息[1]。

高质量数据是数据挖掘的重要保证，“脏数据”会导致输出错误。因此，数据预处理已成为人们提高数据挖掘质量的主要研究方向之一。脏数据是指原始数据超出指定范围或对于后续的应用毫无意义的数据，或者是数据有缺失[2]。原始浮动车数据的观测误差主要来源于多路径效应、大气延迟和衍射等方面。多路径效应广泛存在于各类复杂交通环境中，特别是在高楼耸立的城市经济中心和交错复杂的立交桥区域，高层建筑和立交桥都会成为反射物，干扰卫星信号的接收，产生衍射误差[3]。另外，高压电力线、电塔和避雷针对GPS信号也会有较大的影响[4]。上述误差的存在将严重影响浮动车数据的质量，造成浮动车数据点轨迹漂移，从而降低数据挖掘的效果。因此，数据预处理方法研究意义重大，同时也面临诸多挑战[5-6]。

目前，关于浮动车数据预处理的方法有很多。王德浩[7]等将浮动车数据转换为多分辨率轨迹图像，然后使用数学形态滤波的方法对图像进行去噪、平滑和增强处理。唐炉亮[8-9]等提出了以Delaunay三角网的三角形面积和边长为约束条件进行浮动车数据清洗。汪宏宇[10]等提出基于小波阈值去除噪声，并从阈值、阈值函数的选择、小波基的选择、小波分解层数4个方面来研究适合于浮动车数据的小波去噪算法。Liu[11]等提出一种新型时空粒子滤波器ST-PF，并将其与均值滤波器、中值滤波器、卡尔曼滤波器和原始粒子滤波器进行比较，结果表明，ST-PF在降低噪声和提高地图匹配性能方面更有效。Li[12]等通过自适应密度优化方法对浮动车数据进行预处理，以获得高质量的浮动车数据。本文提出了一种基于DBSCAN算法的浮动车数据预处理方法，该算法是一种基于密度的空间聚类算法，能在具有噪声的空间数据中发现任意形状的簇，适用于像车道这样的长条形。而且该算法运算速度快，精度高。

1 浮动车数据预处理

浮动车数据可在城市道路信息提取、交通分析、智慧城市研究等领域发挥重要作用。主要有以下3个方面的原因：1)覆盖面广，每天都有数万辆出租车在城市的大街小巷上行驶，海量的浮动车数据布满城市的每个车道，因此其产生的时空数据可以基本覆盖整个城市；2)实时性强，道路上行驶的浮动车以40 s左右的频率24 h不间断采集数据，并实时上传到交通管理中心；3)数据量大，例如武汉市有1.2万多辆出租车每天可以产生4 000万条数据[13-14]。由于采集环境和采集设备等限制，使得原始浮动车数据中含有大量噪声，因此需要对其进行预处理，流程如图1所示。

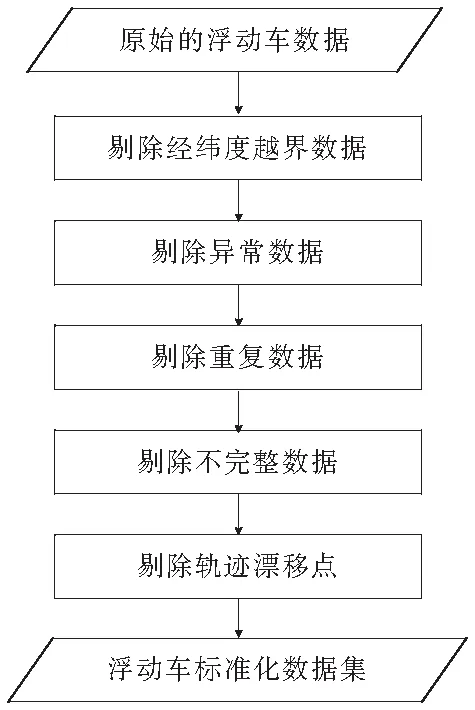
图1 数据预处理流程图

数据预处理主要是将原始浮动车数据中的经纬度越界数据、异常数据、重复数据、不完整数据和轨迹漂移点剔除，从而得到一个浮动车标准化数据集。本文根据研究内容对浮动车GPS数据制定了以下几种处理数据的规则[15]。

1.1 剔除经纬度越界的数据

本文以武汉市为研究区域(该研究区域的地理位置是北纬N29°58′～31°22′，东经E113°41′～115°05′即一个矩形)，在数据库中剔除超过武汉市城区范围的数据。浮动车数据包括当前车辆位置的纬度和经度、载客状态、时间、行车方向、速度等信息。先新建一个数据表并把数据按相应格式导入数据表中，然后在数据表中将超出经纬度范围的数据剔除。图2是浮动车数据在区域内道路上的分布图，每个圆点代表某辆浮动车在某时刻的瞬时位置。

图2 浮动车数据在区域内道路上的分布图

1.2 剔除异常数据

出租车载客状态分为“0”和“1”，其中“0”代表空载，“1”代表载客。异常数据包括以下3种情况：载客状态非“0”和“1”的数据显然是错误的，此类数据应该删除；出租车全天空载，载客状态全天为“0”，这类数据没有研究意义，应过滤；出租车全天载客，载客状态全天为“1”，通常，这种情况的出现几率几乎为零，可能是由于设备故障或者人为因素导致的，此类数据会影响后续的分析，会导致结论错误，应该删除。

1.3 剔除重复数据

重复数据是指多条数据各个字段值完全相同的一类数据，这类数据往往只有一条具有研究意义，其他数据的出现都是错误的。在后续的数据挖掘和分析中，多条重复数据的存在会降低算法和模型的有效性，并影响研究结果，因此应该剔除此类数据。本文在数据库中使用SQL语句对原始数据集中的重复数据进行剔除。

1.4 剔除不完整数据

原始浮动车数据的记录中，可能存在缺失字段的记录，比如某条数据记录的速度值为空。在出租车GPS数据中ID、经纬度、时间、速度、载客状态等其中任意一个字段或多个字段的缺失对后续的数据挖掘和分析都会产生影响。因此在数据预处理时，将缺失数据的记录全部剔除。

1.5 剔除轨迹漂移点

当浮动车行驶在高楼大厦或立交桥附近时，或者车载GPS发生故障，都会导致GPS轨迹数据漂移。采取DBSCAN聚类算法找出轨迹漂移点并将其剔除。DBSCAN是一种基于密度的聚类算法[17-18]。该算法的聚类过程是将密度相连的点集合为簇，直到所有的数据都处理完毕，可以得到最后的聚类结果簇。DBSCAN算法可以在具有噪声的空间数据集中找到任意形状的聚类结果簇，并将每个样本点分为核心点、边界点和噪声点[19]。因此，该算法近年来受到广泛关注，并被应用到图像处理和数据清洗(双酚A生产数据清洗)等领域中[20]。本文以浮动车的纬度和经度数据作为样本，找出浮动车数据中的漂移点。

采用DBSCAN算法对浮动车数据进行剔除轨迹漂移点处理，主要的参数为Eps和MinPts。Eps领域意指某点以Eps为半径的领域。MinPts(领域密度阈值)是指某点Eps领域内点的数量。这2个参数对聚类效果影响很大，即使细微的变化，也会对结果产生很大的影响。当前，对这2个参数的选择无有效依据，只能通过个人经验或多次实验来确定。如图3所示，当MinPts=6，则点A为核心点，点B为边界点,点C为噪声点。其中对于浮动车数据分布密度高的区域， Eps邻域包含的点数大于或等于MinPts值，而对于浮动车数据分布密度低的区域，Eps邻域包含的点数小于MinPts值。由于DBSCAN算法能将这两类点快速准确的区分开，因此本文采用DBSCAN算法剔除轨迹漂移点。该算法具有聚类速度快且能够有效识别噪声点、能发现任意形状(非凸，互相包络，长条形等)的空间聚类、不需要指定簇的个数等优点。

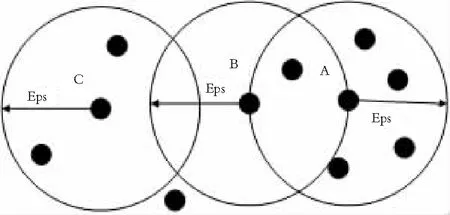
图3 核心点、边界点和噪声点示意图

2 实验结果与讨论

对采集到的武汉市浮动车数据进行筛选后，在研究区域内随机选取了50条宽度不同的道路进行实验。首先在数据库中进行经纬度越界数据剔除、异常数据剔除、重复数据剔除、剔除不完整数据等处理。接着将处理后的数据可视化，如图4所示，图中单个点代表某辆出租车在某个时刻的位置，细的线条为道路中心线，粗的线条为道路边界线，道路边界线是参考百度地图街景上与之相对应的车道宽度绘制出来的。从图4中可以看出，浮动车数据基本服从高斯分布，越接近道路中心线的浮动车数据分布越密集，越往两侧分布越稀疏。这些浮动车数据的分布宽度明显要大于车道的实际宽度，表明这些浮动车数据中存在大量漂移点。

将2条道路上的浮动车数据分别存入Excel表，在MATLAB中写好的DBSCAN算法，设置参数，导入Excel表中的数据，运行程序。结果如图5所示，图5中“+”是核心点表示合格的浮动车数据，“·”是噪声点表示浮动车数据中的轨迹漂移点。

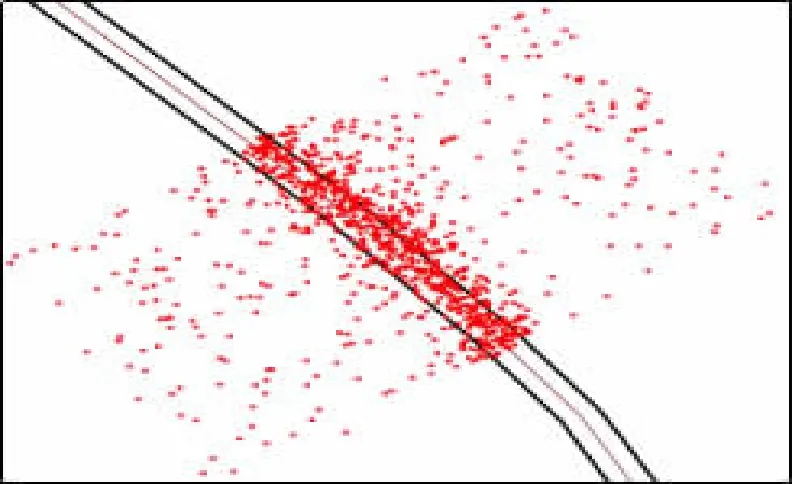
(a) 道路1

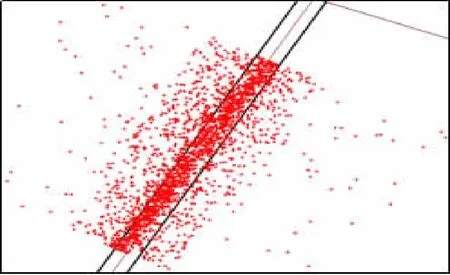
(b) 道路2

(a) 道路1

(b) 道路2

将处理后得到的浮动车数据与原始的浮动车数据进行对比，如图6所示，图6中密集圆点代表清洗后被清除的浮动车数据点，散布圆点代表清洗后剩余的浮动车数据点。从图6中可以明显看出，经过DBSCAN算法清洗后的浮动车数据大部分都分布在道路边界线以内，而清洗前的浮动车数据中有较多数据分布在道路边界线以外。

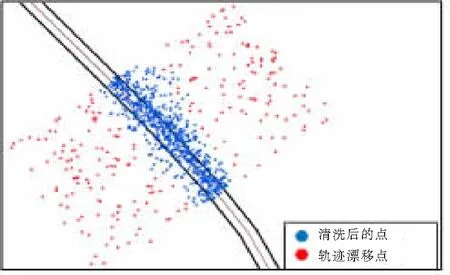
(a) 道路1

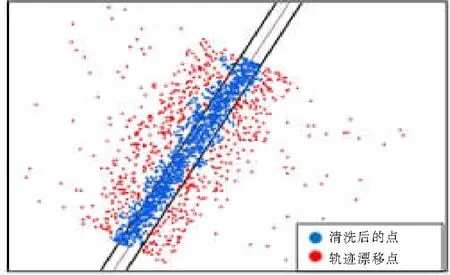
(b) 道路2

为了进一步验证算法的准确性，在50条道路中随机选取了2条道路并分别计算这2条道路清洗前后的浮动车数据的拟合度和准确率。拟合度指的是回归直线对观测值的拟合程度。可决系数R2是度量拟合度的统计量，R2最大值为1，R2越接近1说明回归直线对观测值的拟合程度越好，反之越差。由于浮动车数据中含有漂移点，漂移点会导致浮动车数据分布较散，即拟合度较低。可决系数的公式如式(1)所示：

(1)

其中：SSR是指回归平方和，SSE是指残差平方和，SST是指总离差平方和。

准确率指在道路边界线内的浮动车数据占道路上的浮动车数据的比例，准确率越高，表明道路上的浮动车数据中在道路边界线内的浮动车数据占比越高，清洗效果越好。准确率的公式如式(2)所示：

(2)

道路1和道路2清洗前后的拟合度和准确率如表1所示。从表1可知道路1和道路2的浮动车数据清洗后的拟合度比清洗前有明显提高，但准确率相比之前提高不明显。原因是在浮动车数据预处理中的前几步已经把大量低质量的浮动车数据剔除，而基于DBSCAN聚类算法剔除的漂移点相对较少。因此，可以证明本文提出的算法能够有效清洗浮动车数据中的漂移点。

表1 道路1和道路2清洗前后的拟合度和准确率

参数的不同，对数据的聚类效果也会有差异。DBSCAN的参数有Eps和MinPts 2个，其中Eps可以通过epsilon函数计算出来，因此只需调整参数MinPts。

%epsilon函数的功能：

%[eps]=epsilon(x,MinPts)

%目的：求解DBSCAN估计领域半径

%x- data matrix(m,n);m-精度，n-纬度

%MinPts - 邻域密度阈值

[m,n]=size(x);

Eps=((prod(max(x)-min(x)) * MinPts * gamma (.5 *n+1))/(m*sqrt(pi.^n))).^(1/n)

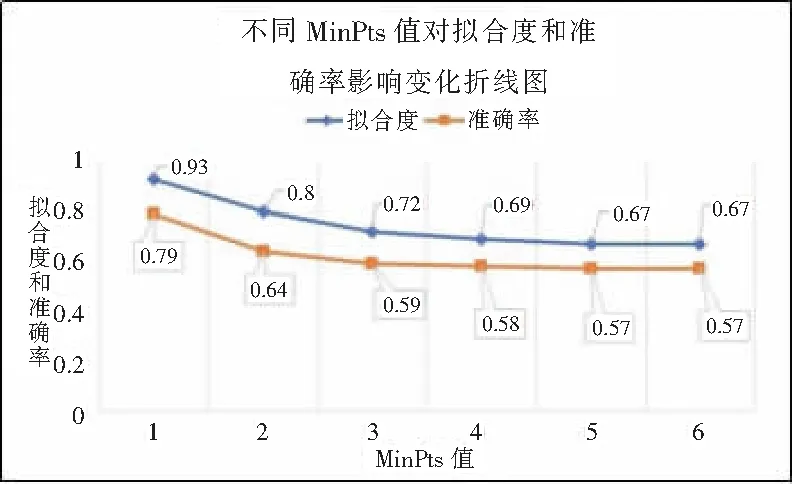
图7 不同的MinPts值对拟合度和准确率影响变化折线图

图7是不同的MinPts值对拟合度和准确率影响变化折线图，图7中横坐标是MinPts的数值，纵坐标是拟合度和准确率的值。从图7中可知，当MinPts值为1时，拟合度和准确率最高。当MinPts值为5和6时，拟合度和准确率最低而且相等。因此，选择MinPts值为1对浮动车数据进行处理。随着MinPts值的增大，一些漂移点被误判为合格的浮动车数据，随着合格的浮动车数据逐渐饱和，其拟合度和准确率将趋于稳定，不再发生改变。

3 总结与展望

分析了目前国内外浮动车数据预处理方法的基础上，提出了一种基于DBSCAN密度聚类算法的浮动车数据预处理方法。实验结果表明，该方法利用浮动车数据的空间分布特征成功剔除了浮动车数据中的大部分漂移点，且操作简单，运算速度快，准确率高。然而，此方法对十字路口和复杂交通路口的预处理效果不够理想。在未来的研究中将会对该方法做相应改进，并将进一步研究如何从浮动车数据中获取当前道路的交通状况和车道数量。