基于二次函数背景,探究角度的建构策略
2020-06-24开远市教科所赵宏伟
开远市教科所 赵宏伟
在近两年的初中数学学业水平考试压轴题中,以二次函数为背景,构造满足角度要求的直线成了新的考点.这类题目既考查锐角三角函数的应用,又考查灵活多变的构造方法,既能凸显学生的认知水平,又需要融入一些技能、技巧和方法.下面,笔者通过几个例题加以分析.
一、退守正切,构造角度
解析:由于∠BDC 是确定的角,我们需要探究一下∠BDC 的度数或它的某一三角函数值,才能方便地构造未知角.连接BC,考察△BCD 的形状.由可得点B 的坐标(4,0),由x=0 可得点C 的坐标(0,-4).又∵点D 的坐标是(1,-5),∴BC=,CD=,BD=.∴BC2+CD2=BD2.∴△BCD是直角三角形,tan∠BDC==4.要使∠MCE=∠BDC,只需要tan∠MCE=tan∠BDC=4.∵点M 在线段BD 上,∴设直线BD 的解析式为y=kx+b.把点B,D 的坐标代入这个解析式,得解得.∴直线BD 的解析式为.设点M 的坐标为(x,).∵∠MCD 是锐角,点C 的纵坐标为-4,∴yM 图1 方法感悟:求点M,使∠MCE=∠BDC,可以转化为探寻∠BDC的度数,进而可以转化为探究△BCD的形状.通过推理计算,我们得到的结论为∠BCD是直角.由于∠BDC不是特殊角,于是退而守之,将原问题转化为计算∠BDC的正切值问题.在直角三角形中,一个角的正切值等于角的对边比邻边,由此可以建立等量关系,进而可以列出方程,求出相关的量,最终使原问题得以解决. 图2 例2(2018·河南)如图2,抛物线y=ax2+6x+c 交x 轴于A,B 两点,交y 轴于点C,直线y=x-5 经过点B,C,过点A 的直线交直线BC 于点M.连接AC,当直线AM 与直线BC 的夹角等于∠ACB 的2 倍时,请直接写出点M 的坐标. 解析:∵直线y=x-5 经过点B,C,∴B,C 的坐标分别是(5,0),(0,-5).把这两个坐标代入抛物线的解析式,得解得a=-1,c=-5.∴抛物线的解析式为y=-x2+6x-5.∴点A 的坐标是(1,0),点B 的坐标是(5,0). 由构造的角度是已知角的2 倍联想到等腰三角形的顶角的外角是底角的2 倍,进而想到以∠ACB 为等腰三角形的一个底角构造等腰三角形,即可使原问题得以解决.如图3 所示,作线段AC 的中垂线,交BC 于M,连接AM,则MC=MA,∠AMB=2∠ACB,点M 即为所求.∵点M 在直线BC 上,∴设点M 的坐标为(x,x-5).∵MC=MA,∴(x-0)2+(x-5+5)2=(x-1)2+(x-5-0)2.解得x=.此时,y=x-5=.∴点M 的坐标是(). 图3 由于∠ACB 是锐角,我们还需要探究是否存在两解.过A 作AH⊥BC,垂足为H.∵OB=OC=5,∴∠OBC=45°,△ABH 是等腰直角三角形,H 在线段AB 的中垂线上.∴点H 在抛物线的对称轴上.∴点H 的坐标为(3,-2).∴AM>AH.∴在线段BC 上还存在一点M′满足条件,且M′与M 关于点H 对称,即∠AM′M=∠AMM′=2∠ACB.∴由对称性可得点M′的坐标(). 方法感悟:在构造二倍角时,等腰三角形奠定了思考方向和方法.在求解压轴题时,同学们只有提高了辨析力与反思力,并进行全面探究,才能防止漏解. 例3 (2019·贵州)已知抛物线y=ax2+bx+3 经过点A(1,0)和点B(-3,0),与y 轴交于点C,点P 为第二象限内抛物线上的动点,如图4,点E 的坐标为(0,-1),点G 为x 轴负半轴上的一点,∠OGE=15°.连接PE,若∠PEG=2∠OGE,请求出点P 的坐标. 解析:设抛物线的解析式为y=a(x-1)(x+3)=a(x2+2x-3),比较可得-3a=3.解得a=-1.∴抛物线的解析式为y=-x2-2x+3.∵∠OGE=15°,∴∠PEG=2∠OGE=2×15°=30°.∵∠OGE=15°,∴∠OEG=75°.又∵∠PEG=30°,∴∠PEO=45°.设PE 交x 轴于Q,则OQ=OE.∴点Q 的坐标是(-1,0).∴直线PE 的解析式为y=-x-1.由方程组得x2+x-4=0.解得x=.∵点P 在第二象限,∴舍去正值,保留负值,即x=.此时y=-x-1=.∴点P 的坐标是(). 图4 方法感悟:本题虽然是由特殊角转化到特殊角,但是需要由表及里,深入挖掘已知条件,认真观察图形,发现内在的等量关系.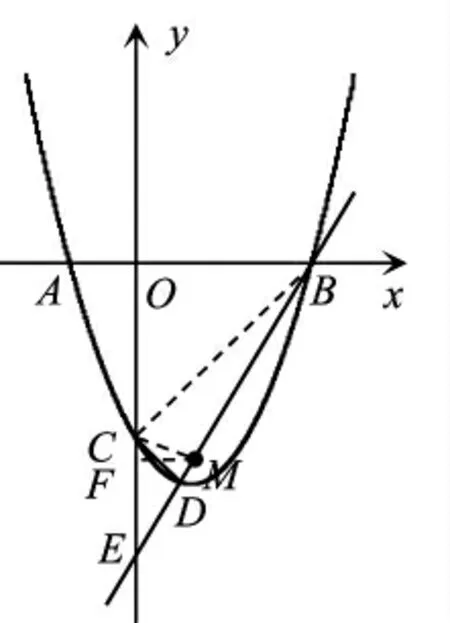
二、等腰三角形奠基,构造二倍角


三、等价转化,探寻特殊角

