应用深度强化学习的压边力优化控制

2020-06-24张新艳余建波

哈尔滨工业大学学报 2020年7期

张新艳，郭鹏，余建波

(同济大学机械与能源工程学院, 上海 201804)

板材拉深成形作为一种基础零部件制造工艺，被广泛应用于汽车、机电、轻工和航空航天等诸多领域. 拉深成形通过压边力(blank holder force，BHF)来控制金属材料的流动，从而影响最终成品的成形质量. 在拉深过程中采用恒定的压边力容易导致起皱与破裂等质量缺陷，因此在拉深过程中合理地控制压边力参数就成为防止起皱、破裂和提高成品质量的重要手段之一.

在压边力控制领域，最优化理论与有限元模拟相结合是一类常用的方法. Ghouati等[1]提出了网格法与单纯形法相结合的优化方法，其计算效率高，能够有效减少有限元仿真次数，但无法保证所求的解在可行域内. 包友霞等[2]在Ghouati提出的优化方法的基础上进行改进，使得优化过程中各变量点始终保持在可行域内，保证了解的可行性. 孙成智等[3]提出了一种集成了有限元模拟与自适应响应面法(adaptive response surface method，ARSM)的优化设计方法，并且应用信赖域模型管理来调节设计空间的变化，保证优化过程的收敛. Hillmann等[4]将成形极限图上各点到成形极限和起皱极限距离的加权和作为目标函数，以压边力作为设计变量，在有限元仿真环境下采用BFGS优化方法对压边力进行优化. Scott等[5]以极限应变作为目标函数，以压边力作为设计变量，在ABAQUS仿真环境下利用灵敏度分析方法对盒形件进行优化. 以上方法准确性较高，但数值模拟速度无法满足优化迭代要求，限制了方法的使用，并且最佳压边力搜索方向也难以确定.

神经网络被广泛应用于处理压边力控制问题中的非线性关系. Senn等[6]采用近似动态规划方法来进行压边力控制，利用神经网络来拟合系统动力学以及价值函数. 黄玉萍等[7]通过建立径向基网络，以应力、应变和减薄率作为输入，压边力曲线作为输出，构建了压边力优化模型. Qian等[8]和Manabe等[9]利用神经网络进行材料参数和工艺参数的在线识别，并结合弹塑性理论预测压边力大小. 汪锐等[10]通过将模糊控制技术与神经网络相结合，构建模糊神经网络专家系统来进行压边力的智能控制.

传统的压边力控制方法往往需要对拉深过程进行建模或依赖一些先验知识. Dornheim等[11]提出了一种无模型的压边力控制方法，避免了系统模型的拟合. 该方法将神经拟合Q迭代(neural fittedQiteration, NFQ)算法与有限元仿真相结合，为每个控制步长建立一个Q值网络. 然而NFQ是一种基于价值的强化学习算法，只能用于离散动作空间的控制问题，无法用于连续动作空间的控制问题. 综合以上分析，目前压边力控制领域还存在难以获得精确动力学模型以及压边力控制效果无法达到最优化的问题.

本文提出了一种基于深度强化学习的压边力优化控制模型，提高了压边力的控制效果；引入一种新的策略网络结构，进一步提高了深度强化学习在压边力控制任务中的控制效果；将压边力理论知识引入网络训练中，用理论压边力公式进行回放经验池的初始化，提高了压边力策略的学习效率；以一个圆筒件的拉深成形过程为分析对象，通过有限元仿真验证了本文提出的压边力优化控制模型的有效性.

1 理论背景

1.1 马尔科夫决策过程

强化学习(reinforcement learning，RL)问题一般由马尔科夫决策过程(Markov decision process，MDP)进行建模[12]. 通常将MDP定义成一个四元组(S,A,r,p)，其中：1)S为所有系统状态集合，st∈S表示智能体(agent)在时刻t的系统状态；2)A为动作集合，at∈A表示agent在时刻t所采取的动作；3)r为回报函数，r(st,at)表示在状态st下采取动作at后的奖励值；4)p为状态转移概率分布函数.p(st+1|st,at)表示在状态st下采取动作at后转移到下一状态st+1的概率.

在强化学习中，定义策略π：S→A为状态空间到动作空间的一个映射. 在每个离散步长t，agent在当前状态st下根据策略π采取动作at，接收到回报值r(st,at)并转移到下一状态st+1. 定义Rt为从t时刻开始到T时刻情节(episode)结束时的累积回报值：

式中：γ∈[0,1]为折扣率，用来确定短期回报的优先程度.

1.2 强化学习

强化学习的目标是寻找到一个最优策略πφ(参数为φ)来最大化期望回报值J(φ)=Esi～pπ,ai～π[R0][13]. 在行动者-评论家(actor-critic)框架中，策略网络(actor)通过确定性策略梯度[14](deterministic policy gradient，DPG)进行网络更新：

φJ(φ)=Es～pπ[aQπ(s,a)|a=π(s)φπφ(s)],

式中：Qπ(s,a)=Esi～pπ,ai～π[Rt|s,a]为动作值函数(critic)，表示在遵循策略π情况下，在状态s采取动作a后的期望回报值.

Q学习(Q-learning)使用时间差分算法进行动作值函数的学习，通过迭代贝尔曼方程求解Q函数：

Qπ(st,at)=r(st,at)+γEst+1,at+1[Qπ(st+1,at+1)],at+1～π(st+1).

对于巨大的状态空间，通常使用一个可微的函数近似器Qθ(s,a)估计动作值，其参数为θ. 深度Q学习[15](DeepQ-learning，DQN)算法采用了“目标网络”技术，在更新过程中使用另一个网络Qθ′(s,a)计算目标值：

yt=r(st,at)+γQθ′(st+1,at+1),at+1～πφ′(st+1).

式中动作at+1根据目标策略网络πφ′进行选择. 获得目标值后，DQN通过最小化损失函数L(θ)进行动作值网络参数的更新：

L(θ)=Est,at,r(st,at),st+1[(yt-Qθ(st,at))2].

2 基于深度强化学习的压边力控制策略优化算法

通过将双延迟深度确定性策略梯度[16](twin delayed deep deterministic policy gradient，TD3)与结构化控制网络[17](structured control network，SCN)相结合，本文提出了SCN-TD3算法用于压边力控制策略的学习.

2.1 双延迟深度确定性策略梯度

TD3是一种actor-critic框架的深度强化学习算法，在深度确定性策略梯度[18](deep deterministic policy gradient，DDPG)的基础上拓展而来. 为了解决actor-critic框架算法中的Q值过估计问题，TD3采用3个关键技术提高算法的稳定性和性能.

1)actor-critic框架下的剪裁双Q学习.受深度双Q学习[19](double deepQ-learning，DDQN)启发，TD3使用当前actor网络选择最优动作，使用目标critic网络评估策略：

yt=r(st,at)+γQθ′(st+1,πφ(st+1)).

在actor-critic框架中，目标actor与目标critic网络采用的“软更新”[18]方式使得当前网络与目标网络过于相似，无法有效分离动作选择与策略评估. 因此，算法保持了一对actor网络(πφ1，πφ2)和一对critic网络(Qθ1，Qθ2). 其中，πφ1根据Qθ1进行优化，πφ2根据Qθ2进行优化：

(1)

如果critic网络Qθ1与Qθ2相互独立，那么根据式(1)能有效避免由于策略更新所导致的偏差. 然而Qθ1与Qθ2在计算目标值时互相使用，并且基于相同的回放经验进行更新，因此两者并不互相独立. 为了进一步减小偏差，TD3使用了剪裁双Q学习(Clipped DoubleQ-learning)算法计算目标值：

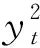
2)策略延迟更新.在深度强化学习算法中，目标网络被用于提供一个稳定学习目标. 通过多步更新，critic网络能逐渐减小与目标Q值之间的误差;然而,在critic网络高误差情况下,进行actor网络的更新会导致策略的离散行为. 因此,actor网络的更新频率应低于critic网络的更新频率，保证actor网络能在Q值误差较低的情况下进行更新，提高actor网络的更新效率. TD3在critic网络每进行d次更新后，进行一次actor网络的更新.

3)目标策略平滑正则化.由于TD3中采用的是确定性策略，进行critic更新时目标值很容易受函数近似误差的影响，导致目标值不准确. 因此TD3引入了一个正则化方法来减少目标值的方差，通过自举相似状态动作对的估计值进行Q值估计平滑化：

yt=r(st,at)+Εε[Qθ′(st+1,πφ′(st+1)+ε)].

TD3通过向目标策略添加一个随机噪声，并且在mini-batches上取平均的方法实现平滑正则化：

ε～clip(N(0,σ),-c,c).

2.2 结构化控制网络

受传统非线性控制理论启发，文献[17]提出了结构化控制网络(structured control network，SCN),将actor-critic框架中的策略网络分为非线性部分与线性部分两个部分. 将上述两个部分的动作值相加得到最终动作：

πφ(s)=πn(s)+πl(s).

式中:线性项πl(s)=K·s+b，K与b为线性控制增益矩阵与偏置项. 非线性项πn(s)为一个全连接多层神经网络，并去除输出层的偏置项. 这种简单的结构变化能够有效地提升深度强化学习的性能，在机器人控制以及视频游戏等领域均取得了比原网络结构更加优异的表现.

2.3 理论压边力知识

在压边力控制领域，研究人员通过板材成形理论以及对拉深过程的简化假设，推导了圆筒件拉深过程的有效压边力区间. 通过预先确定有效压边力区间，能够得到相对合理的压边力曲线.

如图1所示，板材拉深过程的有效压边力范围由上限压边力Qrup与下限压边力Qfwr组成.Qrup表示在拉深过程中保证工件不产生破裂缺陷的最大压边力,Qfwr表示在拉深过程中保证工件法兰边不产生起皱缺陷的最小压边力. 其中，

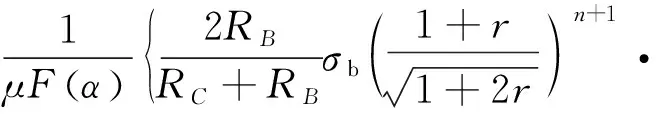
[1-μK1(α)]-2ωI(α)-J(α)}.

式中:μ为拉深过程中毛坯与模具间的摩擦因数，n为材料的硬化指数，σb为材料的抗拉强度，r为材料的厚向异性系数.RB、RC、F(α)、K1(α)、ω、I(α)与J(α)是随着拉深过程变化的变量，具体物理意义与计算方式参见文献[20].

式中:t0为板材厚度，B为材料的强度系数，y0为单波的最大挠度，r0为法兰内半径，m为拉深系数，F(n,m,ρ)与Fm(λm)为随拉深过程变化的两个变量，具体物理意义与计算方式参见文献[21].

图1中位于上限压边力与下限压边力之间的3条压边力曲线是由3种深度强化学习算法优化学习得到的. 可以看出，它们在整个拉深过程中始终保持在Qrup与Qfwr之间，保证了最终成品不产生质量缺陷.

图1 有效压边力Fig.1 Effective blank holder force

2.4 算法描述

本文将SCN-TD3与有限元仿真相结合，构建了基于深度强化学习的压边力控制策略优化算法, 算法描述如下.

输入：有限元模型

输出：actor网络πφ

第1步：初始化critic网络Qθ1与Qθ2的参数θ1与θ2，以及actor网络的参数φ

第2步：初始化目标网络参数：θ1′←θ1，θ2′←θ2，φ′←φ

第3步：初始化回放经验B

第4步：For episode = 1,Mdo

第5步：初始化有限元模型状态s1

第6步：Fort= 1,Tdo

第7步：选择动作at，

at←πφ(st)+ε,ε～N(0,σ)

第8步：在有限元模型中执行at，输出st+1与rt

第9步：将转移经验存储到回放经验中，(st,at,r(st,at),st+1)→B

第11步：利用目标网络得到动作

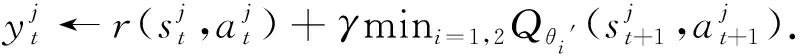
第13步：根据梯度

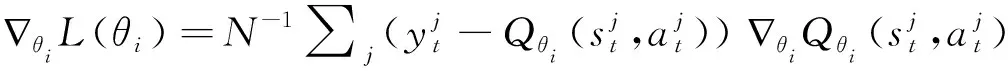
第14步：Iftmoddthen

第15步：根据梯度

第16步：更新目标网络

θi′←τθi+(1-τ)θi′，φ′←τφ+(1-τ)φ′

第17步：End if

第18步：End for

第19步：End for

3 基于深度强化学习的拉深控制模型

3.1 问题描述

本文针对板材拉深过程进行压边力控制优化，得到成形质量合格的成品件. 如图2所示，板材拉深装置主要由毛坯、冲头、压边圈和凹模4部分组成. 毛坯被放置在压边圈与凹模法兰之间，由压边圈夹紧. 整个加工过程被分为5个控制步长，每个控制步长内压边力的大小相等，冲头以恒定速度向下冲压，将毛坯压入凹模腔体. 本文将板材拉深控制过程建模成离散时间的马尔科夫决策过程，以板材内部的Mises应力分布作为系统状态s，每个控制步长内的压边力大小作为系统动作a. 由于本文所建立的有限元模型被划分为527个单元，使用全体单元的Mises应力分布作为系统状态会使得状态空间过于庞大，不利于问题的有效求解. 因此，本文采用图2标记的部分有限元的Mises应力作为系统状态，在反应系统状态特征的同时将系统状态缩小为27维.

图2 拉深模型Fig.2 Deep drawing finite element model

3.2 压边力控制模型

压边力控制模型如图3所示，主要由环境与智能体两部分组成. 其中，环境由有限元模型与成本函数组成；智能体由两个价值网络以及一个策略网络组成. 环境接受到动作a，根据前一时刻环境状态得到当前的回报r与观察值s并将其输入智能体，智能体输出下一步长动作，开始下一次交互. 智能体在与环境进行交互的过程中利用深度强化学习算法不断地更新网络参数，最终学习到一个最优的压边力控制策略.

图3 压边力控制模型Fig.3 Blank holder force control model

3.2.1 有限元模型

本文建立的板材拉深仿真模型如图4所示. 通过假设模型对称性与材料各向同性，建立了1/4的板材拉深三维模型，并将拉深过程划分为6个离散的时间步长. 其中前5个为控制步长，完成向下拉深过程，最后1个步长为卸载步长，冲头恢复到原始位置同时将压边力卸载. 模型根据上一步长的状态与输入的压边力值，计算出下一步长的状态.

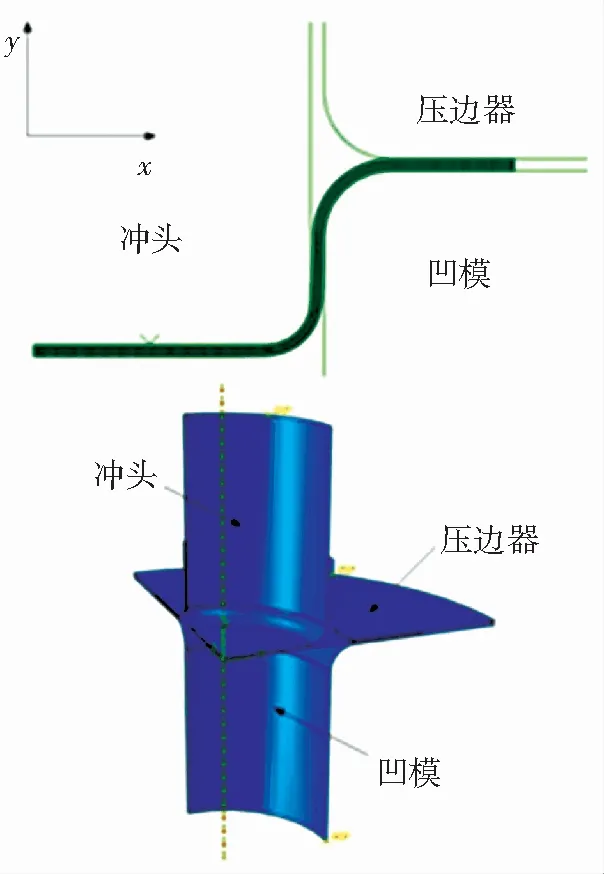
图4 有限元模型Fig.4 Finite element model

有限元模型由3个刚体部件与1个可变形毛坯组成. 刚体部件分别为冲头、凹模和压边圈. 冲头半径Rp为25 mm，冲头圆角半径rp为4 mm，凹模内径Rd为26.2 mm，凹模圆角半径rd为6 mm. 圆形毛坯厚度H为1 mm，半径R0为50 mm. 毛坯材料属性为弹塑性材料，材料为08F低碳钢[22]. 材料的弹性模型为线弹性模型，塑性模型为符合Mises屈服准则的各向同性模型. 毛坯的有限元单元类型为可变形的4节点4边形壳单元(S4R).

冲头以恒定速度4 mm/s向下冲压，将毛坯压入凹模腔中，拉深深度S为20 mm. 压边力在每个控制步长开始时给出，在每个控制步长内压边力保持不变，均匀施加在压边圈上. 压边力变化范围为5 000～13 000 N.

本文用ABAQUS进行有限元模型的搭建. 在线优化控制环境中，智能体基于当前得到的系统状态来设置动作. 为了符合在线优化控制环境的要求，保证有限元模型的有效性与可重用性，使用了ABAQUS脚本与分析重启动技术.

3.2.2 回报函数

回报函数仅由终止状态产生的回报值组成. 控制目标为生产出的工件内部应力低,材料厚度充足,并且材料利用率低. 针对以上3个目标，分别建立评价指标函数并通过三者的加权和得出总的质量评价函数[11].

有限元模型由527个单元组成. 根据有限元仿真输出的Mises应力分布云图、厚度分布云图与U1位移分布云图，可以得到最终成品每个单元的Mises应力值mi(i=1,2,...,527)、单元厚度hi(i=1,2,...,527)以及毛坯边在x轴方向上的位移d. 根据以上的数据，建立成本函数：

Cb(sT)=-minhi，

Cc(sT)=-d.

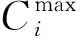
最后，本文以加权调和平均的形式给出总的质量评价函数：

式中权重值wi用于控制各个成本项的重要性，本文中权重wi均为1.

4 实验与结果分析

受硬件因素影响，实际实验验证十分困难. 本文参考文献[11]的压边力控制仿真实验设计，利用圆筒件拉深成形的有限元仿真进行实验.

4.1 训练过程分析

在SCN-TD3中，策略网络与价值网络的结构均为4层神经网络，隐藏层节点为300. DDPG与TD3的网络结构与SCN-TD3一致. SCN-TD3算法中，学习率为0.000 1，探索率σ为0.1，目标动作噪声方差σ'为0.2，目标动作截断值c为0.2，策略网络更新间隔d为2. DDPG和TD3的参数与SCN-TD3一致. 训练过程中，算法在每个训练步长进行10次网络更新.

图5为不同算法回报值随训练步长数的变化情况. 本文将各控制步长下压边力的相邻训练步长的差作为算法收敛的判断依据. 当连续100个训练步长下，各压边力相邻训练步长的差均<1 000 N时，认为算法收敛. 在SCN-TD3控制下，回报值大约在第1 500个步长收敛，而在DDPG与TD3控制下，回报值大约在第1 800与第1 700个步长收敛. 从回报值的整体变化趋势上看，SCN-TD3控制下的回报值收敛最快，并且最终收敛到的回报值水平高于TD3. TD3控制下的回报值收敛略快于DDPG，并且最终收敛到的回报值水平高于DDPG. 这主要是由于1)TD3算法中采用的剪裁双Q学习、延迟策略更新和目标策略平滑正则化这3种技术，有效地缓解了价值网络的过估计问题以及过估计问题给策略网络更新所带来的影响; 2)策略网络的非线性结构与线性结构能够同时结合全局控制与局部控制的优点. 各算法的优势对比如表1所示.

图5 回报值随训练步长变化Fig.5 Variation of episode reward with step

表1 算法优势对比Tab.1 Comparison of different algorithms

在训练过程中，每5个训练episode结束后，利用当前的策略网络进行10次拉深仿真控制，取平均值作为验证回报值. SCN-TD3得到的最优验证回报值为1.928 8，而DDPG与TD3控制下的最优验证回报值分别为1.602 9与1.690 8. 各算法最优验证回报值所对应的压边力控制策略如表2所示.

表2 最优控制策略Tab.2 Optimal control policy N

4.2 训练过程压边力变化分析

为了探究压边力在训练过程中的变化情况，本文给出了DDPG、TD3与SCN-TD3控制下各控制步长的压边力随训练步长的变化情况(见图6). 由图6可知，在训练的早期,步长2到步长5的压边力聚集在最小值5 000附近，3种算法均陷入局部最优. 随着训练的进行，算法逐渐跳出局部最优点，最终收敛于一定的压边力水平. SCN-TD3控制下各步长压边力收敛速度均快于其他两者，体现了SCN-TD3在性能上的优势.

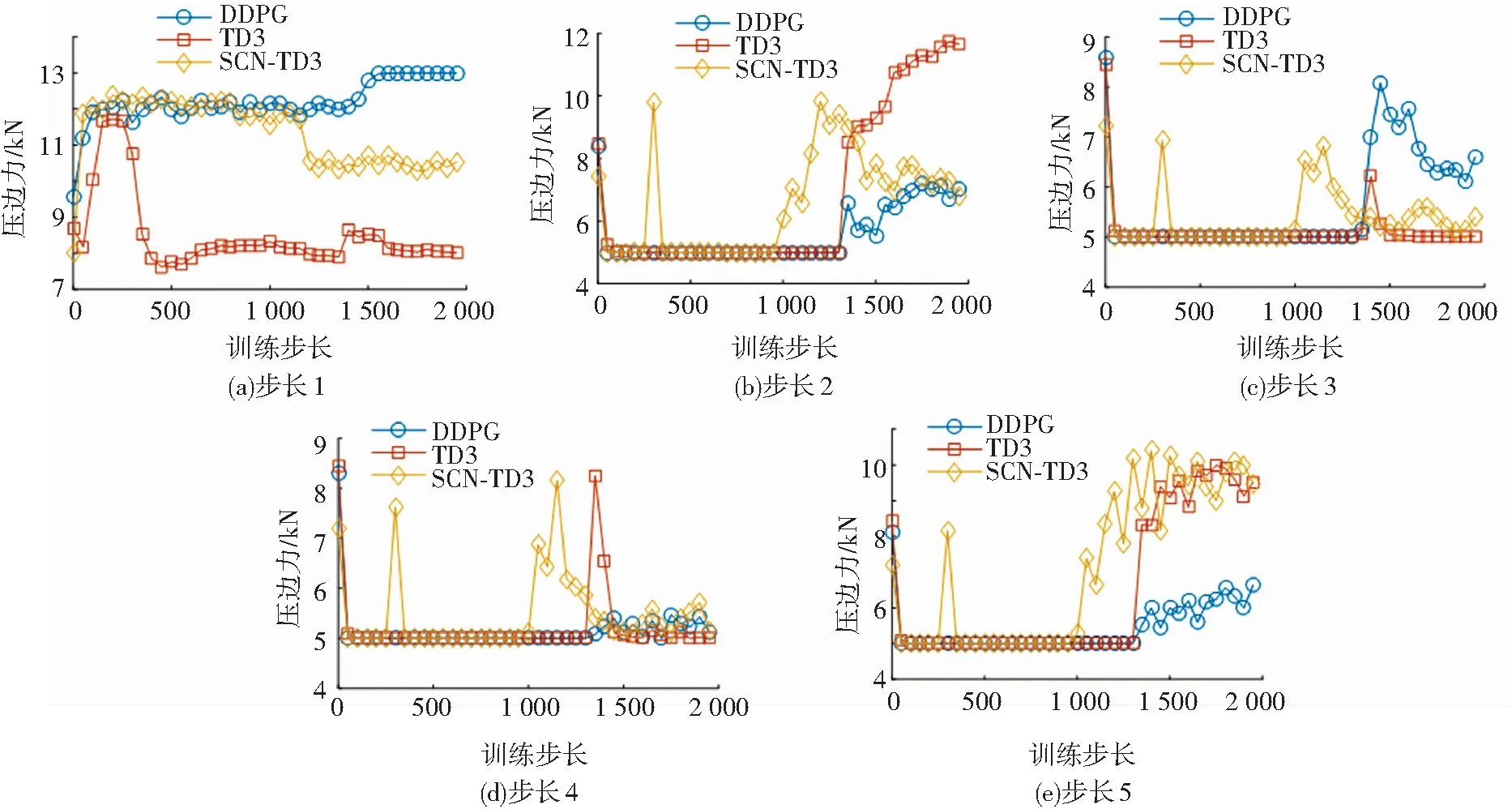
图6 各控制步长压边力变化Fig.6 Variation of blank holder force with each control step

4.3 成品质量分析

根据DDPG、TD3以及SCN-TD3学习到的最优压边力控制策略，在ABAQUS中分别进行板材仿真拉深. 根据仿真结果输出的Mises应力分布云图、厚度分布云图与U1位移分布云图，进行成品质量分析. Mises应力分布云图展示了成品各有限元单元的Mises应力分布情况. 根据图7～9，可以得到三者的内部应力项指标分别为4 221、4 475以及3 708. 从总体分布上看，TD3控制下的成品的内部应力和最小，DDPG控制下的成品的内部应力和最大.

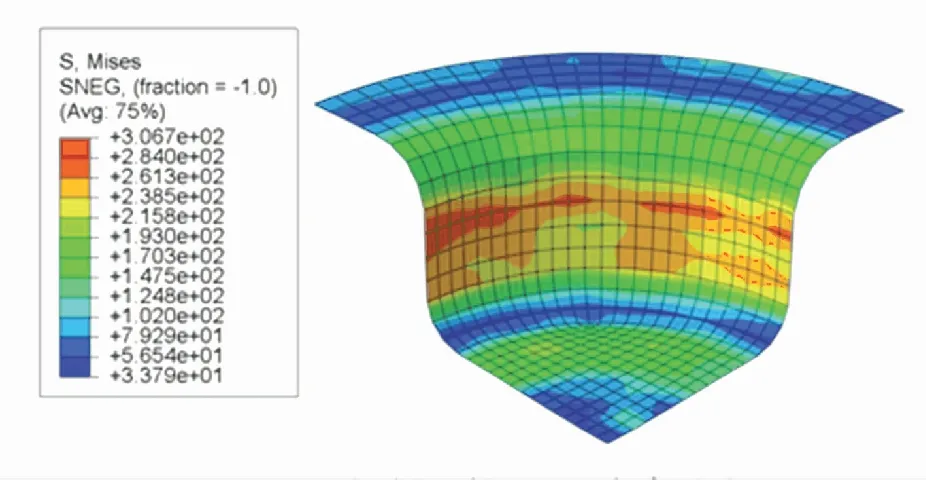
图7 SCN-TD3控制下的Mises应力分布云图Fig.7 Mises stress distribution under SCN-TD3

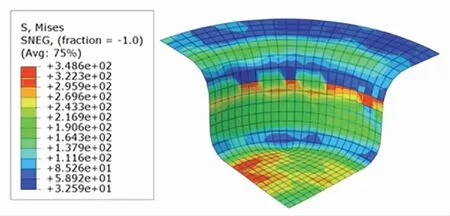
图8 DDPG控制下的Mises应力分布云图Fig.8 Mises stress distribution under DDPG

图9 TD3控制下的Mises应力分布云图Fig.9 Mises stress distribution under TD3

厚度分布云图体现了成品各处厚度的分布情况. 根据图10～12，SCN-TD3控制下成品的最小厚度为0.858 4 mm，DDPG控制下成品的最小厚度为0.853 3 mm，TD3控制下成品的最小厚度为0.850 3 mm. SCN-TD3控制下的成品厚度最为充足，TD3控制下的成品厚度最薄.

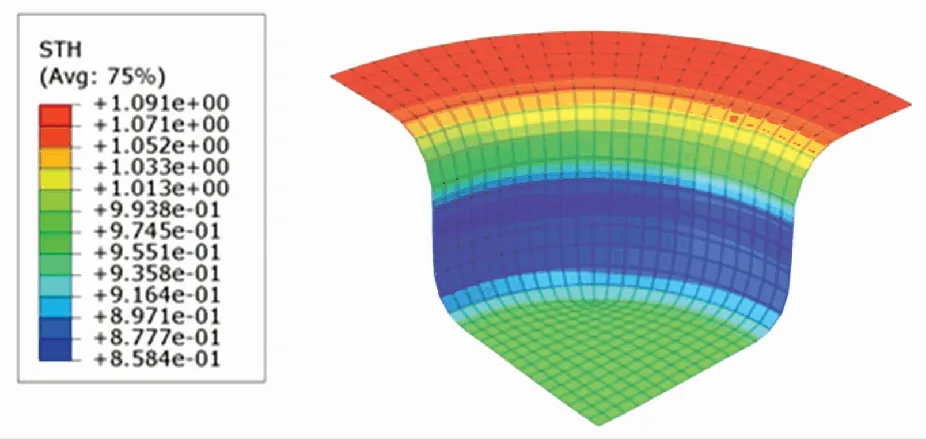
图10 SCN-TD3控制下的厚度分布云图Fig.10 Thickness distribution under SCN-TD3

U1位移分布云图表示成品的每个有限元单元在x轴向上的位移. 根据图13～15可知，SCN-TD3控制下成品的法兰边位移为7.781 7 mm，DDPG控制下成品的法兰边位移为8.0837 mm，TD3控制下成品的法兰边位移为7.944 6 mm. 表明SCN-TD3控制下的材料消耗比DDPG与TD3都要小.

图11 DDPG控制下的厚度分布云图Fig.11 Thickness distribution under DDPG

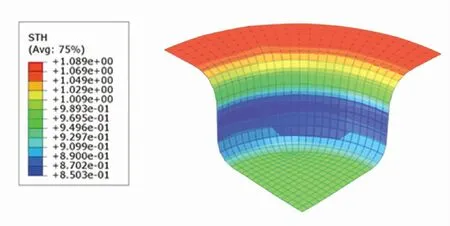
图12 TD3控制下的厚度分布云图Fig.12 Thickness distribution under TD3

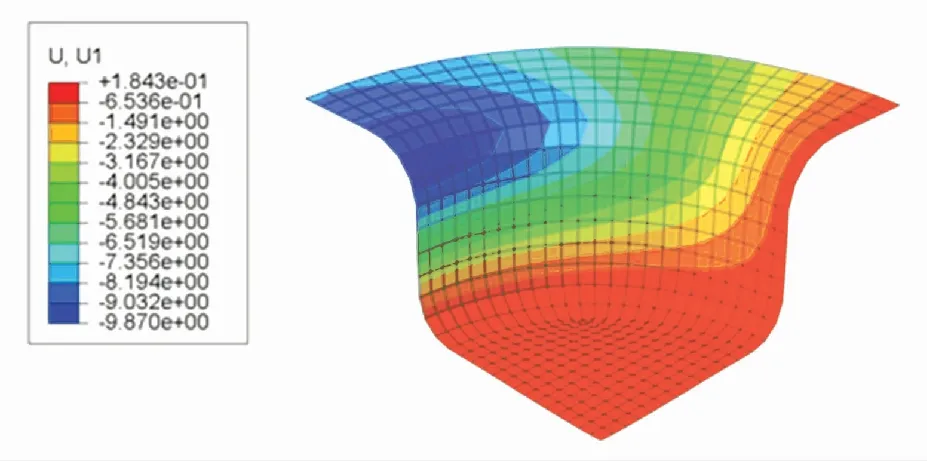
图14 DDPG控制下的U1位移分布云图Fig.14 U1 displacement distribution under DDPG

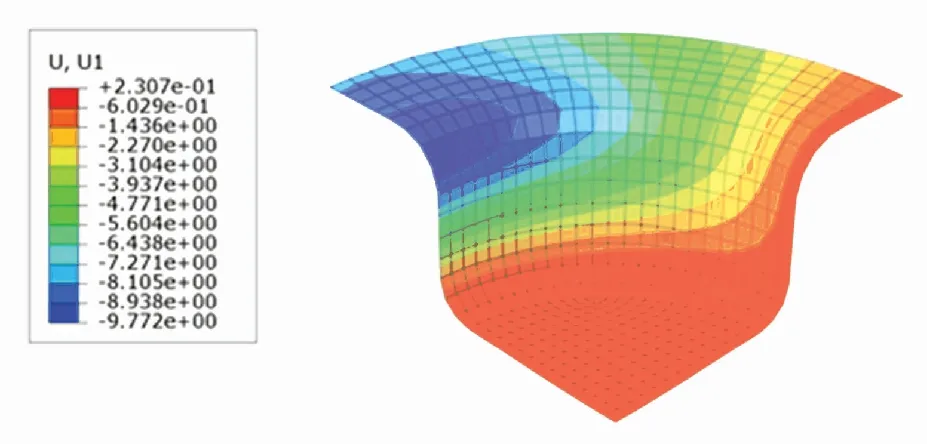
图15 TD3控制下的U1位移分布云图Fig.15 U1 displacement distribution under TD3

由于成本函数的组成为内部应力项、最小厚度项与材料消耗项的调和平均，因此尽管SCN-TD3在内部应力和指标上的表现不如TD3，但是其在3个成本项中的综合表现最优. 综合以上分析可知，相较于DDPG与TD3，SCN-TD3控制下成品的内部应力和较小，材料最小厚度充足，材料消耗程度最低，总体质量最优.

4.4 理论知识对于训练过程的影响

根据图1的理论有效压边力区间产生多条可行的压边力轨迹以及转移经验. 将有效压边力产生的转移经验加入初始经验回放池，达到将理论知识引入压边力策略优化过程的目的.

通过对各控制步长所对应拉深行程下的有效压边力区间进行随机采样，得到了1 000条有效压边力轨迹及5 000个有效转移经验. 为了探究理论知识对于训练过程的影响，控制初始转移经验中有效压边力转移经验所占比例分别为0%、25%、50%、75%和100%，输出所对应的回报值随训练步长的变化情况，如图16所示.

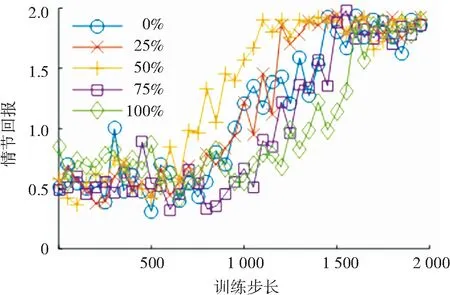
图16 不同比例有效转移经验下的回报值变化

Fig.16 Variation of episode reward with different percentages of efficient transition experience

由图16可知，随着有效转移经验所占比例的增加，训练过程中回报值的收敛越来越迅速，在50%达到最快收敛速度，随后收敛速度随有效转移经验所占比例的增加开始下降. 这表明，在初始经验回放中添加适量的有效转移经验能够为网络的训练提供一个良好的初始训练数据，让策略网络的参数更快地往回报值高的参数空间进行梯度下降. 然而当初始回放经验中的有效转移经验过多时，由于缺少低回报值的转移经验，策略网络的更新无法有效地远离低回报值的参数空间，反而使得回报值收敛速度下降. 根据以上分析可知，在初始经验回放池中保持经验样本的多样性有助于策略网络的训练.