基于RTU的PMSM无位置传感器低速控制算法研究

2020-06-24温志威石懿晨杨泽贤陈瑜涵朱雨菲

电动工具 2020年3期

温志威，石懿晨，杨泽贤，陈瑜涵，朱雨菲

( 南通大学电气工程学院，江苏南通 226019 ）

0 引言

永磁同步电机因具有体积小、效率高、启动转矩较大、功耗低等诸多特点，在交通运输以及工业传动上应用广泛[1-2]。传统的闭环控制方式利用安装在转轴上的旋转编码器获取转子位置及转速，但编码器的安装降低了系统的稳定性及可靠性且增加了系统的维护成本[3]。因此近年来永磁同步电机的无位置控制成为研究的热点[4]。无位置控制主要基于滑膜观测器、模型参考自适应、拓展卡尔曼滤波等方法来获取转子位置信息。文献[5-6]采用滑膜观测器估算转子位置信息，该方法计算简单，动态响应快，但误差较大，存在抖振问题。文献[7]采用卡尔曼滤波估算转子位置信息，该方法计算复杂，难以得到普及，存在着低速状态下跟踪效果相对较差，响应时间长的缺点。文献[8-9]中采用模型参考自适应估算转子位置信息，该方法具有鲁棒性强，控制精度高，但在低速时抖振较大，控制效果不明显。由此可知，上述方法在无位置传感器低速控制中效果不理想。文献[10-13]采用高频信号注入法来实现对电机无位置传感器低速控制，具有良好的动稳态性能，能够有效估计转子位置以及转速。

本文基于RTU 半实物仿真平台，搭建基于脉振高频信号注入法的无位置传感器控制系统，通过实验证明该控制策略在低速范围内的可靠性和有效性以及RTU 平台的可行性。

1 永磁同步电机数学模型

将PMSM 在三相静止坐标系下的数学模型经Clarke 变换及Park 变换后可得到PMSM 在dq 旋转坐标系下定子电压的数学模型方程为：

式中：ud,uq分别为dq 轴的定子电压；id,iq分别为dq 轴的定子电流；Rs为电机绕组；Ld,Lq分别是dq 轴的定子电感；φf为永磁体磁链。

电机的机械运动方程为：

式中：ωm为电机机械角速度；J 为转动惯量； B 为阻尼系数；TL为负载转矩；Te为电磁转矩。

电磁转矩方程为：

式中：pn为电机极对数。

2 脉振高频信号注入法

2.1 脉振高频电压激励下三相PMSM的电流响应

定义定子的转子误差角为：

永磁同步电机在高频信号激励下的数学模型可简化为阻抗模型：

此时高频响应电流可简化为：

2.2 转子位置估计方法

转子位置原理见图2。

如转子位置估算误差足够小，可将该信号线性化，即

2.3 基于PLL的转子位置估计方法

为了获得电机的转子位置角，采样PI 调节器构成的PLL 系统，其控制框图如图3 所示。

3 半实物仿真平台

3.1 基于Rtuint平台介绍

实时数字控制系统RTU-BOX 由硬件控制器、底层驱动软件包RTU-BOX.Lib、集成开发环境Rtunit Studio、Simulink®模型库RtunitToolbox 和实时代码生成组件RTU-Coder组成，如图4 所示。

RTU-BOX 的硬件控制器采用多核异构技术，处理器由DSP、ARM 和多个FPGA 组成，性能稳定、功能丰富。主处理器采用了TI 公司Delfino 平台的32 位浮点型数字信号处理器TMS320C28346，主频为300MHz。

3.2 实验硬件系统

永磁同步电机无位置传感器低速控制实验平台系统由实时数字控制系统RTU-BOX、基于拓扑的模块化逆变器RTCON-103P、PMSM组成，其系统结构框如图5 所示。

3.3 实验软件系统

采用RTU 强大的软硬件系统研究新的控制算法时，通常需要四步骤：

1）确定控制算法；

2）使用Matlab/Simulink 建立系统仿真模型，验证算法的正确性与可行性；

3）将模型转换为基于RTU 的仿真模型并生成代码；

4）将代码下载入系统，在线调试参数，完成算法的验证。如图6 所示。

4 仿真实验

为验证所提出的基于RTU 的PMSM 无位置传感器低速控制算法的研究，本文结合如图7 所示的无位置传感器控制框图，在RTU 实验平台中进行实验。如图7 所示，控制系统由坐标变换模块、PI 模块、SVPWM 模块、永磁同步电机模块、逆变器模块等组成。根据文献[17]高频信号注入观测器中Kp 和Ki 取值分别为120 和0.5。

仿真与实验中永磁同步电机参数如表1 所示：

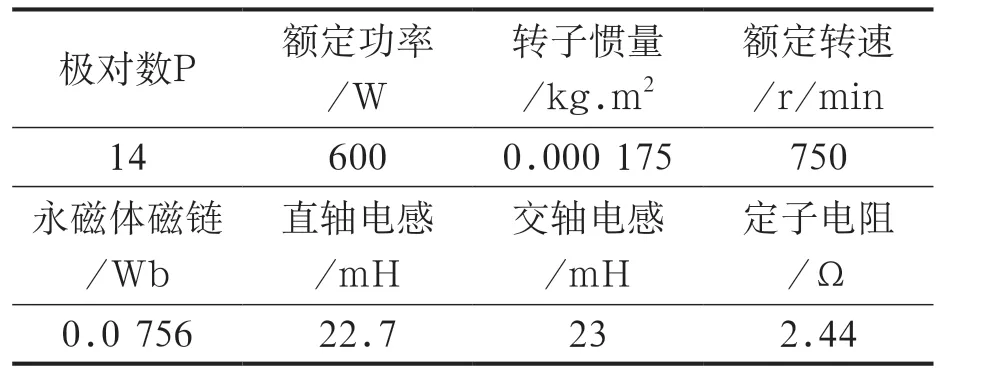
表1 永磁同步电机参数

为了验证脉振高频信号注入法在实际系统中的的有效性，搭建了基于RTU 的PMSM 无位置传感器控制系统的实验平台。如图8 所示，实验平台包括直流电源、示波器、驱动器、转接板、上位机等。

如图9 在空载情况下，给定速度为20 r/min 时，估计转速和实际转速误差较小，数值在零附近波动。转子估算位置误差约为2.1 rad，整体来看，速度和位置误差都在可接受的范围内。

为了验证脉振高频信号注入法对速度突变的响应能力，实验从20 r/min 切换至70 r/min，其速度波形如图10 所示。切换过程中，转速在很短时间（小于0.2 s）内收敛至70 r/min，误差基本为零；在70 r/min 时转子的位置误差约为1.85 rad，表明该方法在较宽的速度范围内有良好的估算效果。