考虑失效模式相关性的传动齿轮可靠性分析
2020-06-23郭正阳李永华
郭正阳,宫 琦,李永华
(大连交通大学 机车车辆工程学院,辽宁 大连 116028)
0 引言
传动齿轮可靠度是保障机器安全运行的关键[1]。随着工作时长的增加,齿轮会发生各种失效,齿轮的破坏往往是由多种模式同时发生导致的,可见失效模式间并非相互独立的,而是具有某种相关性。唐家银等[2]提出齿轮失效模式间具有关联性,在进行齿轮研究时应将此关联性考虑在内;白恩军等[3]以齿根弯曲和齿面接触的静强度失效为出发点,提出一种失效模式相关的可靠性评估方法;安宗文等[4]考虑相关性的影响建立了齿轮可靠性模型,研究结果验证了该可靠性模型的正确性和高效性;张道兵等[5]建立了拥有多极限状态方程的可靠性模型,并利用该模型计算多失效模式相关的结构可靠度;韩文钦等[6]利用鞍点逼近法及Copula函数求得多失效模式功能函数的概率分布。本文以动车组传动齿轮为研究对象,综合考虑各失效模式相关性,对传动齿轮进行可靠度和灵敏度分析,最终结果可为齿轮设计和优化提供理论参考。
1 可靠性建模
传动齿轮的齿面接触疲劳强度为:
(1)
其中:ZH为节点区域系数;ZE为弹性系数;Zε为重合度系数;Ft为分度圆上的圆周力;d1为分度圆直径;b为齿宽;u为传动比;KA为使用系数;KV为动载系数;KHβ为接触强度的齿向载荷分布系数;KHα为接触强度的齿间载荷分配系数。
接触疲劳强度极限为:
σHS=σHlimZNZLZVZRZWZX.
(2)
其中:σHlim为接触疲劳极限;ZN为寿命系数;ZL为润滑剂系数;ZV为速度系数;ZR为齿面粗糙度系数;ZW为硬化系数;ZX为尺寸系数。
齿根弯曲疲劳强度为:
(3)
其中:mn为齿轮的法向模数;YFa为齿形系数;Ysa为应力修正系数;Yε为重合度系数;Yβ为螺旋角系数;KFβ为弯曲强度的齿向载荷分布系数;KFα为弯曲强度的齿间载荷分配系数。
齿根弯曲疲劳强度极限为:
σFS=σFlimYSTYNTYδrelTYRrelTYX.
(4)
其中:σFlim为弯曲疲劳极限;YST为应力修正系数;YNT为寿命系数;YδrelT为敏感系数;YRrelT为表面状况系数;YX为尺寸系数。
传动齿轮的积分温度为:
(5)
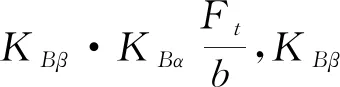
极限积分温度为:
θsint=θMT+C2XWθflaintT.
(6)
其中:θMT为齿轮温度;XW为焊合系数;θflaintT为平均温升。
根据应力-强度干涉理论,构建齿面接触疲劳、齿根弯曲疲劳以及齿面胶合三种失效模式的结构功能函数如下:
(7)
其中:gi(x)为结构功能函数;Ri为广义强度;Si为广义应力。
2 可靠性分析

(8)
Ri=Φ(βi)i=1,2,3.
(9)
其中:μZ、σZ和βi分别为各功能函数的均值、标准差及可靠性指标;Φ(*)为标准正态分布函数。
考虑失效模式相关性对传动齿轮系统可靠度的影响,利用相关系数矩阵表征失效模式间的相关性。相关系数表达式为:
(10)
其中:Cov(gi(x),gj(x))为gi(x)与gj(x)的协方差;D[gi(x)]为gi(x)的方差;D[gj(x)]为gj(x)的方差。
基于式(8)和式(10),应用MATLAB软件中的mvncdf函数可得到任意两种失效模式相关下的传动齿轮系统可靠度:
R=mvncdf(β,0,ρ).
(11)
其中:β为可靠度指标;ρ为相关系数;mvncdf为联合概率密度函数。
3 灵敏度分析
为提高齿轮传动系统可靠度,本文开展失效模式和随机变量两种灵敏度分析。其中失效模式对失效概率的灵敏度为:
(12)
其中:∂Pf/∂Pfi为失效模式灵敏度;Pf为齿轮传动系统失效概率;Pfi为各失效模式的失效概率;normcdf为累计正态分布函数的反函数。
随机变量对失效概率的灵敏度为:
(13)
(14)

4 工程案例
以某动车组传动齿轮为例,进行考虑失效模式相关性的可靠度研究,该传动齿轮几何参数见表1。利用ANSYS对上述三个结构功能函数分别抽样1 000 000次,得到三种失效模式的失效概率分布,如图1所示。

表1 动车驱动装置传动齿轮几何参数

图1 各失效模式的概率分布
由图1可知,各失效模式功能函数均服从正态分布,特征值见表2。

表2 失效模式特征值
由式(10)得到失效模式相关系数见表3。由表3可知,齿面接触疲劳和齿根弯曲疲劳相关性最大,齿根弯曲疲劳与齿面胶合相关性最小。
利用式(11)求得传动齿轮考虑失效模式相关性的可靠度,并与Monte Carlo法模拟结果对比,见表4。在可靠度求解基础上,由式(12)~(14)得到各失效模式灵敏度,见表5,各随机变量灵敏度如图2、图3所示。

表3 各失效模式相关系数
表4对比结果验证了本文方法的正确性,且可知该方法精度较高。由表5可知,齿面接触疲劳对传动齿轮系统可靠度影响最大,其次是齿根弯曲疲劳,齿面胶合影响程度最小。

表4 失效相关的可靠度结果比较

表5 各失效模式灵敏度
由图2、图3可知:齿面接触疲劳失效模式中,随机变量的均值对系统可靠度影响最大,KHα和KHβ的方差对系统可靠度影响最大,其余变量的方差影响较小;齿根弯曲疲劳失效模式中,KV和KA的均值对系统可靠度影响较大,所有变量的方差与系统可靠度呈负相关;齿面胶合中,KA、KV和μm的均值以及μm的方差对系统可靠度影响较大,其余变量影响较小。
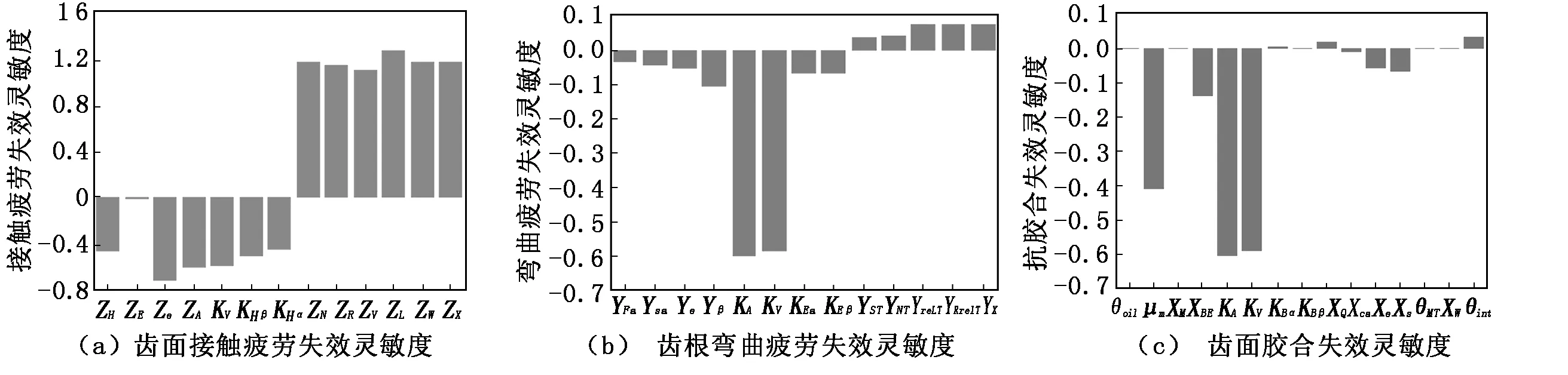
图2 均值灵敏度

图3 方差灵敏度
5 结论
(1) 提出一种考虑失效模式相关性的传动齿轮可靠性分析方法,以动车组传动齿轮为研究对象进行可靠性分析。研究表明动车组传动齿轮考虑失效模式相关性的可靠度指标为1.068 7,结果验证了该方法的正确性、可行性。
(2) 齿面接触疲劳及相关随机变量对传动齿轮系统可靠度影响最大,齿根弯曲疲劳和齿面胶合失效模式中的随机变量KA和μm的方差以及KA、KV的均值对传动齿轮系统可靠度影响较大。此分析结果可为传动齿轮的设计提供理论参考。
