降雨条件下坡长对黄土裸坡面径流流态的影响

陈彦平

(山西省水文水资源勘测局，山西 太原 030001)

坡面径流边界条件复杂多变，且水深通常只有几毫米[1]。水流流态作为表征坡面薄层水流动力学特性的基本参数，一直被视为坡面薄层水流特征值研究的热点问题，虽然近年来国内外学者采用变坡放水冲刷试验或人工模拟试验方法对水力学特征值进行了诸多研究，并取得了一定的成果[2- 6]，由于坡面微地貌分布不均[7]等原因，薄层水流在时间和空间上不断变化。因此，目前关于其流态的研究尚无定论，主要集中于两种结论:①层流;②紊流和过渡流的混合体。

潘成忠等[8]通过室内模拟试验研究指出坡面薄层径流属层流的缓流范畴，但雷诺数与佛汝德数均随着放水流量的增加而增大，径流虽处于层流状态但向急流变化[9]。Horton[10]认为坡面流属于完全的紊流中间点缀着层流，处于混合状态，是一种不同于普通的层流、紊流和过渡流的扰动流体[11]或由层流过渡到紊流[12]，黄土坡面薄层径流在时间和空间上分布不均匀且不稳定，属于过渡流或紊流范畴[13- 15]，而林地坡面流介于层流与紊流之间[16]。也有学者指出降雨情况下坡面薄层径流为伪层流，即既有紊流也有过渡流[17]，敬向峰等[18]将泥沙颗粒假定为球形，探讨利用绕流雷诺数判定坡面径流流态(临界值0.35-900)，并指出其为过渡流，但因试验条件等多种因素所限，结论并未被广泛应用。本文以具有代表性的离石黄土坡面(无植被生长)为试验区，基于人工模拟降雨试验手段，分析降雨与坡长对坡面薄层径流流态的影响，以期为该区坡面水土流失治理提供一定的科学依据。

1 模拟降雨试验

1.1 研究区概况

试验区位于晋西吕梁市王家沟流域，年降雨量极值间于240.2～711.5mm，多年平均值490.3mm，平均侵蚀模数7651t/km2。试验土壤采自王家沟流域坡面上，分层取土装袋运回实验室，按照野外原状土顺序分层装入土槽，装的过程中进行压实处理，土壤装好后静置至少一个月，并定期在上面洒水，以最大限度保证模拟野外原状土状态，测得土壤容重1.35g/cm3，有机质13.42g/kg，pH值8.15，土壤初始容积含水量13.99%，总孔隙度49.05%，土壤黏粒含量为1.75%，粉砂粒14.2%，砂粒84.05%。

1.2 模拟降雨装置与试验设计

模拟试验在室内进行，利用便携式人工模拟降雨器模拟天然降雨，通过对雨强多次标定，降雨均匀性可达85%以上，最大限度接近天然降雨状态。下垫面为5个并排放置的径流槽，槽长分别为1，2，3，4，5m，宽0.5m，坡度20°，表面为裸坡面。根据对王家沟多年降雨调研，设计雨强分别为30，60，80、125mm/h。为保持场降雨土壤前期含水率基本相同，每次试验前用铝盒采集坡面不同部位土壤测定水分含量，降雨试验开始后，用秒表记下初始产流时刻，之后，每隔2min用塑料瓶将含泥沙的径流采集起来，产流后继续降雨30min，每场降雨得到15个径流泥沙样，将其在实验室静置24h，测得径流体积后将上清液倒掉，置于105°C的烘箱中12h得到不同时间的产沙量。每个雨强重复两次试验，共获得8场降雨径流泥沙数据，取两次试验平均值作为最终数值。

2 结果与讨论

2.1 雨强与径流流态的关系

由于坡面薄层水流分布在时间和空间上的不稳定和不均匀性，导致目前尚无确定的方法与标准判定其流态，将坡面薄层水流视为二元明渠流，依据明渠水流判断标准，以500为界判别是否有紊流出现，雷诺数Re大于500时为紊流，等于500为过渡流，小于500时为层流。水流佛汝德数Fr大于1是急流，等于1是临界流，小于1为缓流。结果如图1所示，雨强30～125mm/h且坡长为1～5m条件下，坡面径流雷诺数均小于500，佛汝德数均大于1，则在该试验条件下坡面径流流态属于层流、急流范畴。同一坡长时，径流雷诺数随降雨强度增大而增加，雨强越大增速越快，坡长越长，雷诺数增加的幅度越大，而雷诺数随着雨强与坡长的变化没有明显规律。如坡长为1m，雨强从30mm/h增大到125mm/h时，坡面径流雷诺数在7.83～25.24内变化，增幅为17.41；坡长2、3、4、5m，雷诺数增幅分别为40.46、52.77、65.61、68.62。

图1 不同坡长下雷诺数、佛汝德数随雨强的变化

产生这种现象主要与土壤入渗性能、径流特性及雨滴特性有关。

(1)当降雨强度小于土壤入渗率时，降雨初期并没有明显径流，而是就地入渗，随着降雨的持续，形成的少量径流在向坡面下部流动时也会渗入土壤，当雨强增大到超过土壤入渗强度时形成径流沿坡面向下流动(即超渗产流)。而坡面逐渐产生的细沟使得面状漫流变成线状股流，增加径流深度与流动速度[19- 21]，从而增强坡面径流紊动性，以坡长2m为例，雨强由30mm/h增大到125mm/h时，测得坡面平均流速在0.078～0.140m/s范围内增加，平均径流深为0.152～0.413mm。

(2)试验过程中用滤纸色斑法测得雨强30～125mm/h时，雨滴直径随雨强的增大而增大，试验实测4个雨强下雨滴平均直径0.55、1.17、1.80、2.48mm，表明较大粒径的雨滴对坡面径流有较强的扰动。另外，坡面即使有径流覆盖，当具有较大动能的大直径雨滴降落到坡面时，其对土表的溅蚀力足以使坡面瞬间出露并形成溅蚀坑，从而增强径流紊动性。同时，用于测定流速的染色剂随径流向下流动的过程中有横向的扩散，说明大粒径雨滴的降落时形成的水波也对坡面径流有较大的紊动作用。雷诺数、佛汝德数与雨强的偏相关分析(控制坡长)表明，雷诺数与雨强呈显著正相关，相关系数高达0.896，而佛汝德数与雨强相关性较差，仅为0.013，见表1。

为了进一步分析雨强对坡面径流雷诺数的影响效应，本文建立了回归模型：

表1 雷诺数、佛汝德数与雨强的偏相关性分析

Re=0.286I1.098R2=0.76

式中，Re—雷诺数；I—雨强，mm/h。

回归模型方差分析表明(表2)，F统计量为26.987，显著性概率P值远远小于0.05，且模型决定系数为0.76，说明二者之间确实存在幂函数关系，回归模型的代表性强。

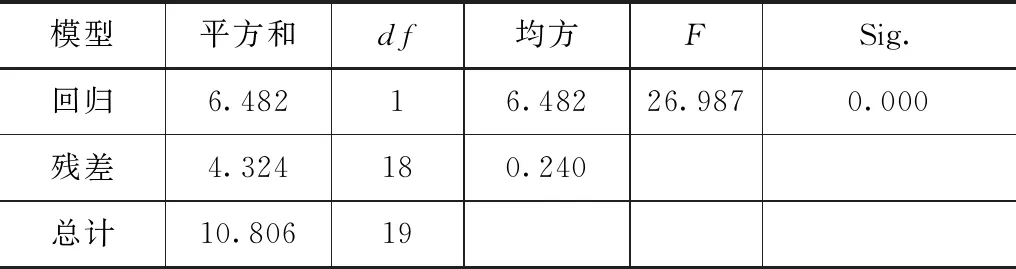
表2 回归模型方差分析

注：自变量为雨强；因变量为雷诺数

2.2 坡长与径流流态的关系

雷诺数、佛汝德数随坡长的变化趋势如图2所示，各雨强下(30～125mm/h)雷诺数随坡长的延长整体呈增大趋势，雨强越大其增速越快增幅越大，而佛汝德数随坡长波动较强，没有规律性。如，雨强30mm/h时，坡长由1m延长到5m，雷诺数分别为7.830、10.359、12.820、12.694、22.371，雨强60、80、125mm/h时，坡长1～5m变化，雷诺数增幅分别为32.14、61.29、65.75，说明径流紊动性随坡长的增大而增强，且雨强越大增幅越大。其原因有两点：一是由于坡面承雨面积与微地貌随坡长延长发生的变化。坡长越长坡面承雨面积越大，径流形成后相同时间内径流量、径流深均较短坡大，且随着坡长延长，由重力势能到动能所转化的能量增大[18]，另一方面，承雨面积越大径流在坡面下部积聚，流速增大，很大程度地增强不同流层之间液体质点的混掺作用。二是坡面微地貌随着坡长的增加变得复杂，则薄层径流局部微小波动增强，从而增加径流紊动性。

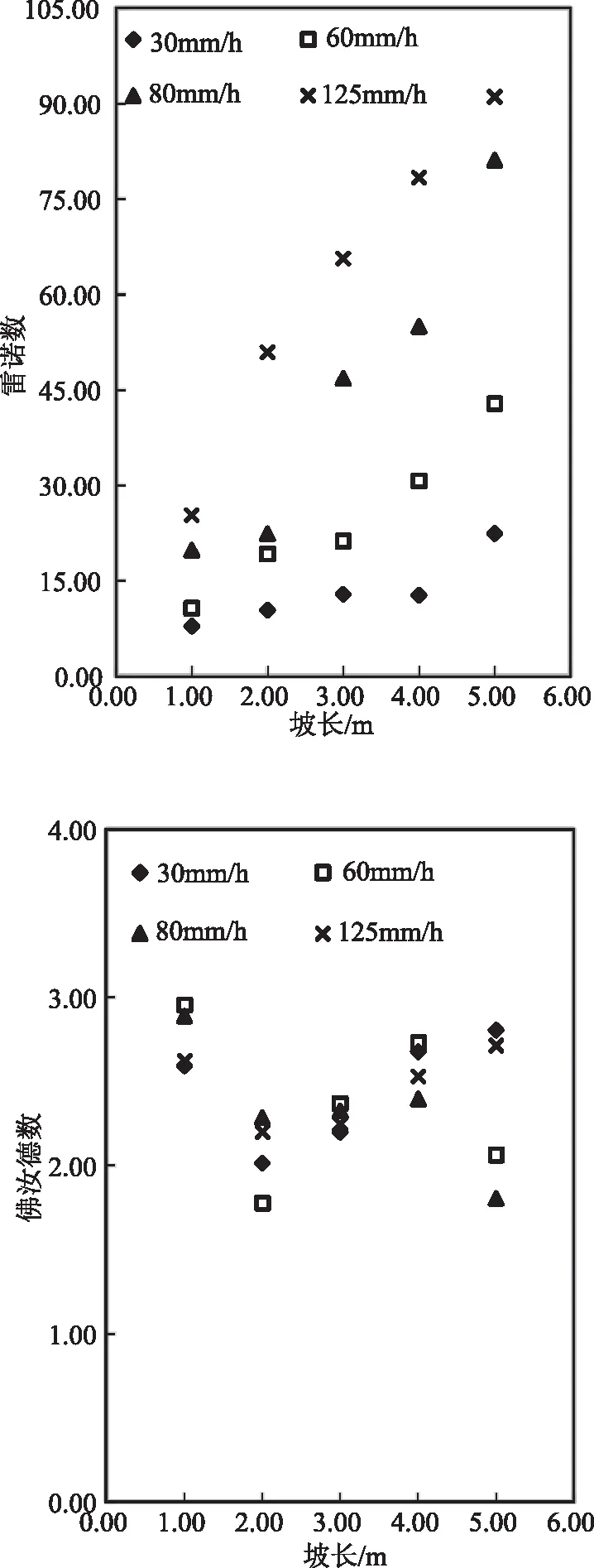
图2 雷诺数、佛汝德数随坡长的变化

雷诺数、佛汝德数与坡长的偏相关分析(控制雨强)见表3，雷诺数与坡长呈显著正相关关系，相关系数高达0.852，佛汝德数与坡长呈微弱负相关关系，相关系数为-0.136。

表3 雷诺数、佛汝德数与坡长的偏相关性分析

为了进一步分析坡长对坡面径流雷诺数的影响效应，本文建立了回归模型：

Re=13.559L0.247R2=0.50

式中，Re—雷诺数；L—坡长，m。

回归模型方差分析见表4，F统计量为9.490，显著性概率P值远远小于0.05，模型决定系数为0.50，说明二者的关系可用幂函数关系较好地表达。

表4 回归模型方差分析

注：自变量为坡长；因变量为雷诺数

2.3 坡长、雨强对径流流态的综合影响

当雨强与坡长同时作用于径流时，二者均与雷诺数具有极显著正相关关系，见表5。雷诺数与雨强的相关系数0.726，而与坡长的相关系数0.586，表明雨强较坡长对径流紊动性影响大。对比表1、3与表5可知，雨强与坡长本身对径流流态均有非常大的影响，其相关系数分别为0.896、0.852，而当二者同时作用于坡面径流时，雨强对径流流态的影响较坡长大，且二者对雷诺数的影响均较单独作用时有所减弱。佛汝德数反映坡面径流流型(急流或缓流)，雨强与坡长无论对佛汝德数单独影响还是二者共同作用时，其相关系数不变，且与雨强呈微弱正相关，与坡长呈微弱负相关，说明二者并非影响坡面径流呈急流或缓流状态的决定因素。

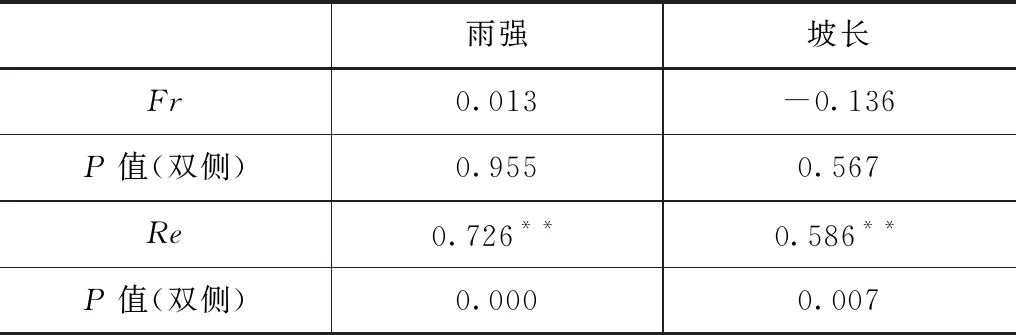
表5 坡长、雨强与雷诺数的相关性分析

注：**表示在0.01水平(双侧)上极显著相关，N=25。

用SPSS对雷诺数与雨强、坡长的关系进行拟合，得出线性回归模型：

Re=0.534I+10.534L-34.697R2=0.87

式中，Re—雷诺数；I—雨强，mm/h；L—坡长，m。

回归模型方差分析表明，模型P值为0.000，远小于0.05，且模型决定系数0.87，说明该模型是显著的且拟合度非常好。回归系数的显著性t检验表明，雨强与坡长的P值均为0.000，远小于0.05，表明雨强与坡长对雷诺数的综合影响可以用线性函数表示。

3 结论

论文基于室内人工模拟降雨手段，分析降雨条件下坡长对晋西黄土裸坡面径流流态的影响，得出以下结论：

(1)雨强30～125mm/h且坡长为1～5m条件下，坡面径流雷诺数均小于500，佛汝德数均大于1，说明坡面薄层径流流态为层流且为急流。

(2)径流雷诺数随坡长、雨强的增大呈增加趋势，且雨强越大其增速越快，坡长越长，雷诺数增加的幅度越大。佛汝德数随坡长、雨强的增大波动较强，没有规律性。雷诺数与雨强、坡长的关系均可用幂函数很好地表达，模型决定系数分别为0.76、0.50。二者对雷诺数的综合影响可用线性方程描述(R2=0.87)。

(3)偏相关分析显示，雨强、坡长与雷诺数均呈正相关关系，相关系数分别为0.896、0.852；当二者同时作用于坡面径流时，雨强对径流流态的影响较坡长大(相关系数为0.726、0.586)，且二者对雷诺数的影响均较单独作用时有所减弱。雨强与坡长无论对佛汝德数单独影响还是二者共同作用时，其相关系数不变，且与雨强呈微弱正相关，与坡长呈微弱负相关，说明二者对于并非影响坡面径流呈急流或缓流状态的决定因素。