基于声波方程转换的三参数递进式全波形反演

何兵红

（中国石油化工股份有限公司石油物探技术研究院，江苏南京211103）

速度是地震成像的关键，在当前单参数全波形反演中占主导地位。为了适应复杂介质，提高地震成像和储层预测精度，降低反演结果解释的多解性，需要利用多种参数提供更加充分信息用以确认地下地层结构和内部充填物质特征[1-2]。对于复杂油气藏，仅利用基于走时信息的射线类反演方法已不能满足当前对精细地震勘探的要求。近十年全波形反演技术发展迅速，同时我国高性能计算集群计算能力不断提高，基于波动方程的多参数全波形反演可以充分利用地震波的运动学和动力学特征对复杂油气藏进行精细刻画，进而为更加准确的储层预测奠定了基础[3-4]。

实际地球介质是复杂的，利用各种复杂介质地球物理模型能够更加逼近真实的地下介质，但基于复杂介质的波动方程地震波数值模拟导致全波形反演计算效率大幅度降低。因此，当前仍然以基于声介质的纵波全波形反演为主[5-6]。

现有的波动方程通常采用纵波速度和密度两个参数对声介质进行描述，因而当提及声波方程多参数全波形反演时，通常是纵波速度、密度双参数反演[7-9]。由于阻抗在储层预测中占据更加重要的地位，综合利用速度、密度、阻抗三参数信息可进一步提高储层预测精度。针对声波方程无法直接反演三参数问题，本文提出了一种基于阻抗-速度方程和速度-密度方程的多参数全波形反演方法：首先利用阻抗-速度方程实现低波数速度模型和阻抗模型的全波形反演，通过方程转换再利用速度-密度方程实现高波数速度反演和密度反演。最后利用SEG 的Overthrust推覆体模型数据进行测试，验证了方法的有效性。

1 方法原理

1.1 三参数反演原理

全波形反演目标函数的非线性源自波动方程的非线性，需要从波场产生机制进行深入理论剖析，进而为多参数全波形反演提供理论指导。对于声介质可以利用纵波速度、密度、阻抗、模量4个参数进行描述。何兵红等[10]研究了6种参数化模式下不同参数的辐射模式，以及每种模式的反演策略。参数之间的耦合性一直是多参数反演的难点问题，反演的参数个数越多，参数之间的耦合性越强，一定程度上降低了反演的精度和可靠性。声波介质中描述储层特征最基本的弹性参数是速度、密度和阻抗，其它参数如拉梅参数、体积模量等都可以通过这3 个参数转换得到。现有的声波方程最多只能用2个参数来表示，三参数同时反演不可行。因此本文需要从双参数全波形反演的特征出发，研究一种可行的基于波动方程转换的反演方法。

图1 3种参数化模式（图中红色表示速度，绿色表示密度，蓝色表示阻抗）a速度-密度模式；b 阻抗-密度模式；c速度-阻抗模式

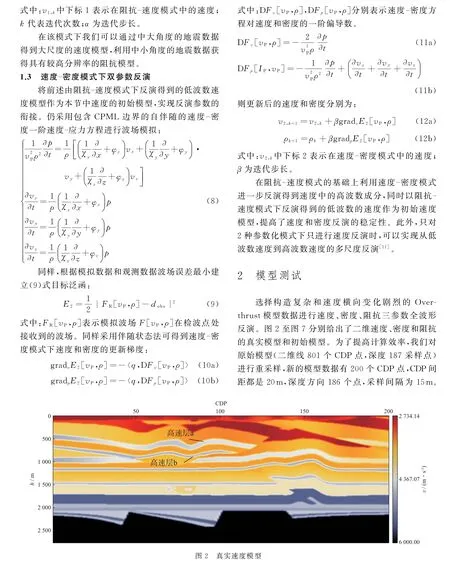
图3 真实密度模型

图4 真实阻抗模型

图5 初始速度模型

模型深度500 m、CDP100左右处存在一个高速层，速度为4540 m/s，其上部地层速度为3300 m/s、下部地层速度3500 m/s，厚度约100 m，我们标记该层为高速层a。在其正下方深度为770 m 处存在另一厚度约为40 m 的更薄的高速层，速度约为4800 m/s，标记该层为高速层b。对于高速层a可分辨的地震数据频率最低为5.7 Hz，对于高速层b可分辨的地震数据频率最低为15 Hz，该分辨频率是在地震波垂直入射的条件下基于可分辨厚度为λ/4（λ为地震波长）得到的。

首先利用主频为10 Hz地震数据进行阻抗-速度以及速度-密度反演，结果见图8和图9。在阻抗-速度模式中速度主要利用大偏移距数据进行低波数的速度更新，阻抗则可以利用小偏移距数据进行阻抗更新，明显看出阻抗模型的分辨率远高于速度模型，两个高速层在速度模型上没有体现出来（图9）。在深度250～500 m，CDP130附近的断层构造在阻抗中得到了较好的刻画（图8）。

图6 初始密度模型

图7 初始阻抗模型

进一步，利用主频为10 Hz的地震数据进行速度-密度反演。在速度-密度模式中由于地震数据中的小角度地震数据参与了速度反演，浅层的断层构造更加清晰，高速层b得到了进一步反演，而高速层a变化并不明显（图10）。但是全波形反演得到的密度反演结果与真实构造特征相差甚远，密度反演不稳定（图11）。同时基于第一步阻抗-速度反演的结果，利用阻抗、速度、密度三者之间的关系经过数学运算得到密度模型（图12），由于采用除法运算，密度更不稳定。

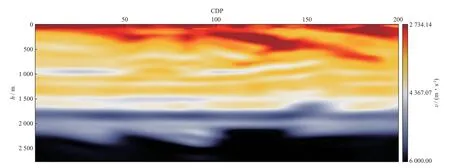
图9 阻抗-速度模式下主频10 Hz全波形反演结果（速度）

图10 速度-密度模式下主频10 Hz全波形反演结果（速度）

图11 速度-密度模式主频10 Hz全波形反演结果（密度）

图12 密度模型（将主频为10 Hz的全波形反演的阻抗与速度相除得到）

图13 阻抗-速度模式下主频为30 Hz的全波形反演结果（阻抗）

图14 阻抗-速度模式下主频为30 Hz的全波形反演结果（速度）

针对主频为10 Hz的地震数据分辨率不足问题，本文利用主频为30 Hz的地震数据开展阻抗-速度以及速度-密度反演，结果见图13和图14。此时在阻抗模型中2个高速层和浅层断层都得到非常清晰的刻画（图13），速度虽然仍以低波数为主，但主要的构造特征得以充分体现（图14）。进一步进行速度-密度反演，结果见图15和图16。此时速度模型中2个高速层更加接近真实模型，构造起伏形态与真实模型完全一致，浅层的断层边界清晰，断面干脆，满足了精细地震勘探对速度的要求（图15）。但是当速度和密度同时反演时，高频时密度的反演更加不稳定，特别是2个高速层的影响导致密度反演结果完全失真（图16）。在速度准确的情况下，通过速度-密度方程可得到较为可靠的密度反演结果（图17）。在该种条件下，本文在利用速度-密度模式进行反演时，采用顺序反演策略，首先得到精度较高的速度模型（图15），并以此作为初始模型进行密度反演。同时在密度反演中通过加入加德纳经验公式对密度值的阈值进行约束，从而得到更加稳健的密度模型（图18）。图19 对比了CDP100 处约束前、后密度反演的结果，可以明显看出，经过约束后的密度反演更加稳定。

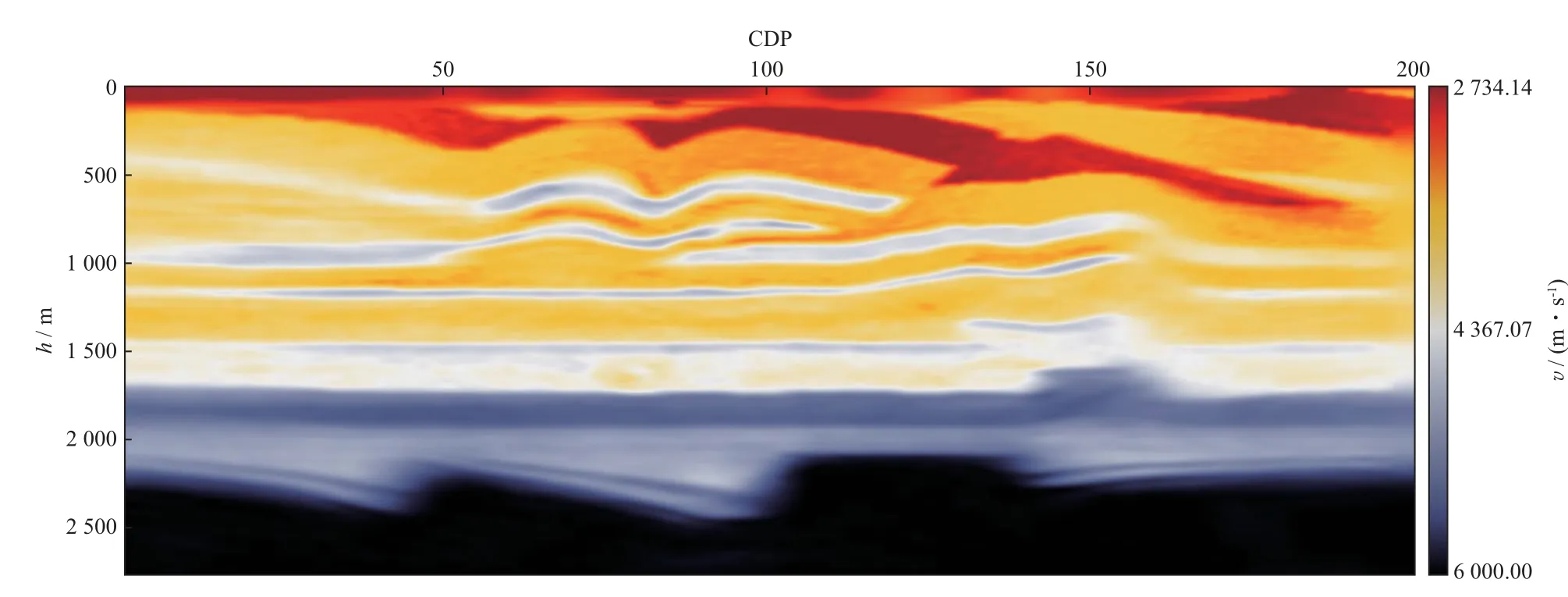
图15 速度-密度模式下主频为30 Hz的全波形反演结果（速度）

图16 速度-密度模式下主频为30 Hz的全波形反演结果（密度）

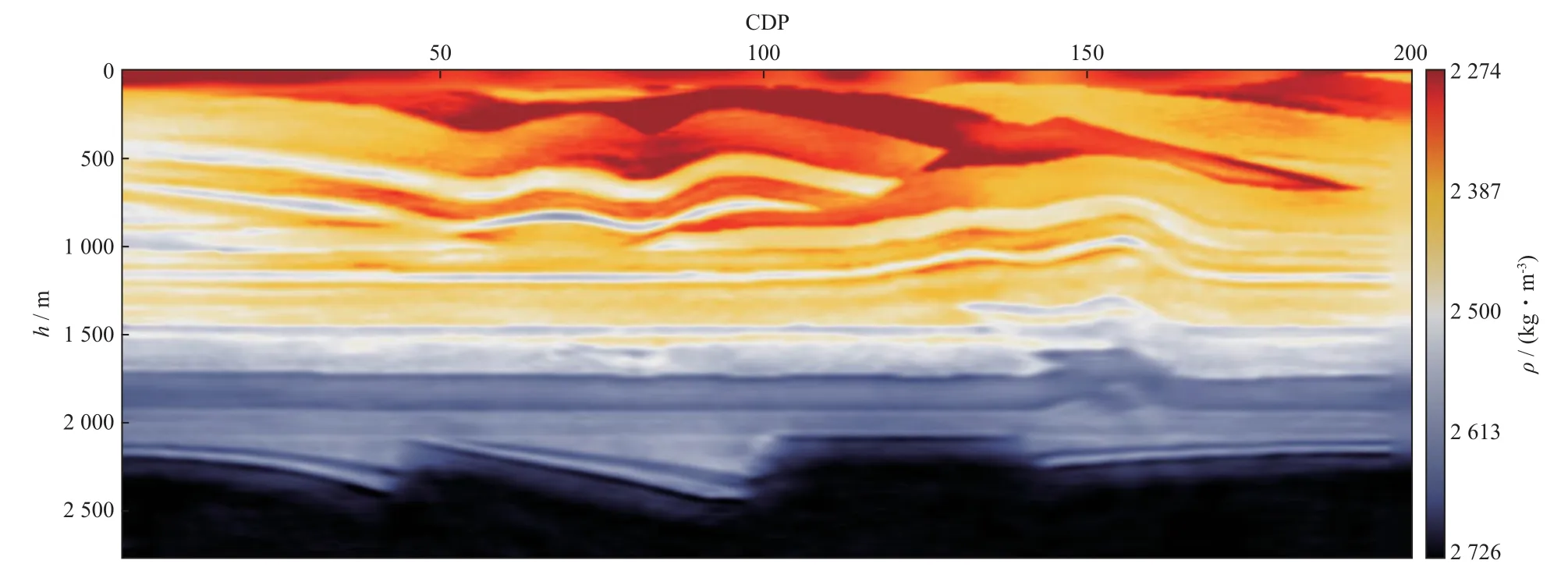
图17 速度准确时主频为30 Hz的密度反演结果

图18 加入加德纳经验公式约束下主频为30 Hz的密度反演结果

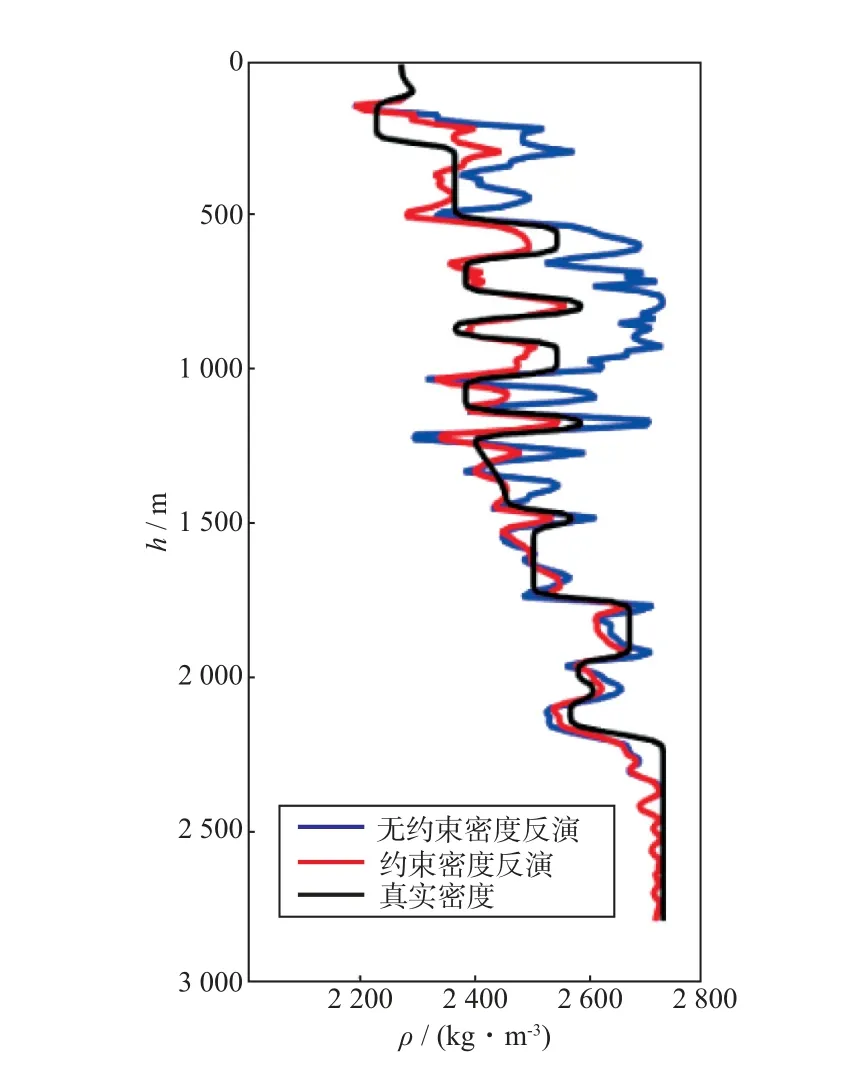
图19 密度反演结果对比

3 结论与认识

本文提出了一种三参数全波形反演方法，首先利用阻抗-速度方程实现低波数速度模型和阻抗模型的全波形反演，然后通过方程转换再利用速度-密度方程实现高波数速度反演和密度反演。该方法以低波数到高波数速度为衔接，将2种双参数全波形反演结合实现声波方程下的三参数全波形反演。将三参数全波形反演分解为2个双参数全波形反演，体现出两方面的优势。

1）常规声波方程大多采用密度固定只用速度表示的单参数方程或双参数方程，方程中参数个数小于需要反演参数个数，常规的三参数同时反演不可实现，本方法通过方程转换的形式实现了基于声波方程的三参数直接反演；

2）将三参数反演分解为双参数反演，弱化了反演过程中多参数之间的耦合性，通过递进式的反演策略提高了反演结果的可靠性。同时将阻抗-速度模式中得到的低波数的速度作为速度-密度模式下的初始速度模型，进一步提高了速度和密度反演的稳定性。

基于复杂的Overthrust 推覆体模型对主频10 Hz和30 Hz地震数据进行反演，得出的速度和阻抗构造起伏形态与真实模型吻合，特别是断层边界刻画非常清晰、断面干脆，满足了精细地震勘探对速度和阻抗的要求。主频越高反演结果分辨率越高，对波动方程的稳定性要求也提高，计算量增大，在实际资料反演中可根据目的层厚度确定合适的主频。此外本文通过加入加德纳经验公式对密度的阈值进行约束提高了密度反演的稳定性，但对于实际数据已知的信息与真实地下情况相差甚远，经验公式约束方法的实用效果会远不如模型数据，这也是今后需要解决的问题之一。