钻遇大型溶洞的油井参数及储层参数动态评价方法

于清艳，胡向阳，李 勇，贾 英

(1.中国石化 石油勘探开发研究院，北京，100083； 2.中国石油 勘探开发研究院，北京，100083)

近年来，随着中国油气勘探开发程度越来越高，开发难度也逐渐增大。总体上，勘探开发由陆相向海相转移，由碎屑岩储层向碳酸盐岩储层转移[1-2]。通过地震反演和储集体静态雕刻可知，碳酸盐岩储层可分为裂缝型、缝洞型、基质孔隙型以及溶洞型等多种类型[3-6]。中国缝洞型碳酸盐岩油藏多以洞穴型为主，且连通性差，油水分布复杂。近年来缝洞型油藏实现了快速上产，但由于油气富集模式多样，且存在渗流、自由流等多种流动状态，导致缝洞型储集体发育模式及其分布规律认识不清，静态雕刻储量不够准确，同时储集体油井参数和储层参数无法通过静态方法准确确定。

针对此类缝洞型复杂储层，在数学表征方面国内外学者已进行了一些研究。常见的数学表征方法为通过引入三重孔隙的概念，建立了三孔单渗模型[7-12]和三孔双渗模型[13]，并在多重介质的基础上进行了试井理论研究[14-16]，此外，部分学者还以管流[17-19]、渗-管流耦合[20-21]等理论为基础进行了相关理论研究。例如，Li等[22]利用试井等动态诊断手段将缝洞型碳酸盐岩储集体分为两大类：均质型和复合型，其中根据储集体内部具体的孔洞缝分布，复合型储集体包括径向复合内好外差、径向复合内差外好等类型，并对不同储集体油井的生产特征进行了评价。杨磊等[23]通过研究缝洞型碳酸盐岩储层，将其储集体类型分为均匀基质、封闭溶洞、双重介质和串珠状储层4类，并为这4类分别选定了试井解释数学模型近似处理：均质模型、径向复合、双重介质、串并联模型[24-25]。总体来说，目前对于尺度较小的裂缝型或溶洞型储层，多用均质多重模型来描述；对于内外区缝洞发育情况不同的储层，多用复合均质多重模型来描述，模型中流体流动大多仅考虑为渗流。可见，不同的缝洞空间组合可以简化为不同的储集体模式，进而决定了油井不同的生产动态曲线形态[26-28]。

本文主要针对钻遇大型溶洞的油井，在目前储集体静态地质雕刻认识的基础上，将大型溶洞与其周围储层简化为单洞与多重介质复合模型，其中，大型溶洞中的流体流动等效为自由流，多重介质中的流体流动等效为达西渗流，建立了相应渗流-自由流耦合数学模型，通过解析求解得到了油井产量不稳定分析曲线，同时经过规整化处理[29-32]，获得了归一化的Blasingame拟合图版，进而经过图版的拟合，形成了油井参数、溶洞参数和其他储层参数等的评价方法和流程，用以指导缝洞型碳酸盐岩油藏的开发。

1 数学模型建立

当碳酸盐岩储层中发育大型溶洞，且溶洞周围分布均匀的小尺度孔洞缝储层时，可用简化大型溶洞与多重介质复合模型进行求解。

1.1 物理模型

图1为单洞与多重介质复合模型，油井直接打在溶洞上，溶洞周围为多重介质储层。其中，储集体简化为三维圆柱复合模型，大型溶洞为内部圆柱体，圆柱高度为h，半径为R；外部为多重介质，与圆柱体同心。模型作如下假设：①油井以定产量q生产；②油藏依靠弹性能开采；③流体弱可压缩，且其压缩系数为常数；④大型溶洞弱可压缩，且其压缩系数为常数，其内流体为自由流；⑤周围储层考虑为渗流；⑥忽略重力、井筒储集效应和表皮效应的影响。

图1 单洞与多重介质复合模型Fig.1 The composite model of reservoirs of cavern-only and multi-porosity mediaa.静态雕刻示意图；b.物理模型示意图

1.2 渗流-自由流耦合数学模型

模型的周围储层以三重介质为例，且周围储层流体通过裂缝流入大型溶洞，同时周围储层基质和溶蚀孔洞向裂缝中窜流。

流体在周围储层裂缝中渗流的偏微分方程为：

(1)

流体在周围储层溶蚀孔洞中渗流的偏微分方程为：

(2)

流体在周围储层基质中渗流的偏微分方程为：

(3)

周围储层通过裂缝与大型溶洞相连，由大型溶洞质量守恒定律可得，

(4)

大型溶洞考虑为自由流的等势体，则大型溶洞中，

pf|r=R=pw=pV|r=R

(5)

封闭外边界条件为：

(6)

初始条件为：

pv|t=0=pf|t=0=pm|t=0=pV|t=0=0

(7)

式中：R为大型溶洞半径，m；r为任一点到井的径向距离，m；；re为泄油半径，m；q为油井的地面产量，m3/d；t为生产时间，h；Bo为原油体积系数，无量纲；μ为原油粘度，mPa·s；Kv，Kf，Km分别为周围溶蚀孔洞系统、裂缝系统、基质系统渗透率，10-3μm2；pm，pv，pf，pw，pV分别为周围基质系统、溶蚀孔洞系统、裂缝系统、井底和大型溶洞压力，MPa；Φm，Φv，Φf，ΦV分别为周围基质系统、溶蚀孔洞系统、裂缝系统和大型溶洞的孔隙度；Ctm，Ctf，Ctv，CtV分别为周围基质系统、裂缝系统、溶蚀孔洞系统和大型溶洞的综合压缩系数，1/MPa；αm，αv分别为周围基质系统、溶蚀孔洞系统形状因子，1/m2；h为储层厚度，m。

引入下列无因次变量：

(8)

(9)

(10)

(11)

(12)

(13)

(14)

式中：rD为无因次半径，无量纲；rw为井筒半径，m；reD为无因次泄气半径，无量纲；RD为无因次大型洞穴半径，无量纲；pf,m,v,VD分别为周围裂缝系统、基质系统、溶蚀孔洞系统和大型溶洞无因次压力，无量纲；pi为原始地层压力，MPa；λm,v分别为周围基质系统、溶蚀孔洞系统向裂缝系统的窜流系数，无量纲；ωf,m,v,V分别为周围裂缝系统、基质系统、溶蚀孔洞系统和大型溶洞储容系数，小数。

则，整体油井无因次流动数学模型为：

(15)

式中：pwD为无因次井底流压，无量纲。

经拉普拉斯变换后：

(16)

联立方程，可得以上方程的通解，

(17)

式中：A，B为常数，无量纲；K0为第二类零阶虚宗量变形贝塞尔函数；I0为第一类零阶虚宗量变形贝塞尔函数。

对公式(17)求导后，代入公式(16)中的内边界和外边界条件，可得无因次井底流压Laplace空间解：

(18)

其中，

(19)

(20)

(21)

(22)

式中：K1为第二类一阶虚宗量变形贝塞尔函数；I1为第一类一阶虚宗量变形贝塞尔函数；Y1，Y2，Y3，σ分别为中间变量。

利用Duhamel原理，井底无因次产量拉氏解为：

(23)

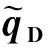
2 常规产量不稳定敏感性分析

对上述拉氏解进行数值反演，以无因次产量qD、无因次产量积分qDi和无因次产量积分导数qDid的对数作纵坐标，以无因次时间tD的对数为横坐标，绘制油井产量不稳定分析曲线，如图2所示。

从图2可以看出，单洞与多重介质复合模型特征曲线可以分为七个阶段：Ⅰ为大型溶洞反应阶段，相当于一个扩大的“井筒”，表现出井筒储集效应，无因次产量积分与产量积分导数曲线重合为斜率为“-1”的直线；Ⅱ 为外围多重介质裂缝线性流与径向流反应阶段，主要与多重介质中裂缝的性质有关；Ⅲ 为外围多重介质中溶蚀孔洞向裂缝窜流阶段，无因次产量积分导数曲线出现第一个“凹子”；Ⅳ 为多重介质裂缝与溶蚀孔洞整体的径向流阶段，无因次产量积分与产量积分导数曲线平行；Ⅴ为多重介质中基质系统向裂缝窜流阶段，无因次产量积分导数曲线出现第二个“凹子”；Ⅵ 为外围多重介质整体径向流阶段；Ⅶ 为边界控制流阶段，对于封闭边界，产量积分曲线与产量积分导数曲线重合为斜率为“-1”的直线。且若ωv=0，单洞与三重介质复合模型可以简化为单洞与双重介质复合模型；若ωv=0，ωf=0.8，模型可以简化为单洞与单重介质复合模型。

图3为单洞与多重介质复合模型油井产量不稳定分析曲线影响因素的敏感性分析。由图3a可以看出，中心大型溶洞半径RD越大，无因次产量积分与产量积分导数曲线相交的直线越靠上，反映的井筒储集效应阶段持续时间越长。图3b中，ωV对曲线的影响与RD类似，但影响相对较小。图3c中可知，随着周围储层泄气半径reD的增大，边界控制流阶段曲线是逐渐靠后的。由Blasingame理论可知[29-32]，运用常规产量不稳定分析图版，由于边界控制阶段曲线的变化，拟合获得的储层参数和油井参数存在多解性问题。

图2 油井产量不稳定分析曲线Fig.2 Oil production variation analysis curves

图3 不同参数对产量不稳定分析曲线的影响Fig.3 Impact of different parameters on the production analysis curvesa. RD对产量不稳定分析曲线的影响；b. ωv对产量不稳定分析曲线的影响；c. reD对产量不稳定分析曲线的影响

3 Blasingame典型曲线图版的绘制

通过Blasingame变换[29-32]，利用公式(24)—(27)，最终可获得无因次规整化产量qDd、无因次规整化产量积分qDdi以及无因次规整化产量积分导数qDdid随物质平衡时间tDd的变化曲线。

(24)

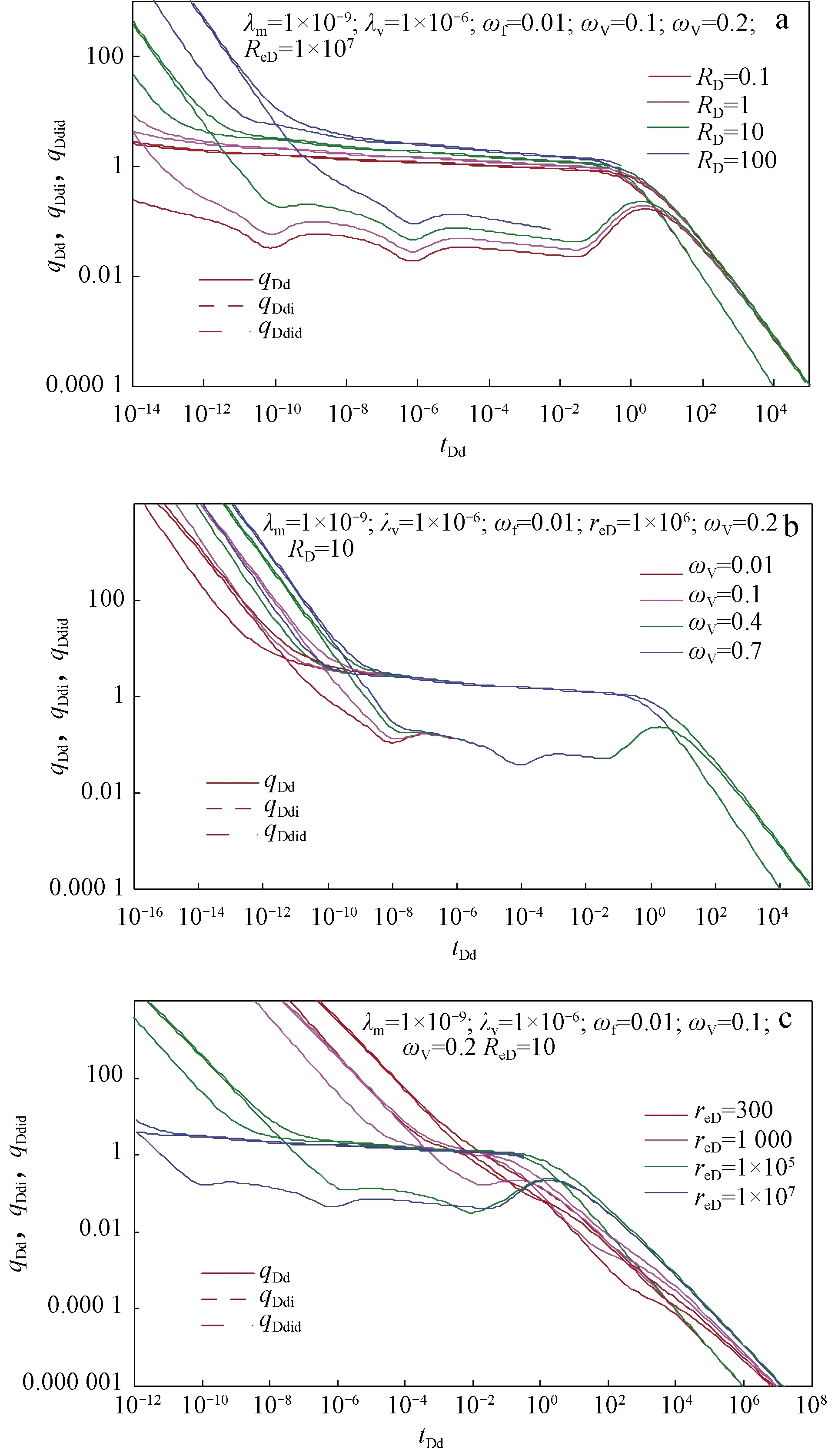
图4 Blasingame典型曲线图版敏感性分析Fig.4 Parameter sensitivity analyses of typical Blasingame curvesa. RD对产量不稳定分析曲线的影响；b. ωv对产量不稳定分析曲线的影响；c. reD对产量不稳定分析曲线的影响

(25)

(26)

qDdid=qDdi-qDd

(27)

式中：qDd为无因次规整化产量，无量纲；qDdi为无因次规整化产量积分，无量纲；qDdid为无因次规整化产量积分导数；tDd为无因次物质平衡时间，无量纲。

经过变换，可得单洞与多重介质复合模型的Blasingame产量不稳定分析典型曲线图版，其参数敏感性分析如图4所示。

由图4c可以看出，Blasingame典型曲线早期的不稳定流阶段为一组对应不同无因次井控半径reD的曲线，reD越大，曲线的不稳定流阶段越往下，而曲线的边界控制流阶段汇聚成一条斜率为“-1”的直线，其值不会随着reD的改变而左右移动。可见，经过Blasingame变换的处理，reD不再影响边界控制流阶段，仅影响不稳定流阶段，这对于储层参数的拟合，尤其对于动态储量的获得减少了较多的不确定性。

4 典型曲线图版拟合步骤

根据常规单重介质封闭储层Blasingame拟合方法可知[29-32]，规整化处理后的实际生产数据拟合典型曲线图版的不稳定流阶段可获得泄油半径、储层渗透率等参数，拟合典型曲线图版的边界控制流阶段可确定油井动态储量等参数。则对于大型溶洞与多重介质复合储层，可根据缝洞体静态储集体模型，选择合适的大型溶洞与多重介质Blasingame拟合图版进行拟合，具体的操作步骤为：

1) 油井实际生产数据的规整化处理，根据公式(28)—(31)可获得油井实际生产数据的规整化产量qDd、规整化产量积分qDdi、规整化产量积分导数qDdid以及物质平衡时间td；

2) 绘制规整化参数与物质平衡时间的三条曲线；

3) 结合储层静态储集体模型，规整化后的实际生产数据通过拟合不稳定流阶段图版曲线，可确定大型溶洞半径、周围储层的泄气半径、周围储层的渗透率等参数；通过拟合边界控制流阶段图版曲线，可确定周围储层的动态储量，且通过与大型溶洞结合，根据公式(32)可确定油井的最终动态储量。

(28)

(29)

(30)

(31)

(32)

式中：td为油井物质平衡时间，d；qd为油井规整化产量，m3/(d·MPa)；qdi为油井规整化产量积分，m3/(d·MPa)；qdid为油井规整化产量积分导数，m3/(d·MPa)；Np为油井累计产油量，m3；q为油井日产油量，m3；pwf为井底流压，MPa；N为油井动态储量，m3；Ct为周围储层综合压缩系数，MPa-1；Sw为大型溶洞水的饱和度，小数。

5 实例应用

塔里木油田某井钻井资料显示，当钻遇目的层位时，出现钻杆放空和泥浆大量漏失等现象，说明井钻遇了大型溶洞或裂缝。由静态储集体模型可知，T1井是通过大型溶洞与周围多重介质储层相连的一口油井，其初期产量相对较高且投产油压高，其生产动态曲线如图5所示。

基于以上大型溶洞与多重介质复合模型Blasingame图版拟合方法及步骤，处理T1井的生产数据并进行图版拟合，拟合结果如图6所示。由拟合结果可知，无因次大型溶洞半径RD为20，泄气半径reD为300，qd/qDd=1/0.08，td/tDd=1/0.02。则计算得到大型溶洞半径约为2.14 m，由公式(32)可计算得到评价的动态储量大小约为27.95×104m3，解释结果与现场实际地质和钻井数据吻合较好。可见，通过图版拟合，利用油井的生产数据即可快速确定大型溶洞参数、周围多重介质参数以及油井动态储量等油井参数，同时可判断油井生产状况，最终指导油藏下一步合理开发部署。

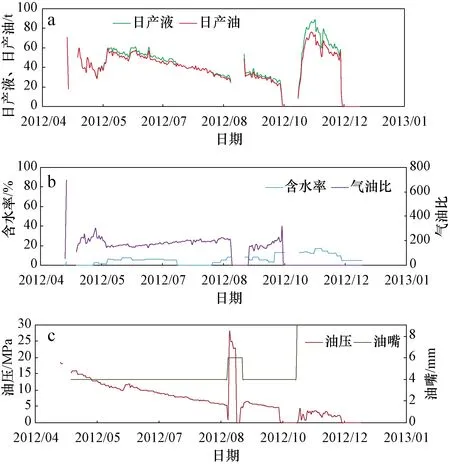
图5 塔里木油田T1井生产动态曲线Fig.5 Curves of the dynamic production data in Well T1,Tarim Basina.日产液和日产油变化曲线；b.含水率和气油比变化曲线；c.油压和油嘴大小变化曲线

图6 油井实际生产数据归一化曲线图版拟合结果Fig.6 Fitting of the cross-plots of normalized Blasingame typical curves with actual production dataa.图版拟合前；b.图版拟合后

6 结论

1) 缝洞型碳酸盐岩储层由于大型溶洞、溶蚀孔洞和裂缝的存在，流体流动包含自由流、渗流等多种流动形式。

2) 针对钻遇大型溶洞的油井，可简化为大型溶洞与周围孔缝储层组成的复合模型，其中大型溶洞中为自由流，井周储层中为多重介质渗流，最终建立了渗流—自由流耦合的数学模型，并进行了求解，获得了油井的产量不稳定分析曲线，并进行了敏感性分析。

3) 通过规整化处理，获得了大型溶洞与多重介质复合模型的Blasingame典型曲线图版，边界控制流阶段曲线归一化，减少了图版拟合过程的不确定性。

4) 通过图版拟合，最终可确定大型溶洞参数、周围多重介质参数以及油井动态储量等油井参数，同时可判断油井生产状况，是否有能量补充和水侵等，为实际油井的合理开发提供技术支撑。