致密砂岩储层多尺度裂缝三维地质建模方法
2020-06-23董少群吕文雅夏东领王世佳杜相仪
董少群,吕文雅,夏东领,王世佳,杜相仪,王 涛,伍 岳,管 聪
[1.油气资源与探测国家重点实验室,北京 102249; 2.中国石油大学(北京) 理学院,北京102249;3.中国石油大学(北京)地球科学学院,北京102249; 4.中国石化 石油勘探开发研究院,北京100083;5.中国石油 青海油田分公司采气二厂,甘肃 敦煌 736202; 6.中国地质科学院,北京 100037]
致密砂岩储层裂缝系统由不同尺度裂缝组成。大尺度裂缝在油藏范围内发育,一般切割复合砂体和泥岩隔层,其在平面上延伸长度大多为百米级至千米级,在纵向上为数十米级,钻遇井多产出高、含水上升快[1],该级别裂缝主要受控于区域应力场[2];中尺度裂缝在平面上延伸长度为数十米级至百米级,在纵向上为米级至十米级,钻井过程中常伴随泥浆漏失,多为好储层段,钻遇井多高产、稳产[1],该级别裂缝主要受控于次级派生应力场或区域应力场[2];小尺度裂缝主要在单砂体内发育,受泥质夹层、钙质夹层、加积体沉积间断面、岩性变化界面限制,在平面上延伸长度为米级至十米级,在纵向上为厘米级至米级,多表现为高角度的节理型裂缝,具有一定的渗透性和储集空间,对应相对较好的储层,钻遇井一般有一定的产能[1],该级别裂缝主要受控于派生应力场[2]。储层中各尺度裂缝共同构成流体流动的主要通道,直接影响致密油气藏的井网部署与注水开发效果[3-4],因此建立有效的多尺度裂缝系统模型对致密油气藏的开发至关重要。
目前致密砂岩储层裂缝建模的常规方法,一般采用确定性建模与随机建模相结合的思路[5]。确定性建模可通过三维地震资料解释确定大尺度裂缝位置及规模,随机建模则可通过离散裂缝网络建模确定中小尺度裂缝,最后将不同尺度裂缝网络进行叠加融合即可生成多尺度裂缝系统[6-7]。应用离散裂缝网络建模方法建立中小尺度裂缝网络时,裂缝发育强度约束体的确定、趋势约束算法、终止条件和多尺度耦合等是近年来研究的热点和难点。
构建裂缝发育强度约束体的常用方式有:①构造应力场数值模拟结合破裂准则生成裂缝强度约束[8-9];②应用地质统计学协变量方法,以裂缝成像测井解释为主变量,以蚂蚁属性体为约束条件,通过井间插值,获得三维裂缝强度约束体[10];③优选裂缝发育主控因素,采用“熵权赋值法”构建三维裂缝发育强度地质模型[11];④利用叠前地震全方位各向异性预测裂缝,生成裂缝强度约束体[12]。
趋势约束算法存在效率低的问题。原始离散裂缝网络建模方法中假设裂缝位置是均匀分布的,这一点与致密砂岩储层中裂缝空间分布特征不符。因为储层中不同位置岩石力学性质及应力状态差异较大,所以储层中裂缝非均质性较强,因此在应用离散裂缝网络建模生成裂缝网络时,多采用裂缝密度体进行约束[13]。生成这种有趋势的裂缝网络,可以通过约束裂缝中心位置完成,该类方法在空间随机生成某个位置作为裂缝中心,通过对比该点处裂缝密度与0~1的随机数关系决定该位置是否有效,若大于随机数,则该生成的裂缝位置有效,反之无效[14-15]。该点处裂缝密度可以直接使用其所在网格的裂缝密度[14],也可以使用临近位置裂缝密度进行插值获得[15]。这类方法的优点是可以生成符合裂缝密度趋势的三维离散裂缝网络,缺点是算法效率低,因其需要对裂缝位置进行有效性验证,大量无效裂缝位置将被剔除,势必导致建模效率下降。
合理确定终止条件可以使所建模型与真实裂缝网络系统更加逼近。常用的终止条件有:①模型中裂缝数量或密度达到一定预设值[15],这种方式简单易行,难点在于研究区裂缝数量或密度的准确求取;②井轨迹钻遇裂缝数量与模型中井轨迹处裂缝数量相近[14],这种方式的优点是直接使用已知单井岩心观察结果或成像测井裂缝解释结果,避免了第一种方式在推算过程中产生的误差,但由于致密储层多发育高角度裂缝,单井钻遇率随机性较强,而岩心或成像测井横向探测范围有限,强随机性常会导致所建立的裂缝模型偏离真实情况。
多尺度裂缝耦合一直是裂缝研究中的难点。多尺度分析方法一般先将复杂系统按尺度分级,分析不同尺度的特征及关联模式,再按不同级别分别进行分析,最后进行融合建立多尺度模型[6]。现有多尺度裂缝建模多采用这种思路,不同尺度裂缝网络分别采用不同方法进行建模,最终叠加形成多尺度裂缝网络模型[16-17]。不同尺度裂缝之间在数量、规模、分布规律等方面具有一定关联性,例如与断层距离越远裂缝密度越低[18],因此可以使用大尺度裂缝控制小尺度裂缝分布的方式恢复多尺度裂缝网络系统。目前,多尺度裂缝耦合方式相对简单,恢复出的裂缝网络常偏离实际,因此如何合理高效地实现多尺度裂缝耦合,已成为致密储层裂缝网络建模中一个亟待解决的关键性难题。
本文以鄂尔多斯盆地西南部H油田为例,在常规裂缝建模方法的基础上,通过确定性建模获取大尺度裂缝网络模型,通过随机建模方法建立中小尺度裂缝网络模型,两者叠合形成最终复杂的裂缝网络系统。研究主要针对多尺度耦合、终止条件求取和趋势约束算法中存在的问题进行探讨,形成致密砂岩储层多尺度裂缝三维地质建模方法。关于多尺度耦合,将根据不同尺度裂缝规模分布函数的相似性,引入分布函数匹配法恢复多尺度裂缝的规模分布函数。在多尺度耦合的基础上,通过大尺度裂缝信息确定裂缝建模终止条件。关于趋势约束算法效率低的问题,将对密度约束的离散裂缝网络建模方法[14-15]进行改进,以提高致密储层裂缝建模效率。
1 研究区地质概况
1.1 地质背景
鄂尔多斯盆地西南部H油田构造上位于天环坳陷南段,目的层为上三叠统延长组长8油层的致密砂岩储层,储层厚度90~110 m。鄂尔多斯盆地延长组地层相对平缓,表现为西倾的单斜构造,倾角小,发育一系列鼻状构造带[19-20]。研究区亦为西倾的单斜,局部有起伏。由于经历多期构造应力作用,目的层中不同尺度裂缝均较为发育。裂缝的主要生成时期为燕山期和喜马拉雅期[21]。燕山期裂缝走向主要为近东西向和近北西向,而喜马拉雅期裂缝的走向主要为近南北向和北东向[22-23]。研究区目的层为典型致密砂岩储层,岩性以灰白色、灰绿色粉细砂岩和黑色泥岩为主,沉积相主要为辫状河三角洲平原及前缘,储层平均孔隙度为10.8%,平均渗透率为0.4×10-3μm2。
1.2 多尺度裂缝
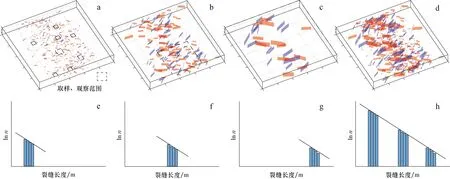
不同尺度裂缝可以通过地表露头、岩心和地球物理等资料获取。不同期次形成的中小尺度裂缝在野外露头均有体现,如陕西省延长县王家河村附近出露的长 8 油层组地表露头[24],可观察到多组高角度构造裂缝,倾角大于60°的裂缝占总数的70%以上(图1a,b)。长 8 油层组岩心上裂缝观察结果表明,该地区目的层主要发育高角度构造裂缝。三维地震资料解释显示,大尺度裂缝的倾角也多为高角度,这一特征与中小尺度裂缝相似。不同尺度裂缝之间存在明显相关性,例如大尺度裂缝附近通常伴生有小尺度裂缝成簇分布(图1c)[25]。
地表露头裂缝描述及已有裂缝研究认识均表明,研究区以构造裂缝为主,中小尺度裂缝走向主要有近东西向、近南北向、北东向和北西向4组[26]。根据裂缝的相互切割关系,近东西向裂缝限制近南北向裂缝(图1a),北西向裂缝限制北东向裂缝(图1b),反映该区裂缝在两期形成,早期形成了东西向和北西向2组裂缝,晚期形成了南北向和北东向2组裂缝[23,27]。值得注意的是,根据三维地震资料解释,该区大尺度裂缝走向与中小尺度裂缝走向并不完全一致,大尺度裂缝的走向主要为近东西向和北西西向[28]。大尺度裂缝与中小尺度裂缝有伴生或派生等多种关系,因此大尺度裂缝的走向与中小尺度裂缝走向略有差异[29]。
根据岩心和地表露头资料显示,小尺度裂缝在垂向上多受岩层面控制,裂缝在岩层内发育并近垂直于层面,岩性界面多为小尺度裂缝的垂向终止界面。中尺度裂缝与层面也近于垂直,但其可以切割岩层面,多受薄层泥岩夹层控制。大尺度裂缝的规模较大,常可以断穿岩性界面和厚度较薄的泥岩夹层。研究区地层较为平缓,中小尺度裂缝与层面近于垂直,并受限于层面等因素,因此,裂缝的形态可近似看成为长宽比较大的高角度多边形。裂缝形态的特征可以指导后续中小尺度裂缝建模中裂缝形状的设计。
2 多尺度裂缝建模原理和方法
2.1 建模原理
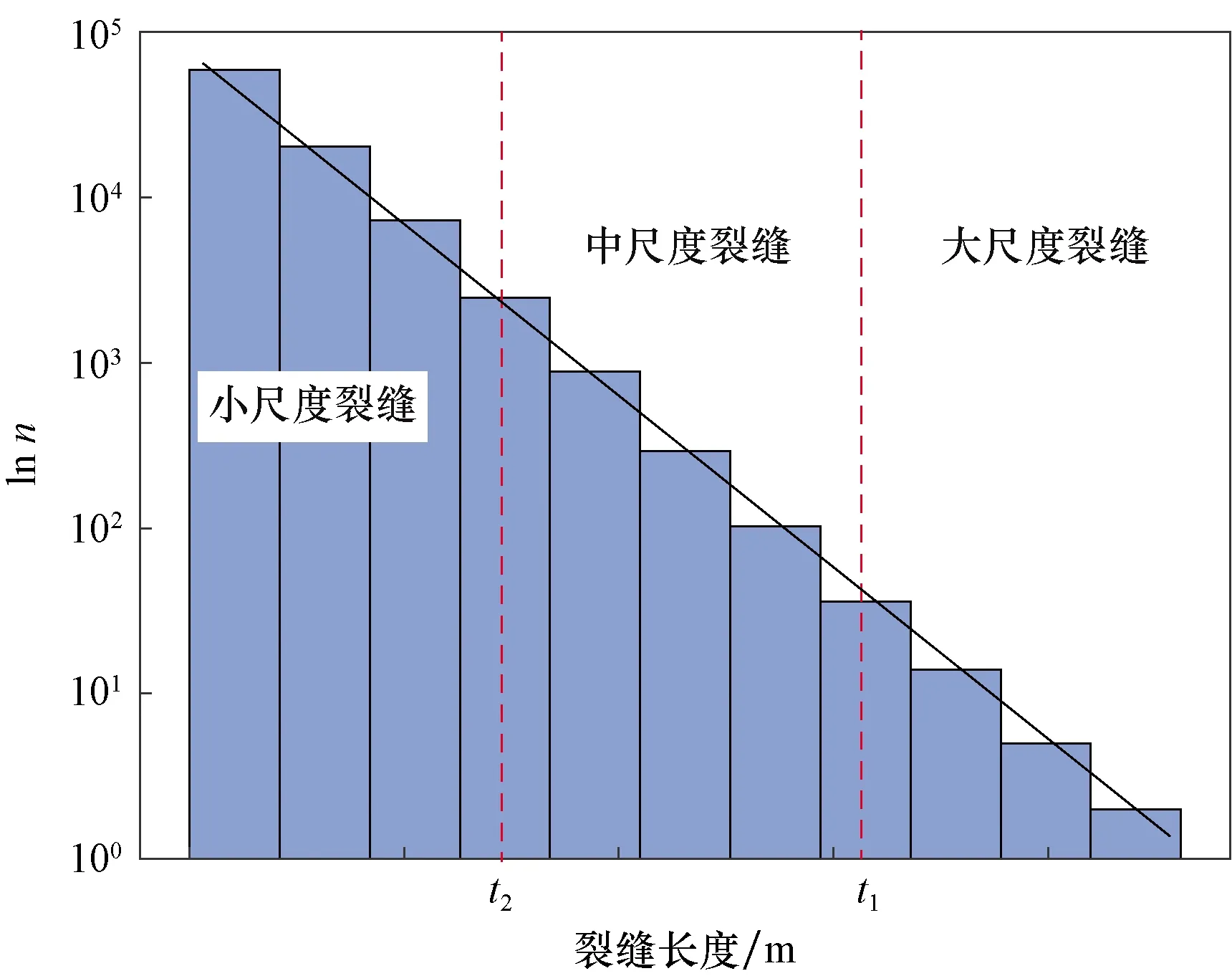
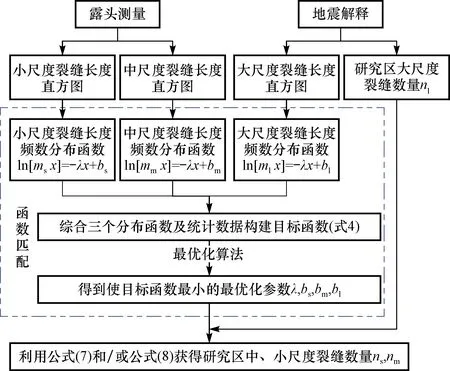
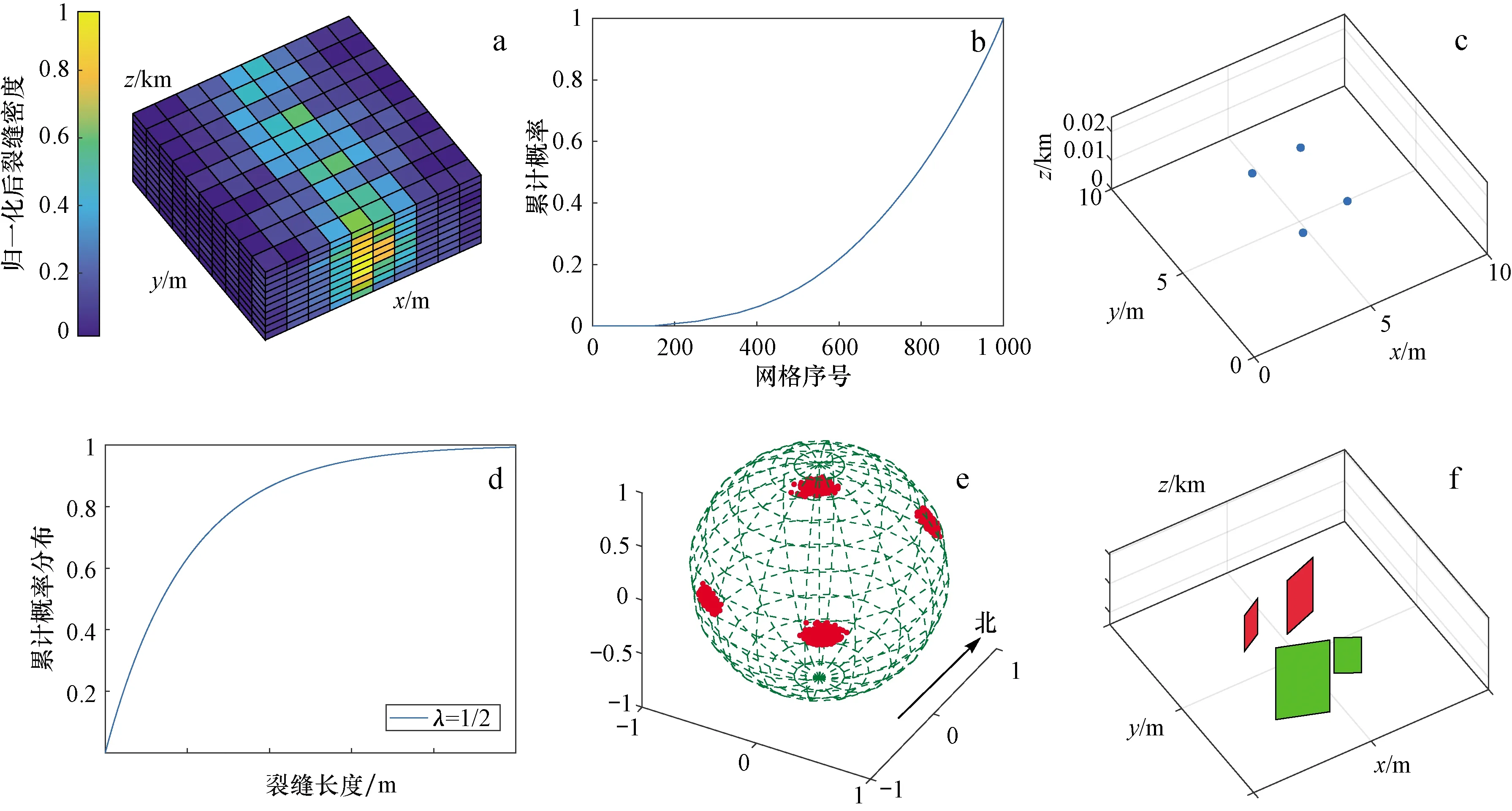
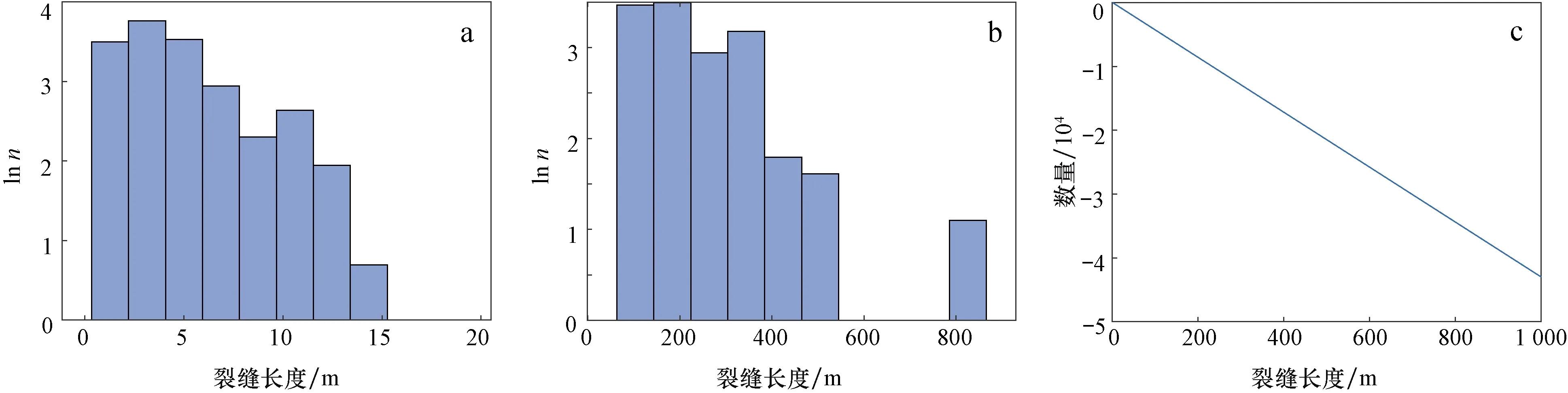
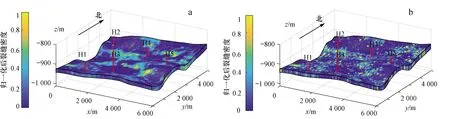
多尺度裂缝系统中裂缝长度多符合指数分布[30-31],其概率密度函数[公式(1)]通过对数变换后可得到变换形式[公式(2)]。利用m(x)替换概率密度分布函数f(x)可得裂缝长度与裂缝数量的关系[公式(3)],m(x)为长度为x的裂缝数量。如图2所示,其斜率为-λ,截距为lnλ+lnn。根据裂缝规模可将其分为大尺度裂缝(x>t1)、中尺度裂缝(t2 图1 鄂尔多斯盆地地表露头区裂缝特征Fig.1 Characteristics of fractures on outcrop in the Ordos Basina.王家河露头区EW向裂缝限制SN向裂缝;b.王家河露头区NW-SE向裂缝限制NE-SW向裂缝;c.大尺度裂缝及其伴生的小尺度裂缝[25] (1) 式中:x为裂缝长度,m;f(x)为裂缝长度的概率密度分布函数;1/λ为分布函数的均值,λ值越大,裂缝平均长度越小。 lnf(x)=-λx+lnλ (2) lnm(x)=-λx+lnλ+lnn (3) 式中:m(x)为长度为x的裂缝数量,条;n为所有裂缝的数量,条。 本文多尺度裂缝建模的思路是,确定性建模获取大尺度裂缝网络,随机建模确定中小尺度裂缝网络。大尺度裂缝常通过地震资料解释获得。中小尺度裂缝建模将选用改进密度约束离散裂缝网络建模方法,具体参见2.3节。所需参数通过裂缝属性(如长度)分布函数匹配获得。根据不同尺度裂缝长度统计结果,可以拟合分布函数,见图2中黑色实线。根据多尺度划分界限t1和t2便可获得大、中、小尺度的裂缝数量(nl,nm,ns),其实现将在2.2节中介绍。 不同类型资料(如岩心、测井、露头、地震等)可以获取不同尺度裂缝的属性信息,例如裂缝大小、走向、倾向、倾角、发育模式等[32-33]。根据不同尺度裂缝属性的关联性进行匹配,可以实现多尺度裂缝信息的耦合,目前,常用于关联性匹配的属性信息便是裂缝规模属性。 图2 裂缝长度分布直方图示意图Fig.2 The schematic histogram of fracture length 本章内容将结合人工生成的多尺度裂缝网络(图3d),对尺度耦合和后续方法原理进行介绍。所用多尺度裂缝网络可以拆解为小、中、大尺度裂缝(图3a—c)。图中黑色虚线矩形框为裂缝信息获取范围。图3a中虚线框对应岩心、小范围地表露头等,具有研究范围小、取样或观测数量多的特点。图3b中虚线框相对较大,对应一定范围地表露头,裂缝信息获取可通过无人机航拍、卫星遥感测量等获得。图3c中虚线框最大,其中的裂缝信息可以通过叠后地震资料断层解释、相干体分析、应力场数值模拟等获得。测量小、中、大尺度裂缝规模信息后,可得到对应的裂缝规模直方图(图3e—g)。由于观测、采样范围不同,各直方图拟合线截距差异较大,但是同时可以观察到各直方图斜率相近,而这一点正是后续多尺度耦合的基础。实际建模过程中,若中小尺度裂缝测量数据较少,则可将中小尺度裂缝进行合并统计,即将图3a,b中结果合并,以减少小样本产生的误差。 不同尺度裂缝规模直方图可以分别恢复出不同尺度裂缝规模分布函数,即可获得函数中的斜率-λ和截距lnλ+lnn[公式(3)]。不同尺度规模分布函数虽有差异,但具有很强的相似性,如图3e—g中所示。根据相似性便可实现多尺度裂缝信息的耦合,具体通过函数匹配,恢复出整个裂缝网络系统的裂缝规模分布函数及裂缝数量。 由于边界效应,直方图两段常出现异常,因此进行函数匹配时将适量剔除两端部分异常数据,仅使用各直方图中间数据。为便于推导,此处假设小尺度裂缝规模直方图中第i个矩形中心的横、纵坐标分别为xi、ms(xi),中尺度裂缝直方图第j个矩形中心的横、纵坐标分别为yj、mm(yj),大尺度裂缝直方图第k个矩形中心的横纵坐标分别为zk、ml(zk)。整个裂缝网络系统的裂缝规模分布函数中关键参数为斜率-λ,可通过寻找使目标函数[公式(4)]最小的参数获得。目标函数Δ(x,y,z)为不同尺度裂缝统计数据与拟合函数的误差平方和总和,最优参数(λ,bs,bm,bl)的求解则通过最优化算法[34]最小化总误差获得,即min Δ(x,y,z)。该优化问题的求解可实现不同尺度裂缝规模函数的匹配。 (4) 图3 通过分布函数匹配对不同尺度裂缝进行耦合Fig.3 Coupling of multi-scaled fractures by distribution function matchinga.小尺度裂缝;b.中尺度裂缝;c.大尺度裂缝;d.多尺度裂缝;e—h对应a—d中裂缝长度分布直方图 式中:x、y、z为小、中、大尺度裂缝规模的向量,x=[x1,x2,…,xn1],y=[y1,y2,…,yn2],z=[z1,z2,…,zn3],n1、n2、n3为小、中、大尺度裂缝规模直方图中矩形的数量;bl、bm、bs为截距。 裂缝规模(常使用平均长度)分布函数的参数λ确定后,便可从大尺度裂缝入手恢复研究区裂缝总数量n。因为相对于中小尺度裂缝,大尺度裂缝是根据整个研究区地震数据或应力场模拟结果获得,其数量基本接近真实分布函数中的数量,因此截距bl=lnλ+lnn可以用于求取所有裂缝数量n=ebl/λ。随后通过指数分布[公式(1)]的累积概率密度函数[公式(5)]即可求得中小尺度裂缝网络中裂缝数量。F(x)=w(x)/n,w(x)为裂缝长度小于x的数量,将其带入累积概率密度函数[公式(5)]便可获得裂缝累积数量w(x)与裂缝长度x的关系[公式(6)]。假设大、中、小尺度裂缝划分的临界值为t1和t2,则利用公式(6)可求得中、小尺度裂缝的数量[公式(7)和公式(8)]。 (5) w(x)=n(1-e-λx) (6) nm=n(e-λt2-e-λt1) (7) ns=n(1-e-λt2) (8) 式中:F(x)为裂缝长度小于x的概率;w(x)为研究区裂缝长度小于x的数量,条;n为研究区所有裂缝的数量,条;nm、ns为中尺度和小尺度裂缝的数量,条;t1为小尺度和中尺度裂缝分界值,t2为中尺度和大尺度裂缝分界值,m。 此处多尺度裂缝耦合可总结为图4中流程图,这一步骤可恢复出的概率密度函数[公式(1)]中参数λ,为2.3节中示性过程提供输入参数,而恢复出的研究区小、中、大尺度裂缝的数量则可为2.3节中裂缝建模提供终止条件。 不同尺度裂缝密度约束体可由多种方式产生,如测井裂缝解释结果三维地质建模、叠前地震各向异性分析、叠后地震属性分析、应力场数值模拟[8,35-36]。裂缝密度约束体获得后,便可通过改进密度约束的离散裂缝网络建模方法分尺度、分组系进行裂缝建模,最终叠加形成多尺度裂缝网络模型。 本节中改进密度约束的离散裂缝网络建模方法,是对文献[14-15]中方法改进。所用建模方法分为两步,即裂缝密度约束的点过程确定裂缝中心位置、示性过程确定裂缝属性(大小、走向、倾向等)。在生成裂缝中心位置时,相比原有建模方法[15],改进方法采用累积概率曲线随机分位数法代替原有的有效性验证,以提高有效裂缝位置生成的效率。方法首先将裂缝密度体(图5a)中所有网格按照裂缝密度值进行排序,随后进行累加以及归一化,生成图5b中累积概率曲线,最后通过生成0~1的随机数作为分位数确定裂缝位置。随机分位数对应累积概率曲线(图5b)的横坐标值即为所选网格序号。在该网格中随机生成位置(x,y,z)作为一条裂缝的中心位置。重复上述过程,直至生成的裂缝数大于预设裂缝条数,即可生成所有裂缝中心,如图5c所示。 图4 不同尺度裂缝进行耦合流程图Fig.4 The workflow showing the coupling of multi-scaled fractures 示性过程将生成每条裂缝的大小、倾向、倾角等属性[37]。露头显示研究区目的层普遍发育高角度裂缝,且受层面控制,因此形状近似矩形。裂缝长度与高度呈正比关系,建模时常采用定比例或者函数关系。因此,只需确定两者中其一即可近似推断出另外一个参数。假设裂缝长度累计概率密度函数已知,见图5d。生成0~1的随机数,作为累计概率密度曲线的分位数,取其横坐标即为裂缝长度,通过比例系数即可确定对应裂缝高度。裂缝倾向、倾角则根据Fisher分布[5,30][公式(9)]依概率生成,如图5e所示。同理可以根据裂缝其他属性累计概率密度分布函数和随机分位数确定裂缝其他属性(如开度)。示性过程中,裂缝属性的累计分布函数约束裂缝网络模型中裂缝特征。每条裂缝的中心位置、大小、产状确定后即可生成离散裂缝网络。 (9) 式中:φ、φ0为描述裂缝倾向的参数,θ及θ0为描述裂缝倾角的参数,φ0、θ0对应优势裂缝的倾向和倾角;κ描述裂缝产状的发散程度,其值越小,发散程度越大[38]。 由于中小尺度裂缝多受层面影响,因此其生成致密储层中小尺度裂缝网络时,应分层、分组系分别执行上述点过程和示性过程,再将其与大尺度裂缝叠加,便可获得最终的多尺度裂缝网络。 中小尺度裂缝长度数据主要通过对出露地表测量获得。由于出露较好的平面地层较少,因此采集的数据量较少。此处,中小尺度裂缝数据共收集164条,因此为了更好的恢复多尺度裂缝的长度分布、减少函数匹配的误差,特将中小尺度裂缝合并统计,所得统计直方图如图6a所示。大尺度裂缝则通过地震资料解释获得,共124条(即nl=124),对应统计直方图如图6b所示。利用2.2节中方法将两者耦合成多尺度裂缝长度分布函数,见图6c,其斜率为-46,根据公式(7)和公式(8)可计算出中尺度裂缝数量nm=6 402、小尺度裂缝数量ns=9 790。 图5 裂缝密度约束的离散裂缝网络建模流程Fig.5 The workflow of discrete fracture network modeling constrained by fracture densitya.裂缝密度模型;b.累积裂缝密度曲线;c.裂缝密度约束下产生裂缝中心;d.确定裂缝大小;e.生成裂缝倾向、倾角;f.生成离散裂缝网络 通过协同序贯高斯模拟,利用单井裂缝解释和裂缝发育强度平面分布,得到中小尺度裂缝密度三维约束体。单井裂缝解释通过岩心、成像测井和常规测井综合。裂缝发育强度平面趋势通过构造应力场数值模拟和叠前地震各向异性分析得到。其中,构造应力场数值模拟建立在地质模型的基础上,考虑了裂缝主控因素(如层厚),因此在实际应用中常更符合地质认识。叠前地震各向异性分析根据裂缝在地震响应上的差异,常能获取分辨率更高的裂缝信息。用于后续中、小尺度裂缝建模的密度约束体如图7所示,从图中可以看出小尺度裂缝密度体展布趋势与中尺度裂缝密度体展布趋势相似,但是更为零星,这也符合较大裂缝附近易于产生裂缝的规律[13,39-44]。 为了确定裂缝形成期次及不同期次裂缝的比例,在露头上进行了大量裂缝走向数据测量,共计984组数据,其所绘制的裂缝走向玫瑰花图见图8a。通过分析各组裂缝数量关系,可以得出各组系裂缝占比约为0.24,0.13,0.3及0.33。随后结合中小尺度裂缝总数nm及ns,即可得出每组裂缝进行随机模拟时的终止条件。 裂缝形成期次及模拟终止条件确定后,将测量所得裂缝走向和倾向数据代入[公式(9)]中Fisher分布,通过最小化分布函数与统计结果的误差,即可获得Fisher分布函数(图8b)中相关参数φ0分别为5°,41°,85°,115°,发散程度参数κ分别为41,24,30,11,倾角相关参数θ0均为83°。 通过1.2节中分析可得,中小尺度裂缝形状为长条状多边形。因而,裂缝网络模型中裂缝将被简化为矩形。不同尺度裂缝建模结果如图9所示。大尺度裂缝空间展布通过地震解释获得(图9a)。中尺度裂缝空间展布通过2.3节中改进离散裂缝网络建模方法生成(图9b)。在叠前地震各向异性分析结果约束下可形成小尺度裂缝模型(图9c)。不同尺度裂缝耦合生成多尺度裂缝系统模型(图9d)。通过对比可以发现,中小尺度裂缝网络中,大尺度裂缝发育位置附近裂缝密度较大,与实际情况相吻合。由于裂缝生成具有层次性,大尺度裂缝对中小尺度裂缝的发育具有明显控制作用[18]。 图6 多尺度裂缝耦合Fig.6 The coupling of multi-scaled fracturesa.中小尺度裂缝;b.大尺度裂缝;c.a和b耦合所得多尺度裂缝 图7 鄂尔多斯盆地H油田裂缝属性分布及中小尺度裂缝密度约束体Fig.7 The distribution of fracture properties and fracture density models of medium and small scales in H oilfield of Ordos Basina.基于构造应力场数值模拟的裂缝数据体;b.基于叠前地震各向异性分析的裂缝数据体 图8 鄂尔多斯盆地H油田裂缝组系、走向、倾向及倾角Fig.8 The group,strike,dip and dip angle of multi-scaled fractures in H oilfield of Ordos Basina.裂缝走向;b.Fisher分布 图9 鄂尔多斯盆地H油田多尺度裂缝耦合Fig.9 The coupling of multi-scaled fractures in H oilfield of Ordos Basina.大尺度裂缝;b.中尺度裂缝网络;c.小尺度裂缝网络;d.多尺度裂缝系统 统计各井在所建立三维裂缝网络中钻遇的裂缝位置及总数,分别与裂缝单井解释、裂缝空间分布、裂缝发育模式、钻井资料、生产资料等进行对比,从而检验所建立模型的有效性。选取研究区具有裂缝单井解释的6口取心井(其中2口为后验井),对比裂缝发育段与模型中对应发育位置,发现岩心上裂缝发育段及测井裂缝异常段在三维裂缝网络模型中均有体现,吻合度较高,而且单井上明显不发育裂缝的层段对应到三维裂缝网络模型中基本无裂缝或少裂缝,说明所建立模型与单井裂缝解释结果具有较好的一致性。 从最终所建立的三维多尺度裂缝网络模型(图 9c)可以看出,裂缝空间分布与裂缝密度约束体(图 7)数值分布规律相近。同时可观察到模型中小尺度裂缝集中发育于大尺度裂缝附近。统计结果表明随距断层距离的增加,所建立模型中裂缝密度近似呈指数下降,这一点与野外露头观察统计所得模式相符。 致密储层中裂缝密度高,储层连通性好,裂缝发育区钻遇井常伴随泥浆漏失、含水上升快等现象[1]。对比不同井目的层段裂缝密度与泥浆漏失情况发现,泥浆漏失严重的井裂缝密度一般较高。对比单井产液量数据与单井裂缝密度发现,含水上升快的井多为裂缝密度高的井。综上可得,所建立的三维多尺度裂缝网络模型与现有资料和已知模式相吻合。 常规裂缝建模多采用确定性建模与随机建模相结合的思路,本文在此框架基础上提出一套针对多尺度裂缝建模的方法。方法对随机建模中关键参数确定和趋势约束离散裂缝网络建模中存在的问题分别提出解决方法,即分布函数匹配法和改进密度约束离散裂缝网络建模方法。 分布函数匹配法可以实现不同尺度裂缝信息耦合,恢复描述多尺度裂缝规模的分布函数,确定不同尺度裂缝网络建模的终止条件和所需分布函数,从而使得分尺度建立的模型更接近真实裂缝网络。值得注意的是,该方法中仍存在一些问题需要解决。如:①分布函数校正的问题,由于不同尺度统计范围的边界会截断部分裂缝,导致统计结果与真实分布函数有所差异,因此需要通过校正才能获得相对准确的分布;②不同尺度裂缝临界值确定的问题,本次研究借鉴了前人发表成果中的临界值,并未对此做深入研究,但临界值对本文所提方法所建立模型有一定影响,将来工作将会对该问题进行进一步研究,如不同临界值对比分析、临界区间代替临界等;③大尺度裂缝平面几何形态多为曲线,而离散裂缝网络模型中裂缝多简化为矩形,因此大尺度裂缝信息统计中的这一问题也将在未来工作中尝试解决。 改进密度约束的离散裂缝网络建模方法用累积概率密度曲线随机分位数法代替原有的有效性验证。在图 7a中,中尺度裂缝密度体约束下生成10 000个裂缝中心位置,使用原始方法[15]和改进方法所需时间分别为658.9 s和23.3 s,所用软件为Matlab2018b,电脑配置为英特尔4710mq处理器,主频2.5 GHz,16 GB内存。在图 7b中,小尺度裂缝密度体约束下做对比试验,也可得出相似结果,原始方法和改进方法所需时间分别为741.3 s和21.4 s。结果表明改进方法在效率方面较原始方法有较大提升,因为原始方法中应用了插值算法和有效性检验,而这两个步骤较为耗时,本文所用的累积概率曲线随机分位数法则通过统计规律实现趋势约束点过程,无需重复。 值得注意的是,野外露头显示中小尺度裂缝多垂直于层面(如砂岩之间的泥岩薄层),且终止于不同层面,因此本文对多尺度裂缝系统进行建模时采用分层的思路。但实际露头中层面间距较小,远小于单砂体级别,为更接近真实中小尺度裂缝网络,需要在进一步精细化层面上做工作[45],并在精细层面的基础上实现层控中小尺度裂缝建模。致密储层的中小尺度裂缝多垂直于层面,而研究区地层相对平缓,且测量所得裂缝多为近似垂直的高角度裂缝,因此本文并未对裂缝模型中倾角校正做过多讨论,但层面变化带来的误差也是影响裂缝建模效果的一个重要因素。后续将在这方面开展工作,以期提高裂缝建模精度。 常规裂缝建模方法通过确定性建模获取大尺度裂缝网络,通过密度约束的随机建模方法确定中小尺度裂缝网络。本文针对该类方法在致密储层多尺度裂缝建模中存在的问题,提出解决方案,汇总形成了一套致密砂岩储层多尺度裂缝的三维地质建模方法。方法可分为4步:①确定性建模获取大尺度裂缝空间展布,如通过地震解释获得;②通过分布函数匹配法对不同尺度裂缝信息进行耦合,以确定建模所需裂缝大小分布函数,并利用大尺度裂缝标定获得建模所需不同尺度裂缝的终止条件;③在不同尺度裂缝密度体的约束下,分层、分组系通过改进密度约束的DFN算法生成中小尺度裂缝网络;④叠加不同尺度裂缝网络形成最终多尺度裂缝网络系统。实例分析中,鄂尔多斯盆地H油田延长组长8地层的应用效果表明该方法建立的三维多尺度裂缝模型与实际资料吻合。
2.2 多尺度裂缝耦合
2.3 裂缝密度约束的离散裂缝网络建模
3 多尺度裂缝三维地质模型建立及检验
3.1 大尺度裂缝与中小尺度裂缝信息耦合
3.2 多尺度裂缝三维地质模型


3.3 多尺度裂缝三维地质模型检验
4 讨论
5 结论
