基于PLSR-BP 复合模型的红壤有机质含量反演研究*

国佳欣，赵小敏†，郭 熙，徐 喆，朱 青，江叶枫

（1. 江西农业大学国土资源与环境学院，南昌 330045；2. 江西省鄱阳湖流域农业资源与生态重点实验室，南昌 330045）

土壤有机质是指土壤中以任何形式存在的含碳有机化合物，它是土壤的重要组成部分。传统的测量土壤有机质的方法主要是化学分析方法，尽管测定结果可靠，但存在着费时费力的问题，难以满足快速监测土壤有机质含量的需求[1]。近些年，土壤高光谱技术的出现为土壤有机质含量的快速预测提供了手段，以其极高的光谱分辨率来获取反映土壤特性的信息，可节省大量的人力物力，也为精准农业提供了重要的监测手段[2-4]。

光谱预处理在可见光/近红外光谱分析中具有重要的作用，传统的土壤高光谱的研究主要是采用原始光谱反射率及其1 和2 阶导数、倒数和对数等方式对光谱数据进行数学变换来构建土壤有机质预测模型。然而仅采用传统的1、2 阶导数来对土壤光谱数据处理时，两者相差过大，会导致中间过渡信息的遗漏[5]。徐继刚等[5]研究汽油近红外光谱时得出分数阶导数的最优结果并不都在整数阶导数处，而是在0 和1 阶导数之间或1 和2 阶导数之间。随着导数阶数的增加会提高光谱分辨率，同时降低光谱信号的强度[6]。Tong 等[6]采用分数阶Savitzky-Golay导数法（fractional order Savitzky-Golay derivation，FOSGD）对近红外光谱模型进行优化，从而提供更好的方法来平衡分辨率和信号强度之间的矛盾。王敬哲等[7]在对荒漠土壤有机碳进行预测时，得出经过分数阶导数预处理后的模型精度较整数阶导数有较大提升，其研究结果表明采用分数阶导数对土壤光谱数据进行潜在信息挖掘是可取的。以上研究充分说明了对于土壤光谱数据进行导数变换时，不应拘泥于传统的整数阶导数，也要考虑分数阶导数变换在数据预处理上的作用。

国内外众多研究表明，运用可见光-近红外波段进行线性的偏最小二乘回归（partial least-squares regression，PLSR）和非线性的 BP 神经网络等单一模型建模的研究较多[8-9]。洪永胜等[10]和Conforti等[11]通过偏最小二乘回归单一方法构建了土壤有机质含量的预测模型。丁国香[12]通过 BP 神经网络方法研究了土壤中的有机质与可见光/近红外光谱之间的关系，并建立相应的预测模型。然而线性模型仅适用于变量较少且具有很大线性关系的情况，非线性模型在输入变量过多时容易出现“过拟合”现象，因此可以考虑线性模型与非线性模型相结合是否能够提高有机质含量的预测精度。

本文以奉新县北部为研究区，基于 PLSR、BP神经网络和PLSR-BP 复合模型，在对红壤光谱数据进行0～2 阶分数阶导数、倒数的对数和对数的导数等数学变换的基础上，对红壤有机质含量预测模型的建立进行探索，以明确最优数学变换和模型的选取，以期为南方红壤地区土壤有机质含量的快速预测提供参考依据。

1 材料与方法

1.1 研究区概况

研究区位于江西省西北部的奉新县北部，115°08′～115°40′E，28°68′～28°80′N，总面积为 2.0×104hm2。研究区属中亚热带湿润气候，年平均气温为17.3℃，年均降雨量为1 612 mm，年均相对湿度为79%。如图1 所示，本文所选研究区域主要包括奉新县赤岸镇、会埠镇、冯川镇、干洲镇和罗市镇的部分村，是以昌德高速（S40）和两条省道（S308和S226）围成的闭合区域。从DEM 图中能够得出，研究区海拔介于31 m 至133 m 之间，处于平原地带。低海拔区域主要分布在东南部地区，而较高海拔区域则分布在研究区北部和西部地区。经实地调查及土地利用现状图统计得出，研究区内主要包括林地1.1×104hm2，水田 5.0×103hm2，园地 1.0×103hm2，其他用地 3.0×103hm2，分别占研究区总面积的55%、25%、5%和15%。

图1 研究区位置、DEM 与采样点分布Fig. 1 Location of the study area and the distribution of DEM and sampling points

1.2 土壤样本采集

样本的采集时间为2018 年7 月23 日至8 月11日，采用1 km×1 km 规则格网划分研究区，在各格网内随机选取采样点，综合考虑地势、植被覆盖、土地利用类型及道路可达性，对于个别地理环境较为复杂的区域，进行了采样点的加密，以保证数据的代表性。在采样点附近5 m 范围内不同方向选取四个重复样点，混合均匀后，用四分法得到最终样本，剔除其中的植物根系和石块等，同时使用手持GPS 仪器读取采样点的位置信息。采集样本覆盖园地、林地、水田三种土地利用类型，其中园地57 个、林地93 个、水田98 个，园地、林地的采样深度为30 cm，水田为20 cm。样本于实验室风干、研磨，过2 mm 筛，并将其均分为两部分，分别用于土壤光谱和有机质的测定。土壤有机质含量采用重铬酸钾容量法测定[13]。

1.3 光谱测量

采用美国 ASD FieldSpec4 地物光谱仪进行土壤光谱反射率的测量。光谱采集范围为 350～2 500 nm，光谱采样间隔为1.4 nm（350～1 000 nm）和2 nm（1 001～2 500 nm），重采样间隔为1 nm，共输出2 151 个波段。在暗室内进行光谱的采集，以避免外界干扰。将土样置于直径6 cm 深2 cm 的黑色盛样皿中，盛满并用直尺将表面刮平。使用MugLite 仪器中自带的内置光源进行测量，将盛样皿置于仪器顶部槽中，每次采集数据之前对仪器进行暗电流和标准白板校正，每个样本采集5 条光谱数据，取其算术平均值作为该样本的光谱曲线。

1.4 光谱预处理

由于环境和仪器自身的影响会对测量光谱的边缘波段造成较大的噪声，因此去除350 nm～399 nm及 2 451 nm～2 500 nm 波段。通过 Daubechies6（DB6）小波进行三层分解，采用软阈值法对高频系数进行去噪处理，去除测量过程中产生的噪声影响[14-15]。研究采用10 nm 间隔进行重采样，得到由205 个波段组成的光谱曲线，以降低数据维数，减小数据冗余。

除上述预处理外，本文还对光谱数据进行下述数学变换，包括光谱反射率（reflectance，R），分数阶导数：0.5 阶导数（fractional order derivative，FOD（0.5））、1 阶导数（FOD（1））、1.5 阶导数（FOD（1.5））、2 阶导数（FOD（2）），倒数的对数（inverse-log reflectance，ILR）和对数的导数（log-derivative reflectance，LDR）。已有研究表明这些变换在土壤光谱研究中有广泛的应用，有助于突出光谱特征，为有机质反演提供更高的模型精度[8，16-17]。其中分数阶导数变换通过MatlabR2017b 编程实现。

分数阶导数（FOD）目前广泛应用于建模、信号分析等领域[18-19]，有三种主要类型的算法，分别是 Riemann-Liouville（R-L），Grünwald-Letnikov（G-L）和Caputo[20]，其中G-L 分数阶导数是由整数阶导数的定义推广而来。分数阶导数有助于光谱信息的增强，在一定程度上减小了噪声对数据的干扰。本文采用G-L 算法求出分数阶导数：

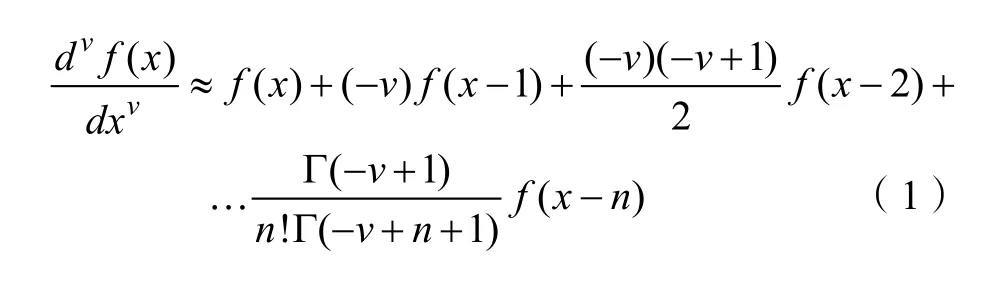
式中，v为阶数，Γ（x）为Gamma 函数，n为导数上下限之差[21-23]。

1.5 模型的建立与评价参数

本文分别采用线性模型PLSR 和非线性模型BP神经网络进行红壤光谱有机质含量估测，再将PLSR与 BP 神经网络模型进行复合，用于有机质含量预测模型的构建。

PLSR 是目前较为常用的一种线性多元回归分析方法，它能够分析预测矩阵 X（即自变量）与响应矩阵 Y（即因变量）之间的关系，将初始输入的数据投影到一个潜在的空间中，利用正交结构提取出大量潜变量，找出这些新变量与 Y 之间的线性关系[24]。采用留一法（Leave-one-out）交叉验证来确定提取出的潜变量个数，建立PLSR模型[8]。

BP 神经网络是人工神经网络中一种应用较为广泛的非线性建模方法，适用于数据预测[9]，其网络结构由输入层、输出层和隐含层构成。学习过程由前向传播和反向传播两方面组成，在前向传播过程中，输入数据由输入层经由隐含层向输出层逐步处理，如果输出层得到的数据误差不在允许范围内，则进行误差反向传播，通过梯度下降法逐层调整各神经元的权重，直至误差符合指定要求[25]。

在利用BP 神经网络进行建模时，减少输入变量的数量可以减小数据之间的相关性。因此采用PLSR 与BP 神经网络相结合的方法，将PLSR 提取出的潜变量作为BP 神经网络的输入层数据，这些新变量能反映原变量的绝大部分信息以达到减少数据量降低维度的目的，从而避免“过拟合”现象的发生[25]。

采用决定系数（R2）、均方根误差（RMSE）、预测偏差比（RPD）作为精度评价指标。R2和RPD越大说明模型越好，RMSE 越小说明预测效果好[26]。当RPD＜1.5 时，表明模型无法对样本进行预测；当1.5＜RPD＜2 时，表明模型只能对样本进行粗略预测；当2＜RPD＜2.5 时，表明模型有较好的预测样本的能力；当RPD＞2.5 时，表明模型有很好的预测样本的能力。式（2）中n为数量，ym和yp分别为有机质实测值与预测值。式（3）中STDEV 计算的是验证集样本实测值的标准偏差。

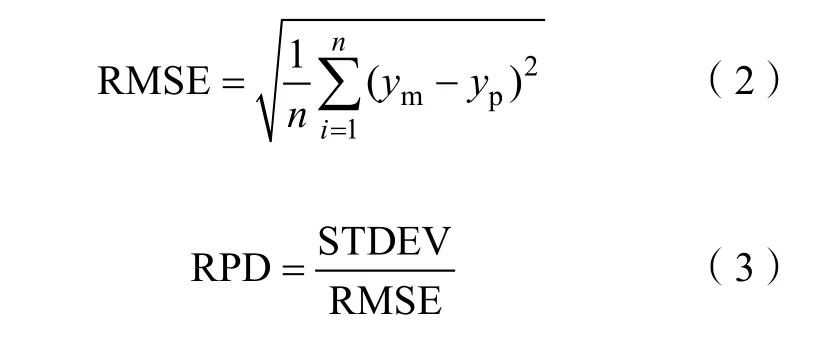
常规数据统计分析软件使用软件ArcGIS 10.5、IBM SPSS Statistics 22.0 、 OriginPro 2016 和Microsoft Excel 2010，PLSR 使用 The Unscrambler X 10.4，BP 神经网络使用Matlab R2017b。

2 结 果

2.1 红壤有机质描述性统计特征

获取的 248 个样本，其有机质含量范围为5.27～64.00 g·kg-1。由于异常值的存在会影响建模精度，因此采用拉依达准则[27]对样本进行检验，发现数据无异常值。将 248 个土壤样本选用 K-S（Kennard-Stone）算法[28]按照样本间的欧氏距离以3︰1 的比例分为两组，其中训练集包含186 个样本，验证集包含62 个样本，用于模型的精度检验。全集、训练集和验证集的有机质含量均值分别为 33.97、35.04 和 30.78 g·kg-1，变异系数分别为 43.27%、41.07%和49.64%，属于中等强度变异（图2）。

图2 红壤样本有机质含量描述性统计Fig. 2 Descriptive statistics of soil organic matter contents in red soil samples

2.2 红壤光谱特征

图3 为经预处理后的红壤光谱曲线，在可见光部分呈陡坎型[15]。从中可以发现在900 nm 左右有较明显的氧化铁吸收谷，因此在建模时去除 800～1 000 nm 波段以减小氧化铁对光谱的影响。而在1 400 nm、1 900 nm、2 200 nm 处有明显的水分吸收谷[29]，考虑到样品已经经过了风干处理，对于有机质含量建模影响较小，不作处理。

研究将有机质含量按高低划分为＜15、15～25、25～35、35～45、45～55、≥55 g·kg-1六组，每个组别内求取其光谱曲线的平均值。从图3 中可以看出，随着有机质含量的增加，在可见光波段内，不同含量的样本光谱曲线相差不大，而在近红外波段，可以看出有机质对光谱的影响较为明显，有机质含量与光谱反射率呈现负相关的现象。500～800 nm部分数据存在交叉现象，可能是由于在可见光部分土壤反射率数值相接近，平均之后相差不大。

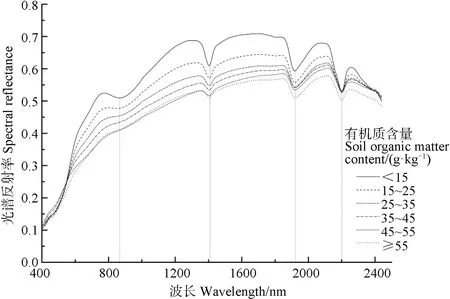
图3 不同有机质含量红壤光谱曲线Fig. 3 Spectral curves of the red soil samples relative to content of organic matter

2.3 红壤有机质含量PLSR 建模

运用经过数学变换后的光谱数据（400 ～800 nm、1 000～2 450 nm）中经过P=0.01 显著性检验后的波段分别建模的自变量，土壤有机质含量作为因变量。从表1 可以看出，PLSR 建模时，R、FOD（2）、ILR 和LDR 模型的RPD 均未达到2.0，模型效果一般，只能对样品有机质含量进行粗略估测；而FOD（0.5）、FOD（1）及FOD（1.5）模型的RPD 分别为2.19、2.23 和 2.34，均在 2.0 以上，说明模型对有机质含量有较好的预测能力。对R进行数学变换后，仅有LDR 的验证集精度下降，R2虽然升高了0.04，但是RMSE 升高了 0.49 g·kg-1，RPD 下降了 0.09。表中数据充分说明数学变换有效地提高了红壤有机质含量的预测能力，其中FOD（1.5）模型的训练集和验证集的R2最高，分别达到了0.88 和0.83，RMSE 分别为 4.98 g·kg-1和 6.62 g·kg-1，预测能力最为显著，其RPD 达到了2.31。

2.4 红壤有机质含量BP 神经网络建模

BP 神经网络模型是将训练集各波段光谱数据作为输入层数据，土壤有机质含量作为输出层数据进行构建。从表2 中可以看出，基于光谱反射率数据（R）的BP 神经网络模型的训练集和验证集精度均不高且RPD 仅为0.89，无法对样本有机质进行预测。FOD（0.5）、FOD（1）、FOD（1.5）、FOD（2）、ILR 和 LDR 模型的训练集R2均达到了 0.90 以上，RMSE 均小于 5.00 g·kg-1；验证集R2基本达到 0.80，RMSE 基本在 7.00 g·kg-1以下，RPD 均在 2.10 以上，具有较好的预测有机质含量的能力。其中ILR 模型训练集R2最高达到了 0.95，RMSE 为 3.14 g·kg-1，但验证集中 FOD（1）模型R2最高为 0.84，RMSE为 6.55 g·kg-1，RPD 为 2.34。结合表 1 和表 2 可以看出，与 PLSR 相比，BP 神经网络 R 模型的 RPD下降了0.86，其余变换RPD 均有所提升。

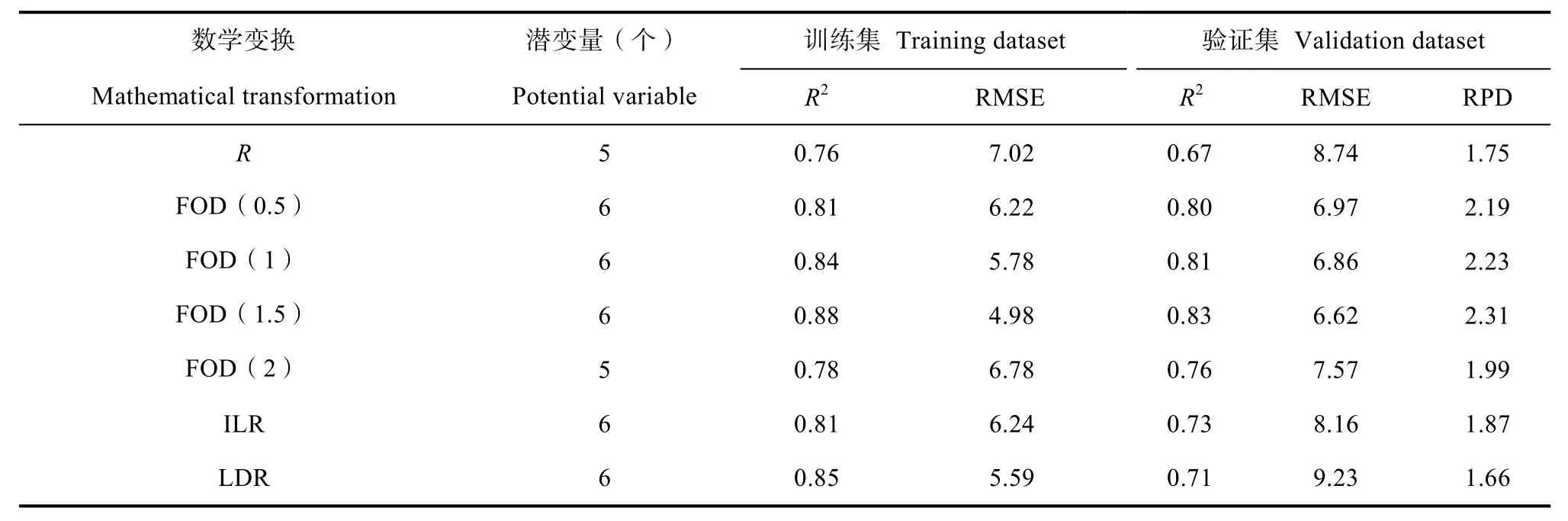
表1 红壤有机质含量PLSR 模型精度Table 1 Precision of the PLSR model in predicting red soil SOM content

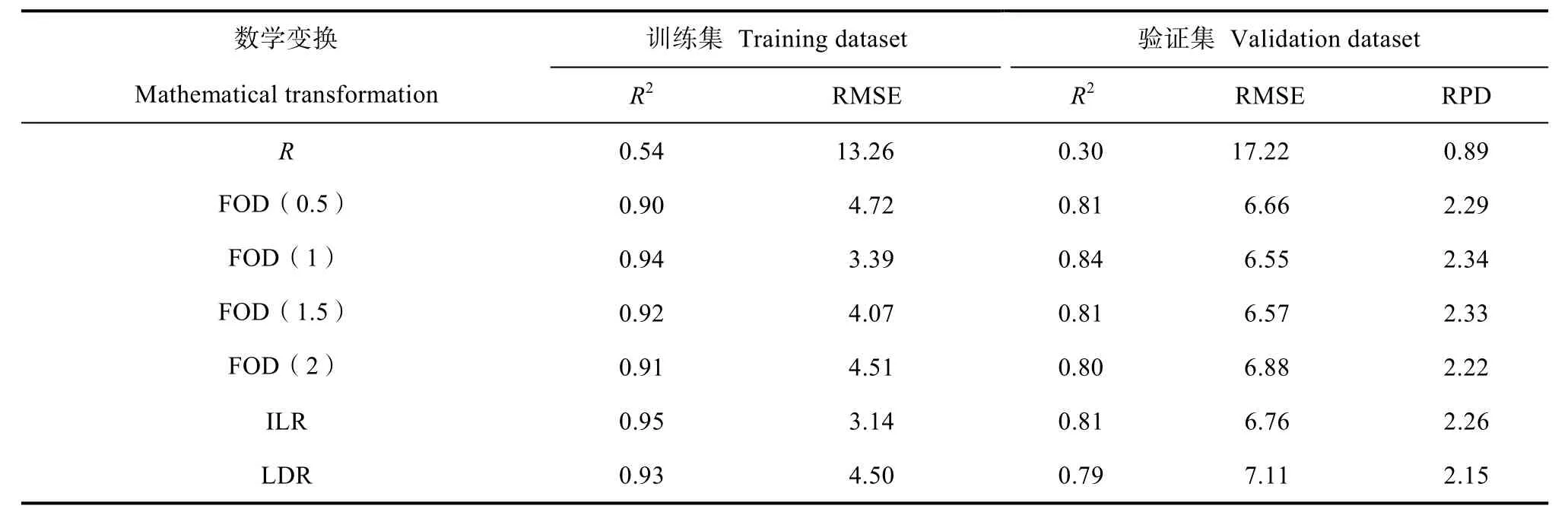
表2 红壤有机质含量BP 神经网络模型精度Table 2 Precision of the BP neural net model in predicting red soil SOM content

2.5 PLSR-BP 复合建模

在进行PLSR-BP 复合建模时，将PLSR 建模中提取出的潜变量作为自变量进行土壤有机质预测模型的构建。表3 为PLSR-BP 复合建模结果，与表1、表2 相比较，可以看出PLSR-BP 复合建模的R 模型RPD 较单一的PLSR 和BP 模型而言提升到了1.96，但仍只能对样本有机质含量进行粗略估测。ILR 模型的RPD 为1.98，较PLSR 建模提升了5.9%，但相比BP 神经网络降低了 12.5%，只能粗略估计样本有机质含量。FOD（0.5）、FOD（2）及LDR 模型的RPD分别为2.41、2.27、2.46，均具有较好的估测土壤有机质含量的能力。FOD（1）和 FOD（1.5）模型的RPD 分别为2.63 和2.75，具有很好的预测能力。除R 模型，其余模型训练集R2均低于BP 神经网络模型，验证集R2有所提升。其中FOD（1.5）优于0.5、1、2 阶导数模型，相比经过FOD（1.5）变换的BP 神经网络模型，训练集R2下降了 3.2%，RMSE 上升了15.0%，验证集R2上升了7.4%，RMSE 下降了 15.5%，RPD 上升了18.0%。图4 可以看出FOD（1.5）模型的验证样本基本在1︰1 线附近，预测能力为最优。总体而言，PLSR-BP 复合模型验证集的各项判定指标均优于PLSR 或BP 神经网络单独建模。

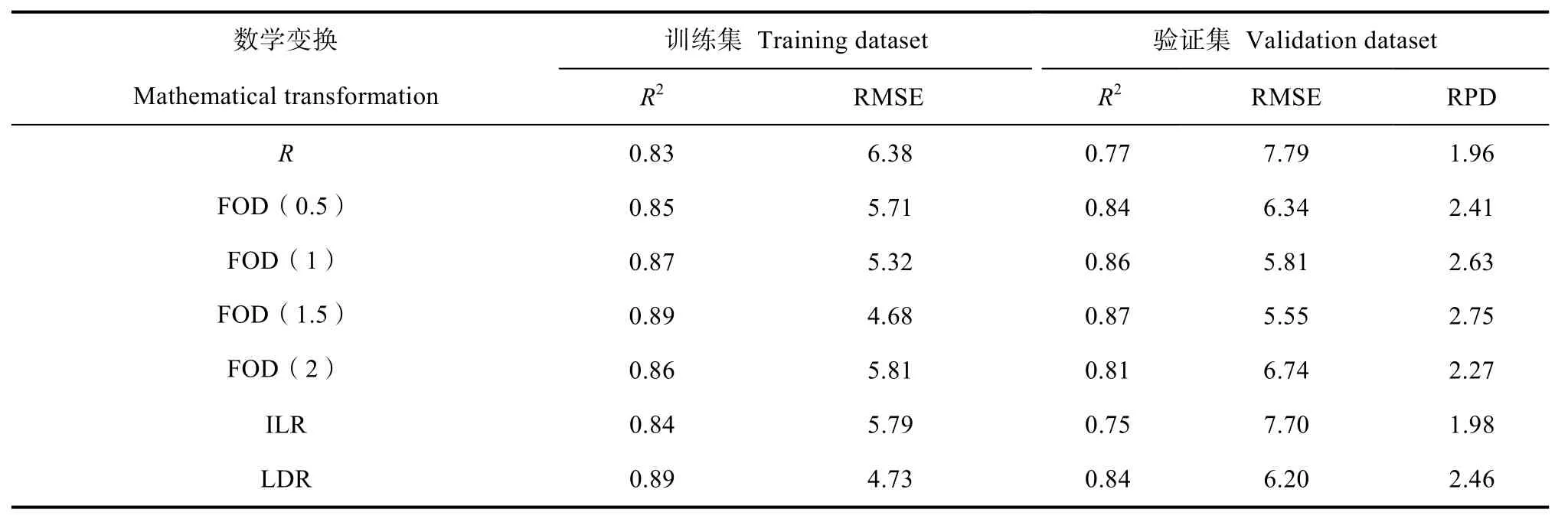
表3 红壤有机质含量PLSR-BP 模型精度Table 3 Precision of the PLSR-BP model in predicting red soil SOM content

图4 1.5 阶导数变换的有机质含量PLSR-BP 复合模型实测值与预测值比较Fig. 4 Comparison of measured SOM and the values predicted with the PLSR-BP model based on 1.5 order derivative transformation

3 讨 论

红壤氧化铁含量较高，主要是由于红壤在形成过程中的脱硅富铁铝化过程所造成的[31]。季耿善和徐彬彬[32]发现游离氧化铁在红壤光谱的 900 nm 附近吸收最强，对光谱特性的影响极大。而在对红壤有机质含量估测模型的构建中，刘磊等[33]通过对红壤原始光谱进行去包络线处理，使用其特征吸收带480～580 nm、820～950 nm、1 010～1 060 nm、1 360～1 500 nm、1 880～2 020 nm、2 160～2 240 nm进行有机质含量建模；谢文等[34]通过研究发现山地红壤有机质光谱特征波段位于600～2 450 nm 处，并选用全波段进行建模。他们在建立估测模型时均未考虑到氧化铁对于模型精度的影响。考虑到氧化铁在900 nm 左右的吸收谷的干扰，在波段选择上，本研究去除 801～1 000 nm 波段，选用 400～800 nm、1 001～2 450 nm 波段进行建模，以减小氧化铁对于有机质含量预测的干扰。

在土壤光谱数据建模前，对其进行各种数学变换是非常必要的，有助于构建精度更高的模型[35，36]。常用的数学变换主要有 1 阶导数、2 阶导数、倒数的对数等，本文在此基础上引入了目前研究较少的分数阶导数这一概念。分数阶导数的引入对整数阶导数的概念进行了扩展，在阶数的选择上更加广泛，同时也将隐含在光谱内的信息表现出来。张东[37]利用分数阶导数公式将0～2 阶的阶数间隔细化至0.1，发现在2 阶导数时模型的预测精度达到最优。本研究以0.5 为阶数间隔对土壤光谱数据进行0～2 阶的导数变换，经过导数变换后，发现采用PLSR 模型建模时模型的RPD，即预测能力FOD（1.5）＞ FOD（1）＞FOD（0.5）＞ FOD（2）；BP 神经网络建模时，各模型的RPD，FOD（1）＞ FOD（1.5）＞FOD（0.5）＞ FOD（2）；基于PLSR-BP 复合模型建模时的RPD，FOD（1.5）＞FOD（1）＞FOD（0.5）＞ FOD（2），与 PLSR 模型具有相同的趋势，即在0～2 的区间上对于有机质的预测能力呈现一个先升高后下降的趋势，在 1.5 阶导数时得到最优预测模型。BP 神经网络建模时，1阶导数变换得到了较好的预测模型可能是由于隐藏层神经元等参数设置不同而导致了该结果。与张东[37]研究结果不一致的原因可能在于土壤含盐量和有机质二者对土壤光谱的敏感性不同。

土壤光谱的近红外波段往往含有数据冗余，会增加建模的复杂性[38]。PLSR 模型能够很好地提取土壤光谱中的信息，同时使其与有机质含量的相关程度达到最大。文中非线性的 BP 神经网络模型较线性的 PLSR 模型有更好的预测能力，其不足之处在于 BP 神经网络训练集虽然有很高的决定系数，但由于输入变量过多，网络规模过大，影响收敛速度，造成了“过拟合”的现象，这也导致验证集与训练集精度相差较大。因此本文使用PLSR-BP 复合模型进行土壤有机质的预测，采用 PLSR 先对土壤光谱数据进行潜变量的提取，减少数据冗余，再对这些潜变量进行 BP 神经网络建模，这一方法可以有效避免使用单一的 BP 神经网络模型进行全波段拟合时出现共线性现象。结果表明，PLSR-BP 复合模型的 RPD 较单一模型高出了 0.12～1.07，说明PLSR-BP 复合模型在对红壤有机质含量的预测中的实用性。

本文不足之处在于仅构建了一个综合模型对林地、园地和水田三种土地利用类型的土壤有机质含量进行预测，而并未深入研究对于不同土地利用类型是否能采用同一模型进行土壤有机质含量的预测，这也是今后需要进一步研究的方向。

4 结 论

分数阶导数是在传统的整数阶导数上的扩展，减少了有用信息的遗漏，有助于土壤有机质含量的预测。对于使用经过分数阶导数变换的红壤光谱而言，在0～2 阶的区间上，对土壤有机质含量的预测能力呈现出先升高后下降的趋势，并在 1.5 阶处能够得到最优模型。在建模方法的选择上，偏最小二乘回归能够在保证土壤光谱与有机质含量相关性最大的基础上进行数据的压缩，减少数据冗余；BP 神经网络预测精度虽然较高，但由于输入变量过多易出现过拟合现象；偏最小二乘回归与 BP 神经网络结合可以综合二者的优点，提高模型的预测精度。