基于逐维判定的记忆减退布谷鸟搜索算法

刘紫阳 庞志华 郑韩飞 李丛萱 北华航天工业学院 计算机学院

引言

布谷鸟搜索算法（Cuckoo Search Algorithm，CSA）是一种模拟布谷鸟寄生育雏行为的仿生优化算法，其寻优能力来源于它的两个重要组成部分，一是基于莱维飞行（Lévy Flights）的随机游走过程，二是基于种群内部交叉变异的偏好随机游走过程。莱维飞行的随机步长来自于具有无限方差和无限均值的莱维分布，鸟巢位置采取强记忆性更新策略。强记忆性更新策略与盲目跳变的结合保证了最优解在进化中传递，避免了算法退化，但也会导致算法在当前解附进行多次无效开发，导致收敛速度过缓。

一些改进的CS 算法在一定程度上提升了CSA 的性能，但存在计算量大，引入更多外部参数等问题，面对高维复杂函数优化问题时难以兼顾全局探索与局部寻优性能。文献[5]提出逐维改进的布谷鸟搜索算法，通过降低随机游走的盲目性来提升搜索效率，但其莱维更新阶段仍使用强记忆更新策略，削弱了算法的全局探索能力，使算法容易陷入局部最优。

本文提出了基于逐维判定和记忆减退的布谷鸟搜索算法（Dimension by Dimension Decision Based Memory Loss Cuckoo Search Algorithm, DML-CSA）。MDL-CSA 在莱维更新阶段，采取无记忆策略，完全保留莱维飞行的更新结果。在偏好随机游走阶段采取逐维判定策略，逐个维度依次判断当前解在交叉变异后适应度是否降低（最小值问题），降低则接纳更新，否则保留原值。实验结果表明，两种策略的结合可以有效地提高CS 算法的收敛速度。

1 CS 算法

2 DML-CS 算法

2.1 逐维判定

结合式(4)和CS 算法的计算步骤可以看出，偏好随机游走是一种整体判定方式。对于多维目标函数，将解的各个维度进行种群间随机交叉变异后，再从整体评价本次更新是否提升解质量。然而，对于高维目标函数，每个维度的变化都会影响函数适应度，如果个别维度的退化覆盖了其他维度的进化，导致整个解的适应度退化，那么本次更新记为无效，不仅产生计算浪费。

DML-CS 算法采用逐维判定策略。在偏好随机游走阶段，从第一个维度开始依次执行如下操作：更新该维度值，评价更新对适应度的影响。如果更新使目标函数适应度降低则接纳该更新，否则保留原值。这是一种贪婪的更新方式，下一维度的更新在上一维度评价的基础上展开，每次更新都会提高解质量，从而加速了算法的收敛。

2.2 记忆减退策略

标准布谷鸟算法通过莱维飞行产生随机步长，如果随机步长的加入使得函数适应度降低则保留更新，否则保持原值。强记忆性的更新策略与跳变的盲目性的结合避免了算法退化，但同时削弱了莱维飞行的全局探索能力和局部挣脱能力，使算法容易在局部最优点处震荡。记忆减退策略则是直接将莱维飞行更新作为新解，不再对更新结果进行评判。这不仅减少了该环节对目标函数的评价次数，而且充分发挥莱维飞行的高随机性特点，使算法有能力跳出局部最优，找到全局最优值。

2.3 DML-CS 算法流程

DML-CS 算法步骤如下：

3 数值仿真与分析

将DML-CS 与标准布谷鸟算法CSA 和逐DDICS 算法[5]在多个具有典型特性的基准函数上进行测试，测试函数包含了2 个单峰函数（Sphere、Rosenbrock）和3 个多峰函数（Griewank、Alpine、Schaffer）。

3.1 实验参数

为使比较过程更公平，将3 种算法的共同参数设为一致（参见文献[5]），步长因子 ，发现概率 ，种群大 设为小为30，多维函数维数设为30，所有函数自变量变化范围设为[-100.00~,100.00]。

3.2 实验结果与分析

为直观展示DCS 算法寻优过程，图1~图5 展示了测试函数在3种算法下的适应度进化曲线，进化曲线采用半对数坐标，横坐标是目标函数的评价次数。目标函数评价是法迭代过程中占据计算资源对多的环节，横坐标采用评价次数可以直观比较3 种算法在消耗相同的计算资源情况下的寻优效果。

图1 Sphere 函数

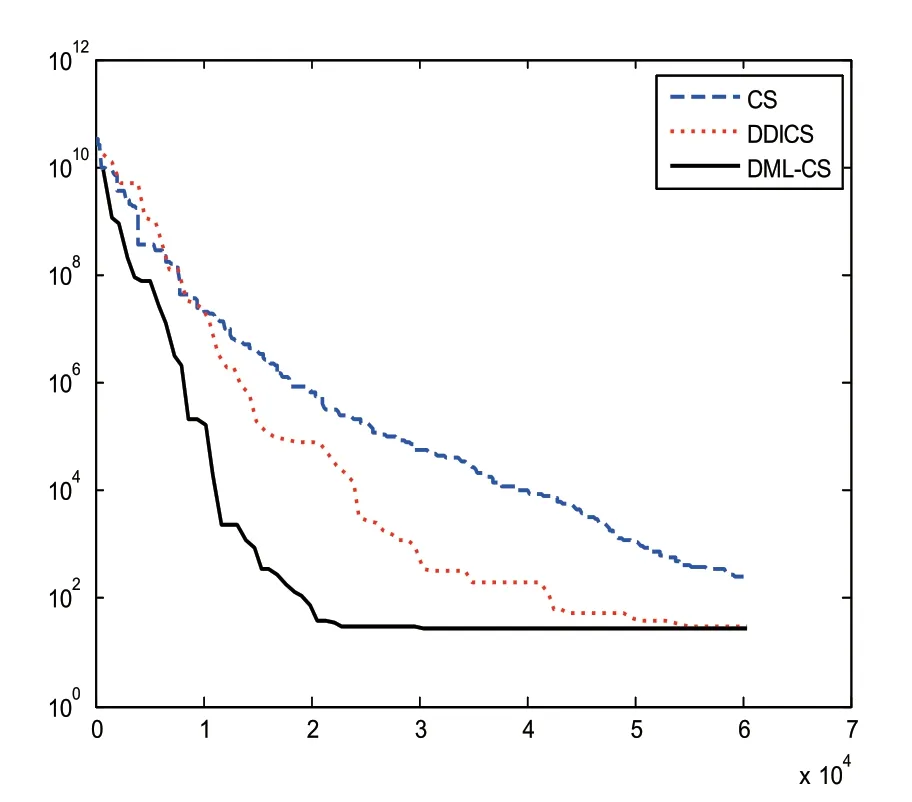
图2 Rosenbrock 函数

图3 Griewank 函数

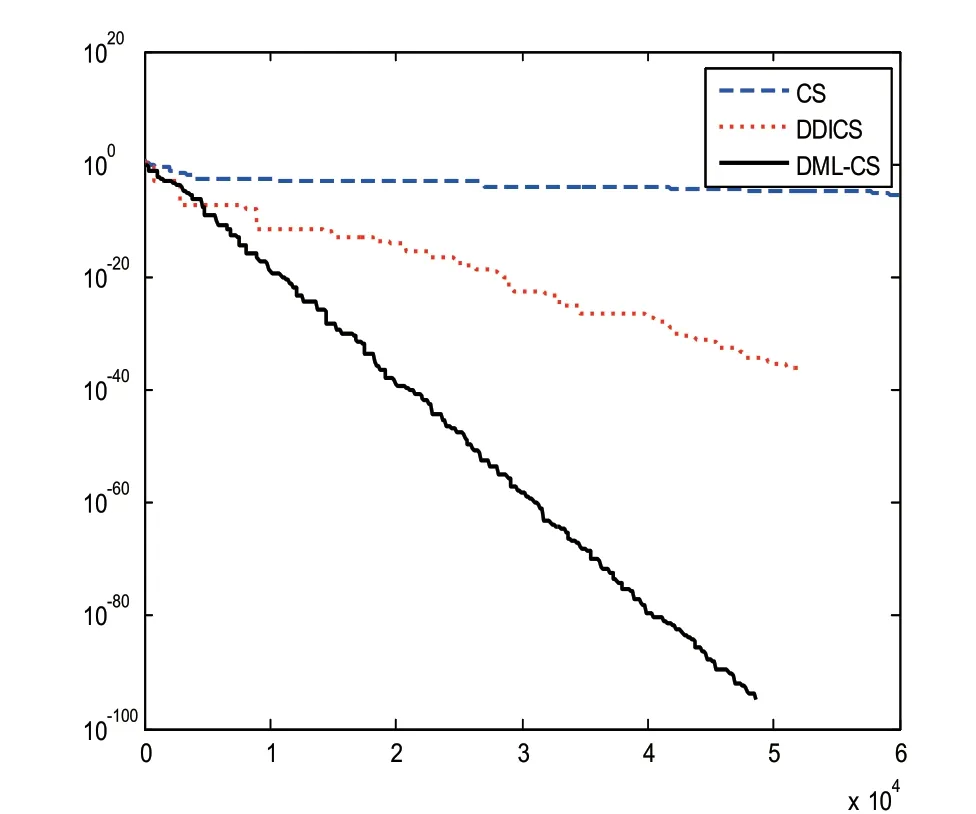
图4 Alpine 函数

可以看出，相较于标准布谷鸟算法，逐维改进的CS 算法的收敛速度在前期有了明显提升，但在迭代后期其收敛趋于缓慢，可能陷入局部极小值。而DML-CS 算法在整个寻优过程中都具有较快的收敛速度，随着迭代次数增长，DML-CS 算法适应度仍能保持较高的下降率。因此，在达到相同寻优精度条件下，DML-CS 算法所需时间更少。为了验证算法对低维函数的寻优能力，实验中引入了二维函数Schaffer 和Alpine。其中，Alpine 函数是一种经典的多模态最小化测试函数。当在定义域内趋于无穷大时，该函数沿着自变量方向会产生大量可微的局部极值，具有较高的寻优难度。图4 展示了Alpine函数在3 种算法下的适应度进化过程，CS 算法陷入局部最小值，寻优失败，DDICS 算法收敛较慢，DML-CS 算法经过3.0E+4 次评价就使误差达到了 10-20 级别，而为达到此精度，DDICS 算法所需的评价次数是DML-CS 的3 倍。由此表明，DML-CS 算法虽然针对的是高维函数的寻优问题，但它对低维函数同样有效。

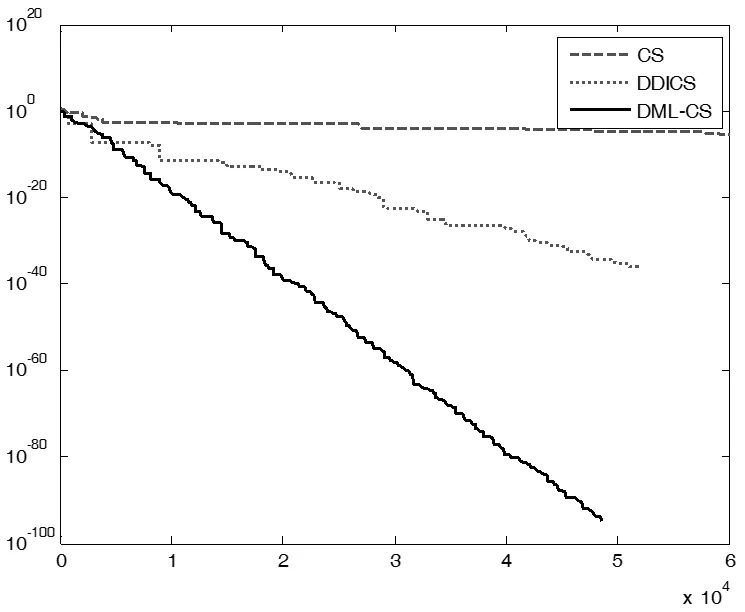
图5 Schaffer 函数

4 结语

解决高维函数优化问题时，CS 算法未能考虑不同维度间的相互干扰，强记忆更新策略又限制了莱维飞行随机步长的全局探索能力，导致算法收敛缓慢，容易陷入局部最优。本文提出了基于逐维判定和记忆减退的布谷鸟搜索算法，创新点有：

(1）莱维更新阶段，采取无记忆策略，充分发挥了莱维飞行步长的随机性，使算法有较强的全局探索能力和局部最优挣脱能力。

(2）偏好随机游走阶段采取逐维判定策略，逐维度判断当前解在交叉变异后适应度是否降低，减少了解的各个维度间的相互干扰，降低随机游走的盲目性，提升算法收敛速度。

DML-CS 算法与CS 算法和DDICS 算法的对比试验结果表明，DML-CS 算法不仅能在多维函数上取得较好的寻优效果，在低维函数上的表现同样优异，并且DML-CS 算法对多峰函数和单峰函数的优化效果同样优于对比算法。因此，DML-CS 算法是一种更有竞争力的算法。