基于飞蛾扑火算法的自移式排岩机轻量化设计

李 光，孙 刚，乔建强，张永明，杨 佐，宋学官

(1.太原重工股份有限公司 技术中心， 山西 太原 030024；2.大连理工大学 机械工程学院 ，辽宁 大连 116024)

0 引言

大型露天矿自移式排岩机是一款广泛应用于露天矿连续/半连续开采生产的复杂工程机械，是保障国家能源供给和资源开采急需的重大技术装备。由于排岩机的技术含量高，关键技术长期以来被德国和瑞典垄断，使我国复杂的重大装备技术发展相对迟缓。在太原重工的努力下，自主研制出了大型露天矿自移式排岩成套装备，并在太钢集团和包钢集团得以应用，取得了良好的效果。虽然太原重工已成功研制出大型露天矿自移式排岩机，但在设计初期仅考虑了系统的制造成本，未考虑排岩机的自重因素。为提高其性能并降低排岩机的自重，在保证满足排岩机强度的使用要求下，本文利用飞蛾扑火优化算法对排岩机上部工作装置进行轻量化研究，获得了最佳的参数配置关系。

1 排岩机的系统组成与改进

排岩机是一款集成了多个学科的复杂装备，其主要作用是将卸料车送过来的物料通过排料臂进行排放，调整回转角度与俯仰角度可使落料点的位置及落差发生变化，满足实际的排料需要[1]。排岩机系统通常是由履带行走机构、回转机构、排料臂、俯仰机构、受料臂和配重臂等组成，如图1所示。

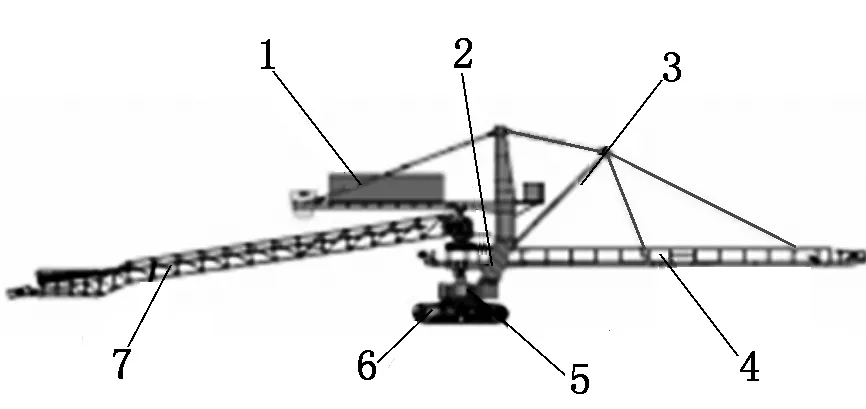
1-配重臂；2-俯仰机构；3-拉杆；4-排料臂；5-回转机构；6-行走机构；7-受料臂

当前排岩机的结构布局通常是借鉴国外并进行类似设计的，虽然图1中的排岩机布局结构具有适用性强、生产效率高、故障率低、输送能力大等诸多优点，但仍存着自重大(工作重量超过1 000 t)、露天工作风载大、颗粒运输量大的缺点。通过分析排岩装备的结构参数、排岩机的性能指标以及物料排放工艺参数，设计了一种新型的结构布局方案，彻底改变了传统排岩机基于经验公式和类似设计的不足。新型的排岩机结构布局方案如图2所示。

图2 改进后的排岩机结构示意图

通过实验测试对比，改进前的排岩机结构重心较高，设备上部迎风面积大，倾覆力矩大。改进后的排岩机结构相对改进前重心高度降低了32.6%，同等条件下倾覆力矩仅1 203 kN·m，降低了19.8%。改进后的结构可以满足九级烈风下的安全平稳运行。

2 飞蛾扑火算法原理

飞蛾扑火优化(moth-flame optimization, MFO)[2-3]算法是澳大利亚格里菲斯大学Mirjalili学者基于生物学原理提出的一种新型群智能优化算法，该算法主要是通过模拟飞蛾在夜间横向定位的飞行方式进行寻优的。在MFO算法中，飞蛾的集合为M，可以表示为：

(1)

其中：Mij为第i个飞蛾对应的第j个位置。假设火焰的集合为F，Fij为第i个火焰对应的第j个位置，则火焰集合可以表示为：

(2)

为了方便对飞蛾扑火优化算法进行数学建模，假设每只飞蛾的位置可以按照式(3)进行更新：

Mi=S(Mi，Fi).

(3)

其中：Mi为第i个飞蛾；Fi为第i个火焰；S为螺旋函数。

飞蛾的飞行路径可以定义为：

S(Mi，Fj)=Di·ebt·cos(2πt)+Fj.

(4)

其中：Di为第i个飞蛾和第j个火焰之间的直线距离；b为定义的螺旋线形状常数；t为随机数，取值范围为[-1,1]。

由公式(4)可知，当t在[-1,1]之间取随机数时，距离飞蛾最近位置的火焰被更新到的概率就越大，很容易使得飞蛾陷入局部最优解，而搜索不到全局最优解。为避免飞蛾陷入局部最优，同时还能够以最快的速度获得全局最优并降低寻优时间，因此，火焰的数量会根据运行的代数而减少，该函数可以描述为：

(5)

其中：l为当前迭代的代数；N为最大的火焰数目；T为最大的迭代次数。MFO算法的流程如下：

(1) 初始化飞蛾种群，并计算初始飞蛾种群的适应度值。

(2) 对适应度值进行排序，并计算火焰位置和其适应度值。

(3) 根据公式(5)计算出飞蛾的数量并删除末尾的飞蛾和火焰。

(4) 计算飞蛾和对应火焰之间的直线距离并将其代入公式(4)，获得更新后飞蛾值。

(5) 根据更新后的飞蛾种群计算出适应度值。

(6) 判断是否得到终止条件，否则跳转到(2)循环计算。

3 排岩机的轻量化优化设计

3.1 优化模型的建立

为保证优化后的结构仍能够满足工作条件的要求，在对排岩机进行优化时，需要使受料臂和排料臂的长度不变。结合排岩机的系统组成可知，排岩机的结构是一个典型桁架结构且属于对称形式分布[4-5]，故可以将其简化为平面杆系结构。本文在对排岩机进行轻量化研究时，其设计变量主要选取排料臂主梁面积x1、配重臂距离地面的高度x2、配重臂主梁的面积x3和受料臂主梁面积x4，各个变量在排岩机中的相对位置如图3所示。

排岩机的优化目标是系统的自重最小，在对排岩机进行优化时，各个杆件受到的最大应力均需不大于材料的屈服应力。因此排岩机的优化模型可以表示为：

(6)

其中：M0为行走机构和配重块等附件的重量；ρ为材料密度；Ak为各段主梁的面积；lk为各段主梁的长度；σmin、σmax和σk分别为杆件的最小应力、最大应力和实际应力。

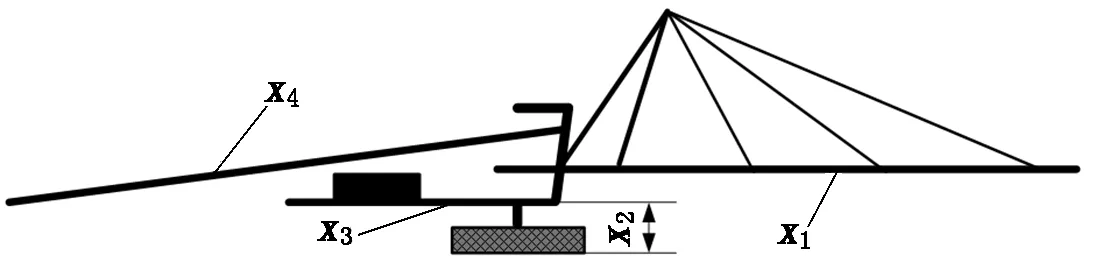
图3 排岩机等效模型

3.2 优化结果分析

通过运用MFO算法对排岩机的模型进行优化，优化后的结果如表1所示，其中Mmean、Mworst和Mbest分别表示中间值、最劣值和最优值。

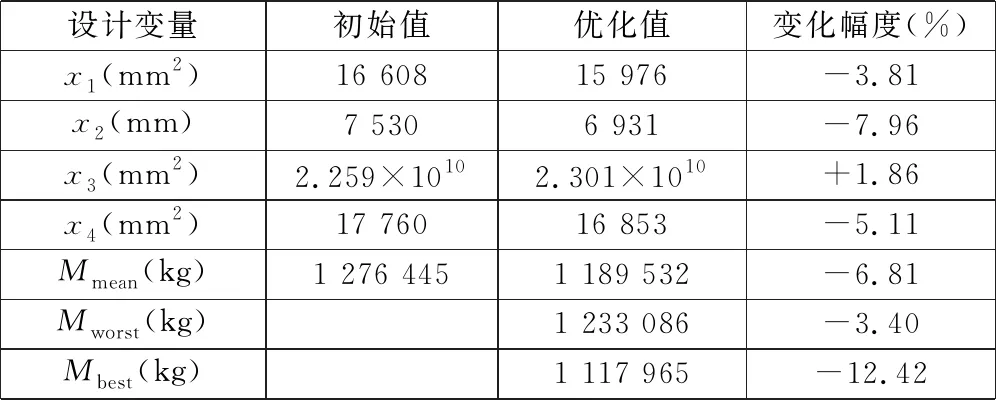
表1 排岩机优化结果

由表1中的结果可知：除了配重臂的横截面积增大外，其余变量均相对初始值有所减小，变化幅度最大的为配重臂的高度，由初始值的7 530 mm降低为6 931 mm，变化幅度为7.96%。对比优化前、后的变化可知，最优化排岩机的重量最小为1 117 965 kg，相对优化前降低了12.42%。排岩机的优化迭代图如图4所示。

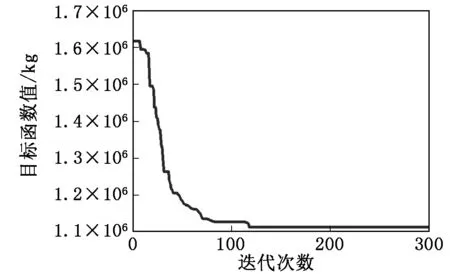
图4 目标函数迭代图

由图4可知：在MFO算法的优化下，目标函数迅速向全局最优解靠拢，在第119代迭代后目标函数达到稳定解，其值为1 117 965 kg。

4 结论

通过分析当前排岩机存在的不足，设计了一种新型的结构布局方案，运用飞蛾扑火优化算法对排岩机进行了轻量化研究，结果表明最优化排岩机的重量由1 276 445 kg降低为1 117 965 kg，降低了12.42%。通过对排岩机进行优化设计，对今后的结构改进和性能优化具有参考意义。