玻璃钢复合材料板材Lamb波传播特性分析
2020-06-22齐添添何才厚王海涛黄丽霞李秋锋
齐添添, 陈 尧, 何才厚,2, 王海涛, 黄丽霞, 李秋锋
(1.南昌航空大学无损检测技术教育部重点实验室,南昌330063;2.江西省特种设备检验检测研究院鹰潭分院,江西鹰潭335000;3.中国建筑建一局集团第二建筑有限公司,北京100161)
0 引 言
作为一种有效的超声检测技术,超声Lamb 波在板材无损检测与评价中的应用非常广泛[1-3]。而在玻璃钢复合板材检测中,由于该玻璃纤维增强塑料是由纤维、基体、界面组成,其微观构造是一个复杂的多相体系,在检测时发现声速不均匀且各向异性较强。因其具有轻质高强等特点在国防和航空航天上应用广泛,因此对其进行有效无损检测具有重大的研究意义[4-7]。
目前对玻璃钢复合材料中超声波传播特性进行系统分析的研究不多,刘磨等[8]利用一次底波法进行玻璃钢容器厚度的测量,采用一次底波法是因为玻璃钢复合材料的衰减较大,同时表明超声检测是复合材料的重要检测方法之一。唐军君等[9]绘制碳纤维复合材料频散曲线,探究不同模态Lamb 波的衰减特性进行故障诊断。马波等[10]通过短波实验分析了声发射信号在玻璃钢复合材料板中的衰减规律和传播速度规律,并对波速进行线性定位。这些研究只是通过实验从信号分析角度对特定结构检测中发现了一些检测规律,具有一定的局限性。有限元技术是分析应力波的有效方法,也是分析超声波传播过程中的应力、应变情况的有效工具[11-14]。李伟等[15]采用脉冲发射法并用有限元软件模拟超声波在复合材料中的传播特性,得到了A 扫波形图,依据回波信号的幅值可以判断缺陷的大小和通过回波信号的到达时间可以判断缺陷的所在位置;陈亮等[16]采用基于有限元方法计算薄板超声Lamb波频散曲线,结果表明频散曲线与通过频率特征方程求解的超声Lamb波理论频散曲线相吻合。本文采用ABAQUS有限元模拟方法开展系统性的研究,建立了铺层角度为[0°/90°]和[±53°]的两种玻璃钢复合材料模型,在层压板距中心点60 mm处不同方向的信号接收点,建立了铺层厚度为3、6 和9 mm 的玻璃钢复合材料模型,以及200、300 和400 kHz 激励信号对玻璃钢复合材料进行衰减特性、声速传播和纤维铺层角度关系的研究。
1 波的传播特性及原理
弹性波在各向异性材料中传播的波动方程位移表示形式[17]:
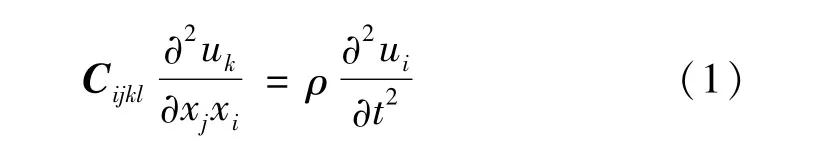
式中:Cijkl为弹性矩阵;xi为坐标系;ui为位移(i,j,k,l=1,2,3)。
质点在平衡位置的简谐振动为

式中:um为振动幅值;ω为角频率。
由式(1)和(2)得各向异性材料的本征方程:

式中:ρ为材料密度;δim为克罗内克符号;k为波数。
利用有限元仿真方法求解自由振动方程,可将上式简化为求解特征方程:

因本文分析超声波在复合材料层压板中的传播,因此需考虑边界条件:
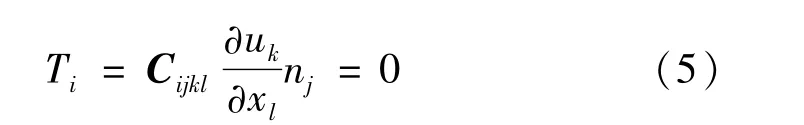
式中:nj为边界单位外法向量n的轴向分量。
根据Bloch-Floquet定理求解为:

式中:k =[kx,ky,kz]T为Bloch波矢;uk(r)为具有空间周琦的函数,
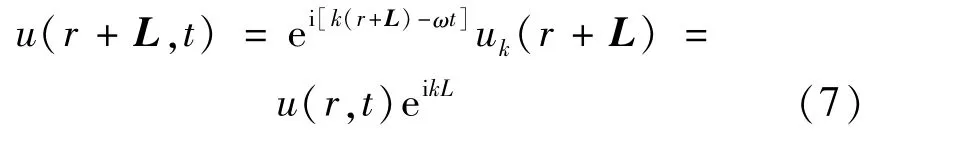
L为晶格平移矢量。
当一超声导波在复合材料中传播,在板内传播受到板结构的上下边界条件的约束时,在上下界面发生多次反射、折射和波形转换导致各种模态的波形混叠而形成的导波随频率的变化声速随之改变,称之为频散现象。
板波按传播方式可分为对称型板波(S型)和反对称型板波(A型)两种,超声Lamb 波波速与频率f、板厚b的关系如下:
对称型(S型)

反对称型(A型)

式中:f为声波频率;b为板厚;ktl为无限大介质中纵波声速;kts为无限大介质中横波声速;vp为Lamb 波的相速度。
基于频散原理可得,频率和厚度会对声速传播和衰减有很大影响,但反映频率和厚度对频散比较严重的玻璃钢复合材料的声学传播变化的资料较少,因此了解波在玻璃钢复合材料板中的传播对后续实验及实际应用有很大帮助。图1 为Disperse 软件得到的玻璃钢复合材料群速度频散曲线。
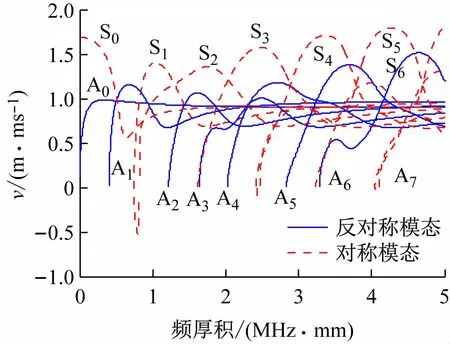
图1 玻璃钢复合材料群速度频散曲线
当一激励加载到玻璃钢板上时,在接收点接收到的信号是多个模态兰姆波的叠加,不利于对传播特性的研究。因此,根据玻璃钢复合材料属性绘制频散曲线,可看出随着频率、厚度(频厚积)增大模态增多,当频厚积为1.6 MHz·mm以下时,仅有A0、S0和A1模态;当频厚积在1.6 ~4.3 MHz·mm 时,模态有8 个;当频厚积增大,模态迅速增多,会降低准确性,为研究增加了难度。为了解Lamb 波在各向异性板中的传播情况,本文依据频散曲线可看出由于A0模态没有截止频率且较平稳,因此本文采用斜入射法激发A0模态Lamb波。为激发单一模态A0兰姆波,需符合Snell定律,即sin α =cl/cp,得到相应频率下的斜入射的激发角度。cl为声波在空气中传播速度;cp为不同厚度板材时对应频率下A0模态Lamb的相速度。
本文采用单一变量法探究各不同影响因素对声波传播的变化规律,采用[0°/90°]和[±53°]两种铺层角度的玻璃钢层压板模型,激发频率变量为200、300和400 kHz,板材厚度为3、6 和9 mm,采用单一变量法对玻璃钢复合材料层压板模型进行对比。
2 有限元模型建立
图2 玻璃钢复合材料模型
复合材料的铺层角度不同对材料性能的影响很大,因此本文建立[0°/90°]6和[±53°]6两种铺层角度的玻璃钢层压板模型建立,如图3 所示,以比较不同铺层角度的玻璃钢材料对超声波传播特性的影响。
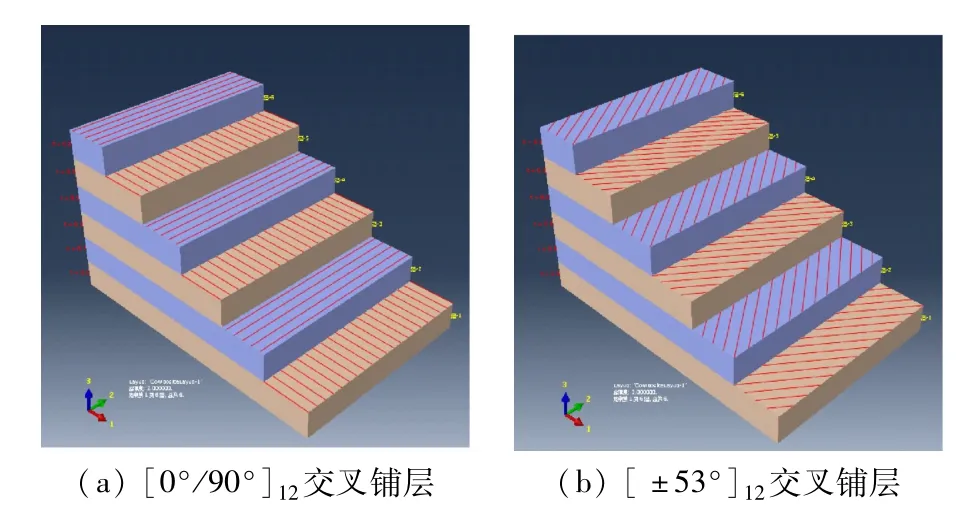
图3 玻璃钢复合材料交叉铺层示意图
由于划分网格单元尺寸的大小对仿真结果有直接影响,本文中仿真模型选用网格单元为1 mm 的四节点曲面四边形(S4R)。激励信号位置为玻璃钢复合材料层压板的中心点,分别在距激励点60 mm的不同方向设置接收点,如图4 所示,为复合材料的纤维方向和非纤维方向,进而分析A0模态Lamb 波在不同方向上的声学传播特性。
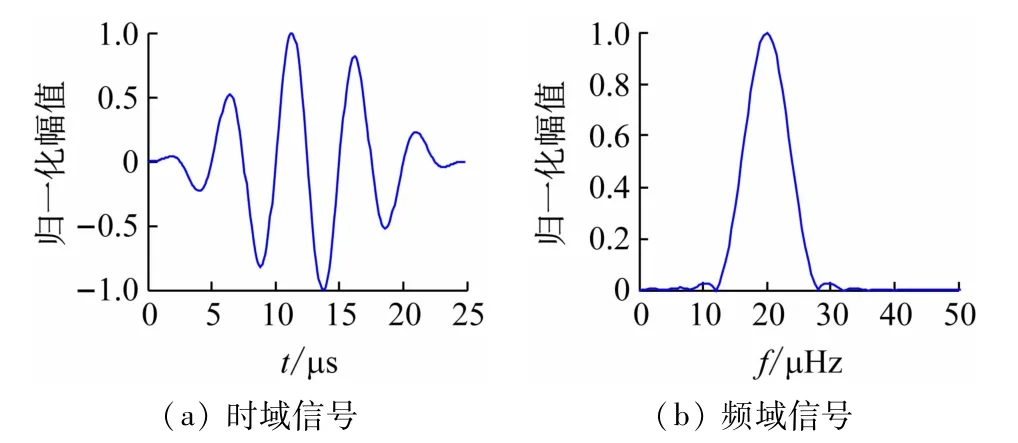
图4 不同方向接收点示意图
本文采用动态/显示程序类型,时间长度为0.02 ms。里程输出中,作用域作用于各个方向接收点,频率为每个x个,时间单位为0.33 μs,由于本文研究声学传播特性,因此选用位移/速度/加速度-U,平移和转动作为输出变量。
3 仿真测试与结果分析
3.1 玻璃钢复合材料超声波传播特性数值仿真
在建立模型的过程中,铺层角度设置为[0°/90°]6交替铺层和[±53°]6交替铺层两种不同铺层方式,层压板厚度为3 mm,激励中心频率为200 kHz,入射角度23°,激励信号时频图如图5 所示。仿真结果得到声波在各点的接收时间-位移图,如图6 所示为铺层角度[0°/90°]6板厚3 mm 激励频率300 kHz模型0°接收点的历程输出图。仿真结果得到玻璃钢复合材料板Lamb波传播应力云图,如图7 所示。
根据公式

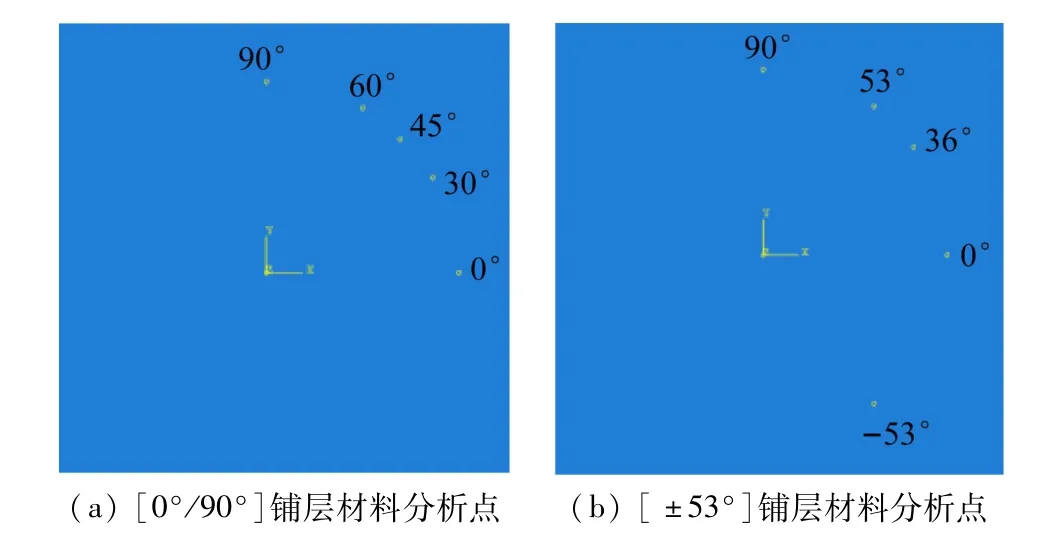
图5 中心频率为200 kHz的激励信号

图6 00 方向的历程输出图

图7 玻璃钢复合材料板应力云图
可以计算出超声波在各个方向上的传播声速和根据历程输出图始波波峰的波动,可以看出超声波在各个方向上的衰减情况。式中:C 为声速;S 是接收点和激励点之间的距离;t1是激励信号峰值所对应的时间;t2是接收点历程输出图始波波峰所对应的时间。
由表1 中不同铺层角度的实验结果分析可知,当铺层角度为[0°/90°]时,0°和90°方向声速比另3 个方向声速大,当铺层角度为[±53°]时,53°和-53°方向比其他方向声速大,0°、90°、53°和-53°分别为复合材料仿真模拟的纤维方向。由图7 也可见,Lamb波在纤维方向传播较快,且能量较高,衰减较小。初步判定,纤维方向的声速比非纤维方向声速大;且铺层角度为[0°/90°]的材料关于45°角对称。
3.2 不同方向的数值仿真的结果及分析
为验证3.1 节初步判定纤维方向声速大于非纤维方向声速的结论并非偶然,探究不同方向接收点超声波传播特性的影响,模型铺层方式为[0°/90°],频厚积为0.6、0.9 和1.2 MHz·mm,进行有限元仿真。
(1)管理理念的差异.由于不同国家的社会文化不同,受到的地域文化影响不同,各国企业的管理理念有很大差异.如中西方企业在管理中的差异,使企业在推行企业文化、制定企业战略过程中形成较大的文化冲突.
由图8 和表2 可看出,0°和90°是模型的纤维方向,纤维方向接收点的声速明显大于非纤维方向接收点的,45°方向声速最小,呈现“V”字型现象,沿着非纤维方向的衰减比纤维方向衰减大,且有对称现象,沿45°对角线对称。

表1 不同铺层角度的实验结果

图8 不同方向接收点的声速
3.3 频厚积对复合材料超声波传播特性数值仿真
由于玻璃钢复合材料具有各向异性,且会产生频散效应,模态较多,采用A0模态Lamb 波探究频厚积对传播特性的影响。由频散曲线可看出,虽然A0模态没有截止频率,但频厚积在0 ~0.5 MHz·mm 时群速度线性突增,不利于进行试验;在0.6 MHz·mm 时声速处于最大值然后缓慢下降趋于平稳。因此本文只探讨频厚积0. 6 ~2. 7 MHz·mm,模型铺层方式为[0°/90°],进行有限元仿真,得出声速见表3,并绘制折线见图9。
由图9 可看出,随频厚积的增大,各个方向接收点的声速均为下降且趋于稳定的,这与频散曲线A0模态吻合。本次实验采用的频厚积为0.6 ~2.7 MHz·mm,频厚积从0. 6 MHz·mm 最大值开始下降,1. 2 MHz·mm时趋于平稳,至本次实验最大频厚积2. 7 MHz·mm时声速在1.1 km/s左右,浮动较小,但非频厚积越大越好。且由图10 可看出,当频厚积在2.7 MHz·mm时,始波与反射波叠加,随频厚积继续增大,达到其他模态的截止频率时,会出现模态转换,影响实验准确性。因此当频厚积在0.6 ~1.8 MHz·mm范围内为实验的最佳频厚积区间。
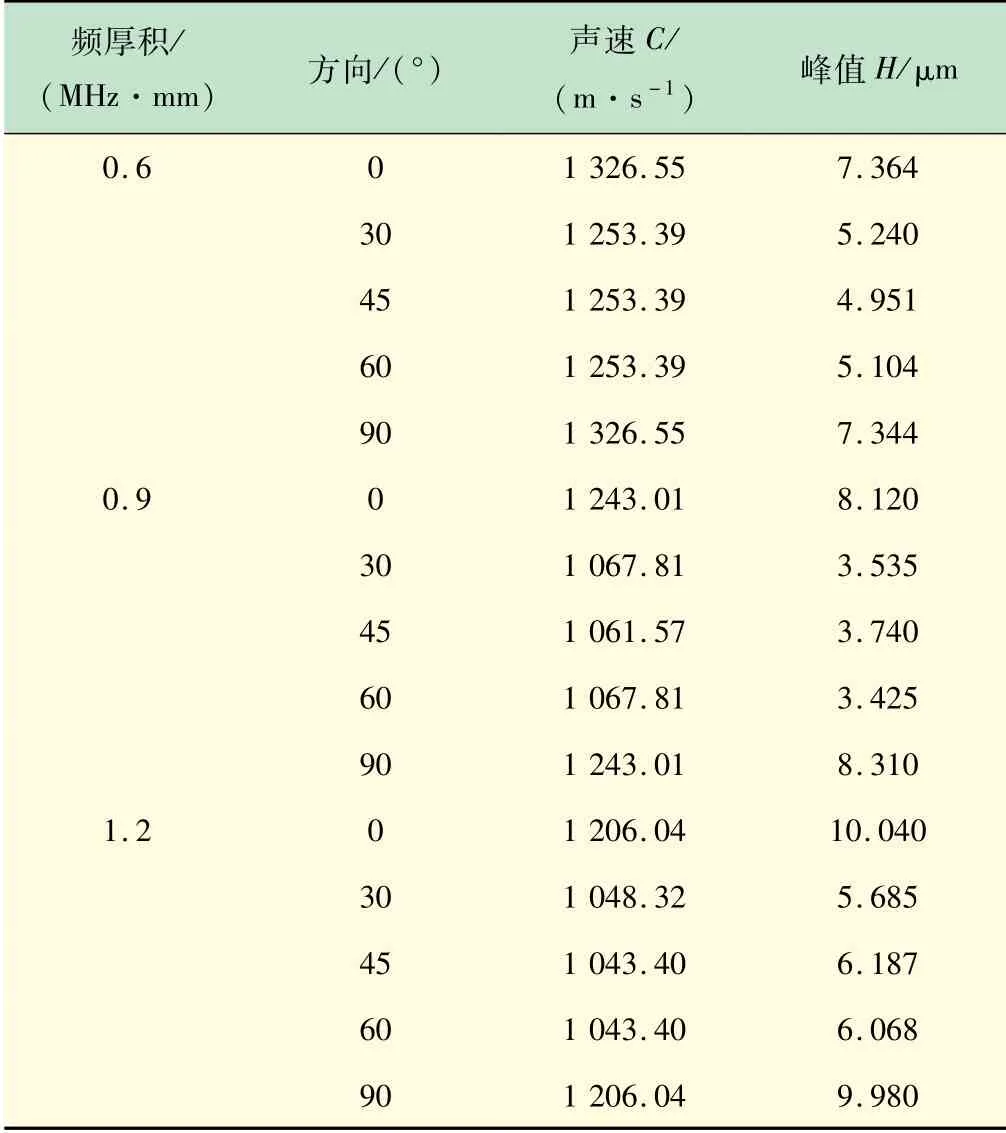
表2 不同方向的数值仿真结果

表3 不同方向的声速计算结果 m/s

图9 频厚积-声速关系

图10 2.7 MHz·mm时0°方向的历程输出图
4 结 论
本文通过建立玻璃钢复合材料层压板仿真模型,得出以下结论:
(1)对于不同的铺层角度构建的复合材料,超声波的传播特性差异较大,声速在铺层方向即纤维方向传播速度较快,而在非纤维方向传播速度慢,且衰减快。
(2)对于超声波在玻璃钢复合材料的不同方向上接收点的传播特性,本文分别设定0°、30°、45°、60°、90°方向分析点,其中是0°、90°纤维方向,其他方向为非纤维方向,实验表明,纤维方向的传播声速明显比非纤维方向的传播声速大,且声速呈现一定的对称现象。
(3)对于不同频厚积的材料,当激发A0模态Lamb波时,随频厚积增大,声速呈下降并逐渐平缓稳定现象,且没有其他模态Lamb 波出现,得出频厚积在0.6 ~1.8 MHz·mm范围内进行试验较合理。
