空调房数学建模与仿真

郭安柱 马永志

（青岛大学机电工程学院，山东 青岛266071）

1 概述

随着我国经济的快速发展，人民生活水平也在不断提高，空调已经是家家户户必备的产品。众所周知，空调房系统是一个具有高度的非线性、滞后性的复杂系统[1]，房间温度受到各种因素的影响，各种因素对房间温度的影响程度不一，为了探究外界因素对房间温度的影响，更好的通过空调系统对房间温度进行调节，利用集总参数法建立了空调房系统的动态数学模型，采用Matlab/Simulink 对系统进行模拟仿真。

2 模型建立

2.1 物理模型的建立

文章物理模型的原型为青岛某一办公室，其室内结构布局如图1 所示，办公区被分隔为三部分，整个办公区长6.2m，宽4m，高3m。整个办公区采用全空气空调系统，送风形式为侧送风。

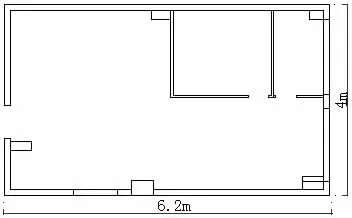
图1 青岛某办公室平面结构图

2.2 数学模型的建立

空调房为一个非常复杂的热力学系统，具有惯性大、影响因素多、高度的非线性等特点[1]，想要准确的描述其热力学特征非常困难，为了方便建模和求解，本文在实际的空调房热力学模型的基础上提出了以下假设[2]：

（1）房间温度场分布均匀，即房间各个点的温度一样；

（2）不考虑房间中其他因素对温度场的影响，仅考虑几个主要的热源；

（3）与室内进行热交换的围护结构主要为墙体，不考虑其他结构如窗户等对室内温度的影响且室内无阳光直接照射；

空调房空气温度对象建模：

根据能量守恒定律，空调房内空气储热量的变化率等于单位时间内空调房得到的能量减去空调房失去的能量[3]，则空调房能量守恒的计算公式为：

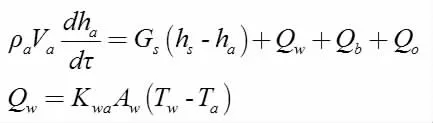
式中，hs为空调房送风焓值，J/Kg；ha为空调房空气焓值，J/Kg；ρa为空气密度，Kg/m3；Va为空调房室内空气体积，m3；Gs为送风量，Kg/s；Qw为室内围护结构与空气的对流换热量，W；Qb为空调房内人体与空气之间的换热量，W；Qo为室内其他热源如电灯和电子设备的产热量，W；Kwa为墙体与空气之间的对流传热系数，W/（m2·K）；Ab为墙体与室内空气之间的对流换热面积，m2；Tw与Ta分别为墙体内表面与室内空气温度，K；τ 为时间，s；

人体与空气之间的换热量由三部分组成，分别是人体通过呼吸作用、辐射作用和自然对流与空气之间的换热量。

①人体呼吸作用

人体通过呼吸作用与空气进行热湿交换，呼吸热损失包括显热热损和潜热热损两部分[4]，呼吸热损失的计算公式为：

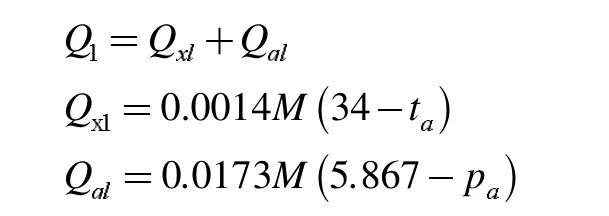
式中，Q1、Qxl和Qq1分别为呼吸热损失，显热热损失和潜热热损失，W/m2；M 为人体新陈代谢代谢速率，W/m2；pa为室内水蒸气分压力，kPa；

人体呼吸速率的计算公式为：

上式中，Gb为人体呼吸速率，Kg/s；Cb为计算常数，1.43×10-6Kg/J；

由此人体与室内空气之间由呼吸引起的热交换量为：

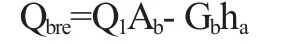
其中，Qbre为人体与室内空气之间由呼吸引起的热交换量，W；

②辐射传热

人体外表面与空调房围护结构之间的辐射换热量为：

式中，Qr为人体外表面与空调房围护结构之间的辐射换热量，W；Ab为人体外表面积，m2；σ 为斯忒藩一玻耳兹曼常量，5.67×10-8W/（m2·K4）；T1为人体外表面温度，K；Zb为人体质量，Kg；Hb为人体高度，m；

③对流传热

人体与空气之间对流传热量的计算公式为[5]：

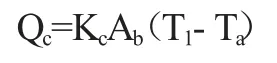
式中，Qc为人体与空气之间的对流换热量，W；Kc为人体与空气之间的表面对流换热系数，W/（m2·K）；

其中，表面对流传热系数Kc的计算公式为：

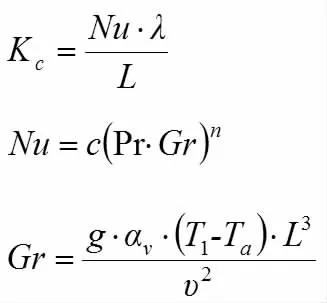
式中：

Nu 为努塞尔数；λ 为空气的导热系数，W/（m·K）；L 为特征长度，此处取人体身高，m；c，n 为计算常数，分别取0.1，033；Pr和Gr 分别为空气的普朗特数和格拉晓夫数；g 为重力加速度，m/s2；αv为空气体积膨胀系数，K-1；υ 为空气运动粘度，m2/s；

围护结构温度对象建模：

不考虑潜热交换的条件下墙体外表面和室外环境之间的换热量Qwo为[6]：

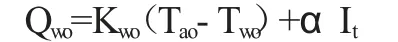
式中，ρw为墙体密度，Kg/m3；Vw为墙体体积，m3；hw为墙体焓值，J/Kg；Aw为墙体表面积，m2；ΔQc为内外墙体导热换热量，W；λw，墙体导热系数，W/（m·k）；δw，墙体厚度，m；α 为墙体对太阳辐射吸收比；

其中，倾斜面太阳辐射强度It和室外空气综合温度Tao的计算如下：

（1）倾斜面太阳辐射强度[7]

倾斜面总的辐照度：

It=Ibt+Idt+Irt

水平面总辐照度（测量得出）：

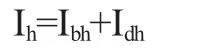
上式中：It为倾斜面总辐照度，W/m2；Ibt为倾斜面直射辐照度，W/m2；Ibh为水平面直射辐照度，W/m2；Idt为倾斜面散射辐照度，W/m2；Irt为倾斜面反射辐照度，W/m2；Ih为水平面总辐照度，W/m2；Ibh为水平面直射辐照度，W/m2；Idh为水平面散射辐射度，W/m2

倾斜面直射辐照度：

上式中，φ 为当地地理纬度；β 为集热器倾斜角；δ 为赤纬角；ω 为时角

倾斜面反射辐照度：

Irt=Ihρ（1-cosβ）/2

上式中，ρ 为地面反射率，普通地面取0.2，积雪时取0.7

倾斜面散射辐照度：

Idt=Idhρ（1+cosβ）/2

（2）室外空气综合温度

室外空气综合温度是一个全面性指标[8]，它包含了室外空气以及太阳辐射强度等方面的影响，因为其受太阳辐照度影响巨大，室外空气综合温度与太阳辐照度呈现相近的变化规律，在24h 内近似表示为呈周期变化的三角函数。室外空气综合温度的计算公式[9]：

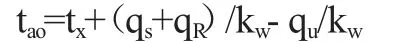
式中：tx为室外空气温度，℃；qs和qR分别为为围护结构外表面所吸收的太阳辐射热量和围护结构外表面所吸收的地面反射辐射热量，W/m2；kw为外墙总表面换热系数，W/（m2·K）；qu为夜间辐射，W/m2。

3 模拟结果

文中用Matlab/Simulink 建立了相应的计算机仿真系统，在进行仿真计算之前，首先需要确定系统运行的初始条件：室内温度ta=25℃，送风温度ts=20℃，送风量Gs=0.33Kg/s，太阳辐射强度I=450W/m2，墙体内表面温度tw=24.4℃，室外温度taout=30℃。仿真系统模型如图2 所示。

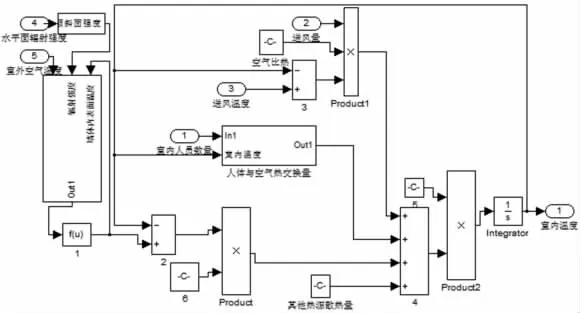
图2 系统仿真模型

3.1 太阳辐射辐射强度对室温的影响

水平面太阳辐射强度由仪器直接测量，强度数值是在上午九时至上午十一时，青岛六月份一晴朗天气条件下测得。图3为室温随太阳辐射强度的变化图。

从图3 中可以看出，当其他条件不变时，总体上随着太阳辐射强度的增加，室温逐渐升高。太阳辐射强度由510W/m2增加至673W/m2，室温由最初的25℃升高至25.31℃，可见太阳辐射强度对室温的影响较小，室温升高在人体可接受的范围。随着太阳辐射强度的增加，室温变化速度先增加后逐渐减小。

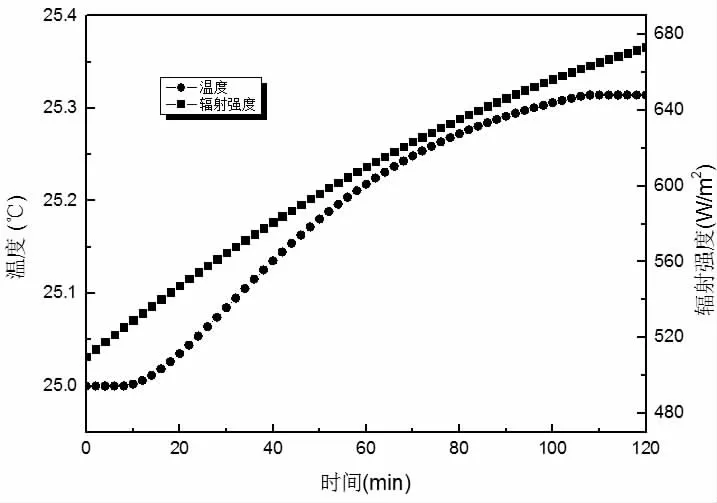
图3 室温随太阳辐射强度的变化图

3.2 室内人员数量对室温的影响

仿真系统运行的初始条件设定空调房无人，当空调房办公区有工作人员（12 人）存在时，室温随时间的变化如图4 所示。

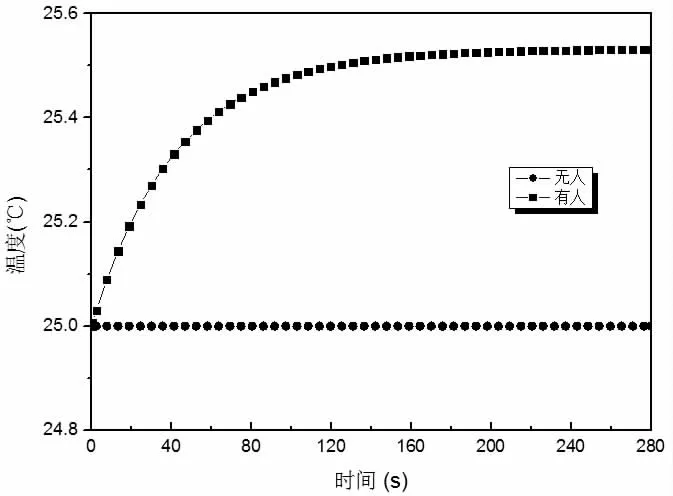
图4 室内人员数量对室温的影响

从图4 可以看出，若其他条件不变，室内无人员流动时，室温会一直保持稳定，当室内人员增加则室温也会逐渐增加直到达到新的稳定值，此时室温为25.53℃，较无人时增加0.53℃，稳定所需的时间大概为260s，这是因为当室内有人员存在时，人体通过呼吸作用、辐射作用以及与空气之间的对流来与空气进行热交换，从而影响温度场。

3.3 送风量对室温的影响

空调系统送风量由风机控制，因而送风量可以实现阶跃变化，当仿真系统送风量分别增大为0.43Kg/s，0.53kg/s 和0.63Kg/s时，空调房室温随时间的变化如图5 所示。

从图5 可以看出，当系统送风量增大时，室温逐渐降低并最终趋于稳定，这是由于送风量的增大导致由风带走的热量随之增大，因此随着时间的推移室温会逐渐降低，系统达到稳定需要的时间约为280s。送风量越大，系统达到的温度稳态值越低，当送风量为0.43Kg/s、0.53Kg/s 和0.63Kg/s 时，稳态值分别为24.6℃，24.0℃和23.6℃。

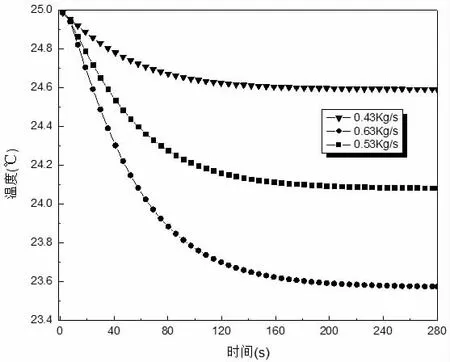
图5 送风量变化对室温的影响

4 结论

依据能量守恒的原则分别对房间空气温度对象和围护结构温度对象建立动态数学模型，同时利用Matlab/Simulink 软件对整个空调房进行了动态模拟，在研究过程中重点探讨了送风量、室内人员数量以及太阳辐射强度对室温的影响，结果表明，这三者均能对房间温度产生一定程度的影响，通过系统模拟，可以更有针对性的对利用空调系统对房间温度进行调控，从而达到节能的目的。