干线动态协调控制的深度Q 网络方法*
2020-06-22郭瑝清
郭瑝清 ,陈 锋 ,2
(1.中国科学技术大学 信息科学技术学院,安徽 合肥230027;2.安徽中科龙安科技股份有限公司,安徽 合肥230088)
0 引言
随着城市人口的增多与经济的快速发展,我国汽车保有量不断增长,城市交通拥堵问题日益严峻。而城市交通干线是城市交通的动脉,实现干线各交叉口间交通信号的动态协调,有效地疏导干线车辆,对于缓解城市交通拥堵具有重要意义。
目前,城市主干道多交叉口的协调控制,主要采用Maxband 和Multiband 法以及图解法、数解法等绿波方法。LITTLE J D C 等人[1]最早提出最大绿波带宽Maxband 模 型;GARTNER N H 等 人[2]在Maxband 模型的基础上,提出复合绿波带宽Multiband 模型;陈昕等人[3]对图解法进行了优化,基于绿波带的中心线交点,设计了一种新的双向绿波图解法;卢凯等人[4]在绿灯中心点型双向绿波协调设计数解法的基础上,建立了一种绿灯终点型的双向绿波数解法,从而减少了干线车队的延误时间;曲大义等人[5]在绿波协调中考虑了公交车辆的影响,并通过增加绿信比与对公交车辆适当的提速,进一步提升了交叉口的通行效率。
现有的绿波方法难以准确地描述复杂的城市干线交通流状态,且采用静态的控制模式,无法有效地协调时变的干线交通流。 随着人工智能的不断发展,采用深度强化学习实现城市交通信号优化控制已成为研究的热点。 HA-LI P 等人[6]为提高交叉口通行能力,提出了一种基于深度强化学习算法的单交叉口信号优化控制方法;GAO J 等人[7]提出一种深度强化学习算法,从实时的交通流数据中自动提取有用特征,实现单交叉口交通流的自适应控制, 并采用经验回放和目标网络技术[8],提高了算法的稳定性;LI C C等人[9]为提高城市路网通行能力,提出了一种用于区域交叉口交通信号控制的深度强化学习算法, 通过多智能体学习最佳的交通信号控制策略;VAN DER POL E[10]采用Max-plus 算法和基于深度强化学习的多智能体方法,实现城市交通区域协调控制。
在深度强化学习领域,目前对于城市交通信号控制的研究,多以单交叉口为研究对象,而对于多交叉口的协调处理,普遍采用多智能体的协调控制。本文结合了双重深度Q 网络(Double Deep Q Network,Double DQN)[11]与基于竞争架构深度Q 网络(Dueling Deep Q Network,Dueling DQN)[12],设计了基于DDDQN(Dueling Double Deep Q Network,DDDQN)的干线动态协调控制算法。 通过将干线多交叉口的交通信号作为一个整体进行处理,相比于采用多智能体协调控制,减轻了智能体间通信协调的负担,且智能体通过获取多交叉口的实时状态,掌握干线全局信息,并使用Dueling DQN 网络结构模型,能更充分地发挥网络提取干线交通流特征的能力,挖掘出多交叉口间协调控制的相关性。 实验结果表明,本文方法相比于现有绿波方法、经典的深度Q 网络(Deep Q Network,DQN)[13]、以及Double DQN 与Dueling DQN,能够更有效地降低城市主干道的车均延误和车辆的停车次数等重要的交通评价指标。
1 DDDQN 介绍
1.1 Q 学习算法
Q 学习算法是由WATKINS C J C H 等人[14]提出的一种无模型强化学习算法。 在Q 学习中,智能体通过与环境交互获得奖励来进行学习,以使得自身能根据当前的状态选择最优的动作。 具体过程描述如下:在与环境交互过程中,t 时刻智能体观测到的状态为st, 当执行了某一动作at后, 环境转移到下一状态st+1,此时智能体会获得一个相应奖励rt。 智能 体 根 据 所 有 记 录 (st,at,rt,st+1), 更 新 状 态 动 作的Q 值,即Q(st,at)。
1.2 DQN 算法
Q 学习通过表格的形式来存储Q 值,而对于城市干线复杂的交通流,其状态空间巨大,表格形式的存储显然无法满足需求。 结合深度学习方法,采用DQN 算法,通过深度神经网络来拟合Q 值函数。
DQN 算法引入经验回放和目标网络两大技术[8]。 智能体在与环境交互中,通过经验缓冲区存储(st,at,rt,st+1)形式的样本,在学习的过程中,再从经验缓冲区中抽取样本,经过深度神经网络的训练学习,调整网络参数,以此达到拟合Q 值函数,实现最优策略的选取。 当t 时刻输入状态st时,输出的目标Q 值为:
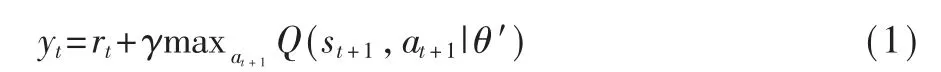
式中γ∈(0,1)表示折扣因子,θ′表示目标网络参数。
1.3 DDDQN 算法
DQN 算法的目标Q 值是通过贪婪法得到的,虽然这样可以让Q 值逼近可能的优化目标,但是容易导致过估计。 为了解决这一问题,Double DQN 算法被提出[11],该算法通过解耦目标Q 值动作的选择与目标Q 值的计算,达到消除过估计问题。 Double DQN的目标Q 值计算如式(2)所示:

而WANG Z Y 等人[12]针对DQN 的网络结构模型进行优化,提出了Dueling DQN。 该算法将深度神经网络分成两部分,一部分表示价值函数,这部分仅仅与状态st有关,与具体采用的at无关;而另外一部分称为优势函数, 同时与状态st和动作at相关。 所以最终的Q 值函数可以表示为:

式中V(st,ω,μ)表示价值函数,A(st,at,ω,β)表示优势函数,ω 为公共部分的网络参数,μ 为价值函数独有部分的网络参数,β 为优势函数独有部分的网络参数。
本文结合Double DQN 与Dueling DQN 算法,对DQN 存在的过估计问题和深度神经网络结构同时优化,并根据干线交通流特性,设计了基于DDDQN的干线动态协调控制算法。 基于DDDQN 算法设计的目标Q 值计算如式(4)所示:

式中,ω、μ、β 为当前网络的网络参数,ω′、μ′、β′为目标网络的网络参数。 DDDQN 算法深度神经网络定义的损失函数如式(5)所示:

网络训练时,还对优势函数部分做了中心化处理,得到如下公式:

式中A 表示优势函数输出的动作空间价值。
2 基于DDDQN 的干线动态协调控制设计
本节将针对城市交通干线的动态协调控制,定义DDDQN 算法的状态空间、动作空间、奖励函数,以及对深度神经网络结构进行设计。
2.1 状态空间
如图1 所示,以经典的三个交叉口组成的城市交通干线为例。 将干线上各交叉口所有入口道车辆的位置信息、速度分布情况以及各交叉口当前相位作为深度神经网络的输入。 考虑第一个交叉口入口道a,距离停车线长度为L 的路段,将每个车道等分为长度为c 的多个小路段,每段记为Cell。 假设车辆占用了长度为c′的Cell 空间,则该Cell 的值为c′/c,所有的Cell 值构成了入口道a 的位置矩阵,而在速度矩阵中,取每个Cell 内所有车辆速度的平均值。干线的位置矩阵和速度矩阵由干线上所有入口道的位置矩阵和速度矩阵组成。
入口道a 的车道划分如图2 所示,对应的位置矩阵、速度矩阵分别如图3、图4 所示。

图1 城市交通干线示意图
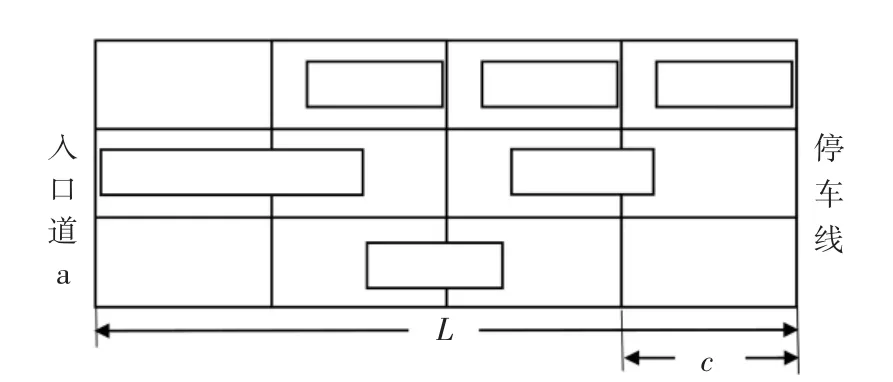
图2 入口道a 车道划分示意图

图3 入口道a 位置矩阵图
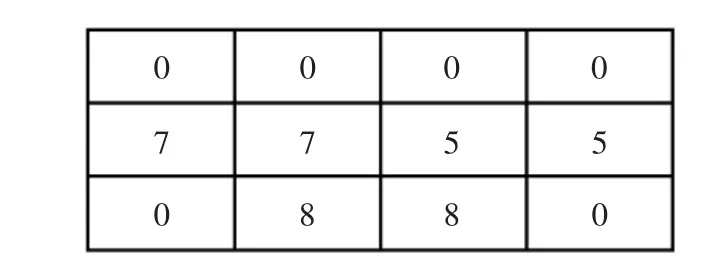
图4 入口道a 速度矩阵图
同时将干线上各个交叉口当前相位形成的相位矩阵作为深度神经网络的输入。 假设干线上3 个交叉口的相位均为典型的4 相位,其相位空间如图5所示,定义相位空间 p={EW,EWL,SN,SNL},分别表示东西直行、东西左转、南北直行、南北左转4 个相位。 且假设当前干线上3 个交叉口的交通信号状态均为东西直行,则相位矩阵表示为[EW,EW,EW],并在输入深度神经网络前,转换为该相位在相位空间的位置序号,EW 在相位空间位于第一个,即相位矩阵为[1,1,1]。

图5 相位空间
2.2 动作空间
智能体根据干线当前的交通状态,选择相应动作对各个交叉口交通信号进行控制,以达到动态协调干线交通流的目的。 本文将干线作为整体进行处理。每个交叉口的动作空间如图6 所示,定义ai={0,1}。当ai=0 时,第i 交叉口保持当前相位1 s;当ai=1 时,切换至下一个相位,相位切换按照相位空间顺序循环切换。 为更适用现实情况,达到更好的控制效果,对待执行动作做如下限制: 当前相位持续保持时间不小于交叉口的最小绿灯时间,才允许切换至下一相位,否则继续保持当前相位;若当前相位持续保持时间大于交叉口的最大绿灯时间,则强制切换至下一相位。 为进一步确保各个交叉口的交通安全性,在相位切换前,通过设置黄灯进行过渡,即当ai=1 时,先执行一个黄灯状态,黄灯保持时间为3 s。
每个交叉口用一位二进制对其动作编码表示,所以对于n 个交叉口的交通干线,需要n 位二进制,动作空间的动作总数为2n。
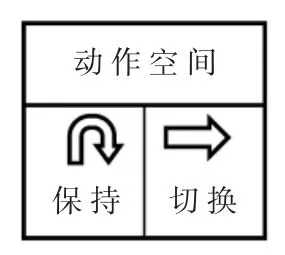
图6 动作空间
2.3 奖励函数
智能体根据获得的奖励来调整所选取的最佳动作,使得长期累积奖励最大。本文定义的奖励为:

式中,Dt表示t 时刻各个支路延误的集合,在所有支路中,当存在某一支路的延误超过给定的阈值D时,给予智能体惩罚;否则考虑主干道是否有延误产生,奖励为主干道延误dt的倒数,即延误越低,奖励越大;当主干道不存在延误,即dt=0 时,给予智能体最大奖励。
2.4 深度神经网络结构
本文设计的深度神经网络结构如图7 所示。 将干线的车辆位置矩阵和速度矩阵以及各交叉口当前相位组成的相位矩阵作为深度神经网络的输入。位置矩阵和速度矩阵经两层卷积层提取相应的特征,并将特征展开为一维,与相位矩阵经过一个全连接层后,两者一起输入全连接层,并将最后一层全连接层分成价值V 和优势A 两部分,并根据式(6)融合两部分输出,最终输出Q 值。

图7 深度神经网络结构
训练时,深度神经网络采用Adam 优化器和ε 贪心策略进行网络输出动作的选取。 ε 值随着训练次数的增加而增加,并最终以0.999 的概率选择深度神经网络输出最大价值的动作。
3 仿真实验及分析
3.1 仿真环境与参数设置
本文的仿真实验平台选择中国科学技术大学微观交通仿真平台2.1(USTC Microscopic Traffic Simulator 2.1,USTC-MTS 2.1)。 算法模型通过Python 实现,并采用PyTorch 搭建深度神经网络结构。
参数设置:折扣因子γ=0.9,经验池大小M=2 000,神经网络学习率为0.001,卷积核大小为5×5,批处理大小为32,训练循环轮数为400,车道划分取c=6 m。 干线上各交叉口间距如表1 所示。

表1 干线各交叉口间距
实际生活中,交通拥堵普遍发生在近饱和交通流量状态下,并且在进行干线协调控制时,主干道上各个交叉口往往已存在车辆排队。 为使实验更贴近现实情况,本文研究在近饱和流量,且主干道形成初始排队情况下的干线协调控制。 主干道各个入口道的平均初始排队长度如表2 所示。

表2 主干道入口道平均初始排队长度
3.2 结果分析
在近饱和流量和主干道存在初始排队的情况下,将本文方法与现有绿波方法(用GW 表示)、经典DQN 算 法、Double DQN 和Dueling DQN 进 行 比 较。指标参数选择干线车均延误和停车次数,实验结果如图8、图9 所示。

图8 车均延误
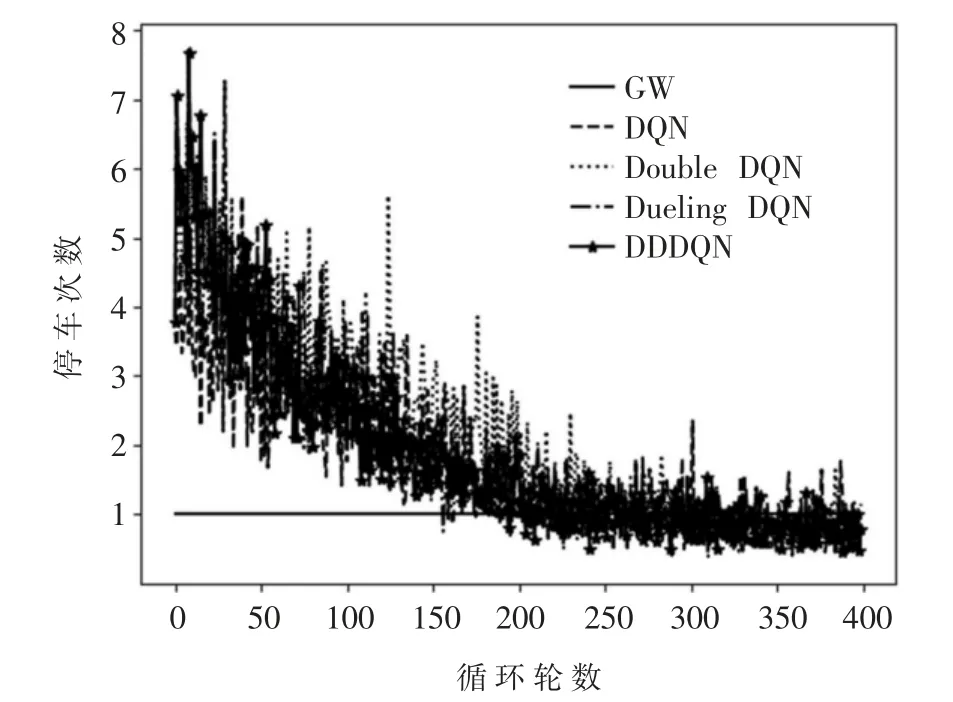
图9 停车次数
根据实验结果,各类算法在主干道平均每轮的车均延误与停车次数如表3 所示。
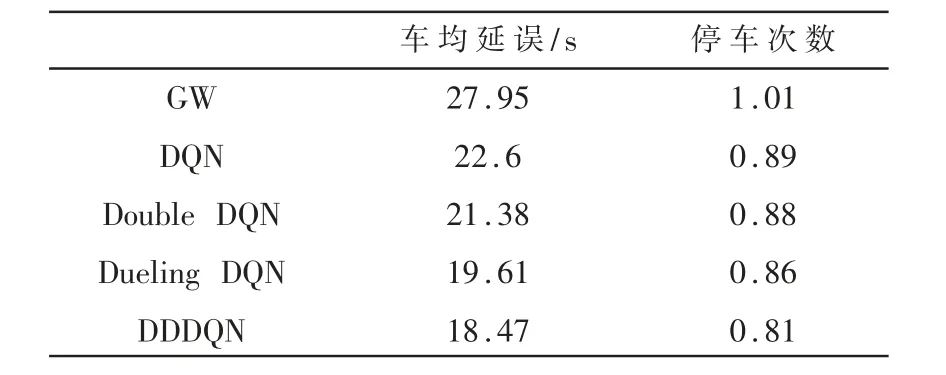
表3 算法性能比较
从表3 可见,采用DQN 算法及其相关改进算法Double DQN、Dueling DQN 以及本文的DDDQN 算法,相比于现有绿波方法,在城市干线的车均延误与车辆停车次数等重要交通评价指标方面均有较大的改善。 说明基于DQN 设计的算法能根据实时的交通流状态,对干线各个交叉口交通信号实现动态协调控制,相比于现有绿波方法,能够更加有效地降低主干道的车均延误与停车次数,进一步改善城市交通拥堵现象。 其中使用基于DDDQN 的干线动态协调控制算法,其干线的车均延误与停车次数均为最小,算法性能最优。 且从图8 的车均延误曲线与图9 的停车次数曲线可以看出,相比于采用经典DQN算法以及单独使用Double DQN 与Dueling DQN,采用DDDQN 算法的车均延误曲线与停车次数曲线波动程度最小,最为稳定,且收敛速度较快,对城市干线的动态协调效果最优。
4 结论
本文将深度强化学习方法引入到城市交通干线的动态协调控制中,结合Double DQN 与Dueling DQN,给出了一种DDDQN 的干线动态协调算法。 通过解耦目标Q 值动作的选取与目标Q 值的计算,消除了DQN 的过估计问题,同时对深度神经网络结构进行优化,将输出分为状态价值与动作优势两部分,并做了中心化处理,使得智能体能更好地进行干线交通信号决策控制。 并且本文将干线作为一个整体处理,通过将干线整体的交通状态输入深度神经网络,能够更充分发挥网络挖掘干线各交叉口协调控制的相关性。 实验结果表明,DDDQN 算法较现有绿波方法、经典的DQN、Double DQN 与Dueling DQN,有效地降低了城市干线的车均延误与停车次数。 后续工作考虑将DDDQN 算法的应用扩展至城市路网,实现区域协调优化控制。
