空射弹道式高超声速导弹多学科优化设计研究

张力聪，朱亮聪，舒忠平，欧岳峰，粟 华

空射弹道式高超声速导弹多学科优化设计研究

张力聪1,2，朱亮聪3，舒忠平3，欧岳峰3，粟 华1,2

（1. 西北工业大学航天学院，西安，710072；2. 陕西省空天飞行器设计重点实验室，西安，710072；3. 上海宇航系统工程研究所，上海，201109）

空射弹道式高超声速导弹是目前最接近实用的高超声速飞行器，为研究该导弹的性能采用多学科优化设计（Multidisciplinary Design Optimization，MDO）技术，对该导弹设计中所涉及的学科进行集成，构建了该导弹的MDO框架，并基于此框架对导弹开展优化设计。优化结果显示了该导弹的潜在性能，同时为该导弹的改进和发展提供了依据。

空射弹道导弹；高超声速飞行器；多学科设计优化

0 引 言

高超声速技术因其较高的战略价值，得到世界各国的广泛关注与不断发展，至今基本形成了助推滑翔式和吸气式两种基本类型的高超声速飞行器[1]。其中，助推滑翔式，由于其技术难度相对较低，已取得了较大的突破。空射弹道式高超声速导弹是助推滑翔式中的一种，其由空中发射平台发射，具有与弹道导弹相同的气动布局与动力系统，已成为最接近实用的高超声速飞行器。最典型代表为俄罗斯的匕首导弹，该导弹已于2017年底进行试验性战斗执勤[2]。

本文针对空射弹道式高超声速导弹开展多学科设计优化研究，以期对该导弹的性能进行分析，进一步挖掘该导弹的潜在性能，并对该导弹的改进和发展提供设计依据。作为高超声速飞行器，该导弹的设计涉及多个学科，且学科间耦合严重。因此，本文采用多学科优化技术对其进行研究，该方法在飞行器设计领域中已被广泛应用[3,4]，其能有效解决学科间的耦合关系，并对其进行综合设计，获得总体性能更优的设计结果。

本文首先建立了空射弹道式高超声速导弹的多学科设计优化框架，然后对所涉及的几何、气动、发动机、布局、弹道、结构及战斗部学科的分析模型进行阐述。基于该框架，对导弹开展多学科设计优化，并对结果进行分析，得到了该导弹的潜在性能及设计依据。

1 空射弹道式高超声速导弹MDO框架

空射弹道式高超声速导弹的设计主要涉及几何、气动、发动机、布局、弹道、结构和战斗部7个学科。要构建多学科优化设计（Multidisciplinary Design Optimization，MDO）框架，首先要对参数进行梳理，框架中存在3种类型的变量：设计变量、耦合变量与状态变量。设计变量是各个学科的独立输入，同时在优化中作为设计变量；耦合变量为学科之间的传递参数，既是一个学科的输出又是另一个学科的输入；状态变量是各个学科的独立输出，在优化中可被选作约束条件或目标函数。然后，根据数据传递关系可将各个学科集成并建立该导弹的MDO框架，如图1所示。

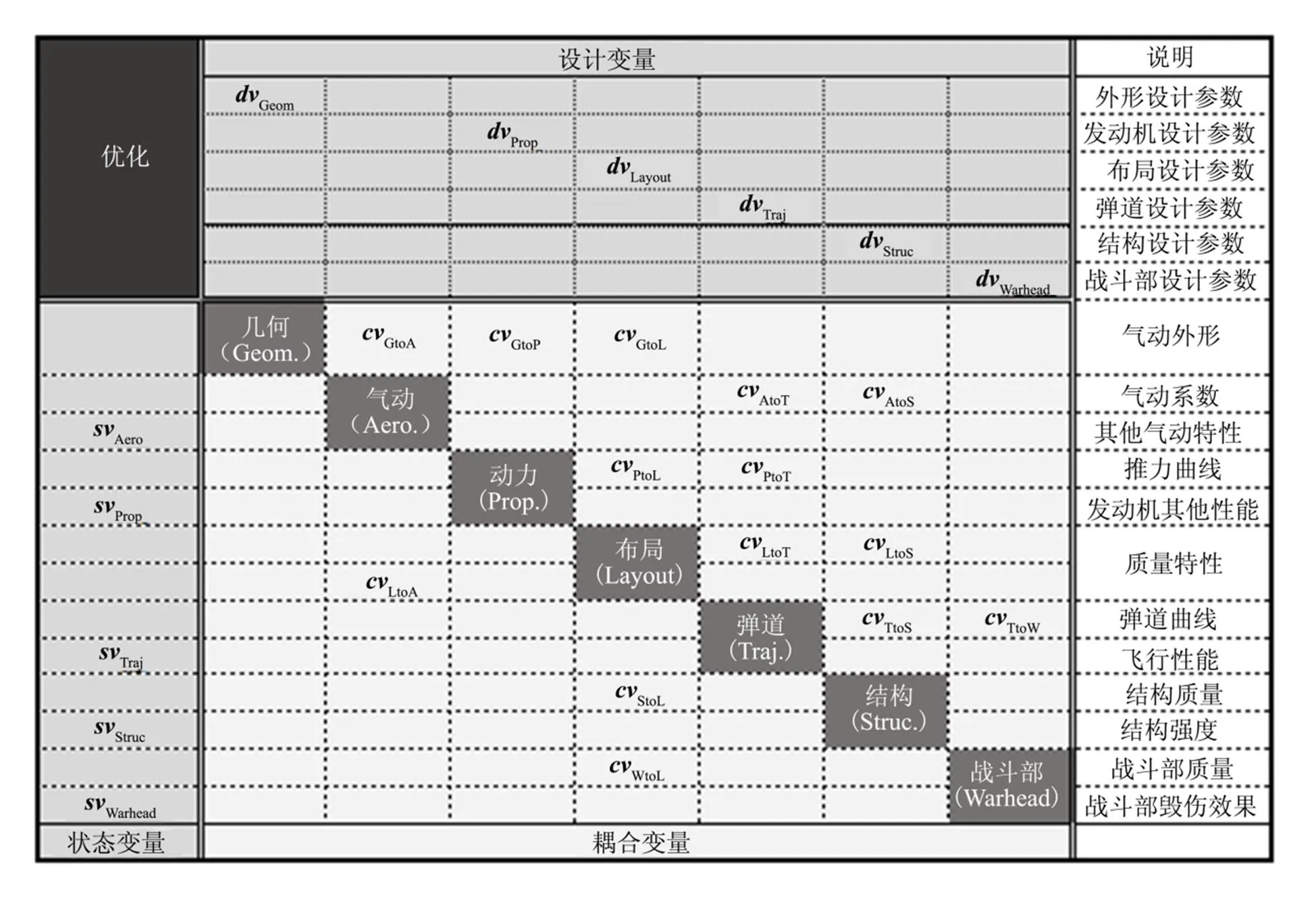
图1 设计结构矩阵

2 多学科分析模型

2.1 几何及气动分析模型

几何学科对导弹的气动外形进行参数化设计，如图2所示，该导弹采用无翼式布局，因此，气动外形设计集中在弹体和舵面的设计上。然后，气动学科采用高速面元法对该外形的气动特性进行分析，该方法对高超声速飞行器的气动特性计算具有一定的精度[5]，同时能够在优化迭代时，保证较高的计算效率。气动分析一方面为弹道学科输出升力系数L和阻力系数D，同时为结构分析学科输出气动压力分布()，并且计算出导弹配平攻角b以衡量导弹的操稳特性。该学科的输入输出关系如表1所示。

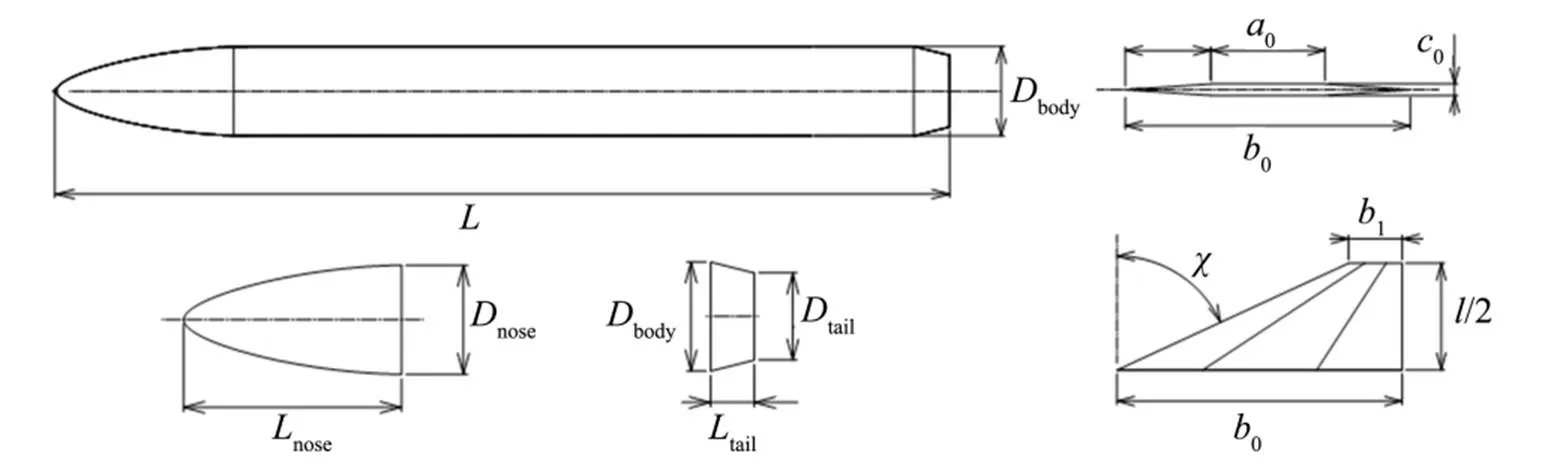
图2 气动外形参数化

—弹体总长；body—弹体直径；nose—头锥长度；nose—头锥直径；tail—尾部长度；tail—尾部直径；0—舵面根弦最大厚度长度；0—舵面根弦长；0—舵面根弦最大厚度；1—舵面梢弦长；—舵面前缘后掠角；/2—舵面半展长

表1 几何及气动学科输入输出

Tab.1 Inputs and Outputs of Geometry-and-aerodynamic Discipline

输入变量类型dvGeom 变量LnoseLbodyDbodyDtail 说明头锥长度弹体长度弹体直径尾部直径 变量类型—cvLtoG—— 变量b0xcg—— 说明舵面根弦长质心—— 输出变量类型cvAtoTcvAtoSsvAero 变量CL(Ma,α)CD(Ma,α)p(x)δb 说明升力系数阻力系数压力分布配平攻角

2.2 发动机分析模型

该导弹的动力系统与常规导弹相同，采用固体火箭发动机，如图3所示。

在发动机分析学科中，首先对发动机的燃烧室、喷管和药柱进行设计。然后采用零维内弹道方程对固体火箭的性能进行评估，导弹的燃烧室压强c()可由式（1）计算得到：

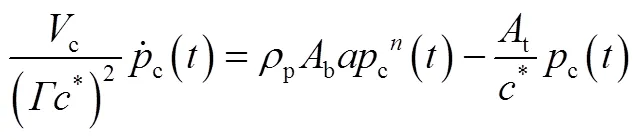
式中 Vc为燃烧室的自由容积；Ab和At分别为燃面面积和喷管喉部面积；ρp为固体装药的密度；Γ，c*和a均为与推进剂燃烧相关的特征常量；n为压强指数，是推进剂的特征常量。然后，基于此一方面为弹道分析学科输出推力T(t)和发动机秒流量ms，同时，为布局分析学科输出发动机总质量mmotor。并且，计算发动机的比冲和总冲以评估发动机性能。最终，该学科的输入输出关系如表2所示。

ch—燃烧室直径；ch—燃烧室长度；propellent—药柱长度；—药柱肉厚；throat—喉部长度；throat—喉部直径；exit—出口直径；nozzle—喷管扩张角

表2 发动机学科输入输出

Tab.2 Inputs and Outputs of Propulsion Discipline

输入变量类型dvProp 变量LchDthroatDexite 说明燃烧室长度喉部直径出口直径装药肉厚 变量类型dvPropcvGtoP—— 变量LpropellantGeoshape—— 说明装药长度外形约束—— 输出 变量类型cvPtoTcvPtoL 变量F(t)msmmotor 说明推力秒流量发动机总质量 变量类型svProp— 变量pcIIs— 说明燃烧室压强总冲比冲—

2.3 布局分析模型

布局分析学科对导弹的内部布局进行设计，并对该布局的质量特性进行计算，包括质心cg，用于计算导弹的气动操纵性能；总质量total将作为弹道仿真的输入；同时还包括质量分布()将用于结构分析。最终，该学科的输入输出关系如表3所示。

表3 布局学科输入输出

Tab.3 Inputs and Outputs of Layout Discipline

输入变量类型dvLayout.cvGtoL 变量xcgdevicesmdevicesGeodevicesGeoshape 说明设备位置设备质量设备外形气动外形 变量类型cvPtoLcvStoL 变量Geomotormmotormequ.struc.(x) 说明发动机外形发动机质量结构质量 输出变量类型cvLtoScvLtoAcvLtoT— 变量m (x)xcgmtotal— 说明质量分布质心总质量—

2.4 弹道分析模型

弹道分析学科，对导弹的弹道进行仿真计算，而后分析其飞行性能，包括过载、马赫数和射程等。此时，关心导弹的质心运动，因此，常采用铅锤平面质心运动方程式（2）对导弹的飞行性能进行仿真分析。

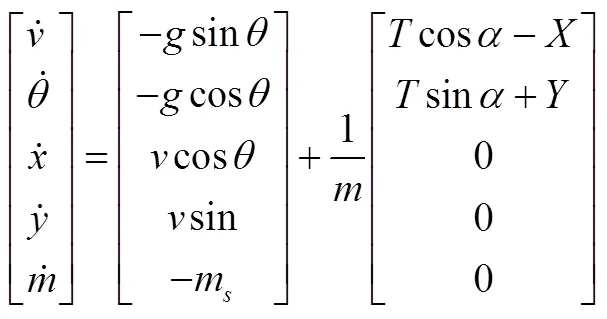
式中 (,,,,)T为导弹的飞行状态，分别为速度、弹道倾角、水平位置、垂直高度和质量；为重力加速度；为导弹飞行攻角；为发动机的推力；，为导弹所受的气动阻力和升力。该学科的输入输出关系见表4。

表4 弹道学科输入输出

Tab.4 Inputs and Outputs of Trajectory Discipline

输入变量类型dvTrajcvAtoTcvPtoT 变量αcontrolCL(Ma,α)CD(Ma,α)F(t) 说明控制规律升力系数阻力系数推力曲线 变量类型—cvLtoT—— 变量msmtotal—— 说明秒流量总质量—— 输出 变量类型cvTtoScvTtoWsvTraj 变量nmaxvendθendR 说明最大过载点末速度落角射程 变量类型———— 变量Mamax——— 说明最大马赫数———

2.5 结构分析模型

结构分析学科根据弹道仿真所得出的最大过载点及气动分析计算得到的气动压力分布，使用梁模型对导弹所受载荷进行计算，包括轴力、剪力和弯矩。然后根据所受载荷对导弹的结构质量进行评估，如图4所示。因此，该学科的输入输出关系如表3所示。

图4 结构分析示例

表5 结构学科输入输出

Tab.5 Inputs and Outputs of Structure Discipline

输入变量类型cvTtoScvAtoScvLtoS— 变量nmaxp(x)m (x)— 说明最大过载压力分布质量分布— 输出变量类型cvStoLsvStruc. 变量mequ.struc.(x)N(x)Q(x)M(x) 说明结构质量轴力分布剪力分布弯矩分布

2.6 战斗部毁伤分析模型

战斗部毁伤分析学科，对该导弹所使用的破片战斗部，采用射击迹线法[6]，对其对典型雷达目标[7]的毁伤效果进行分析，如图5所示，可得到破片在空间中的分布及飞行速度。然后，可对命中破片数进行统计，并对杀伤动能hit进行计算，以评估战斗部的毁伤效果，从而对战斗部质量warhead进行合理设计。该学科输入输出关系如表6所示。

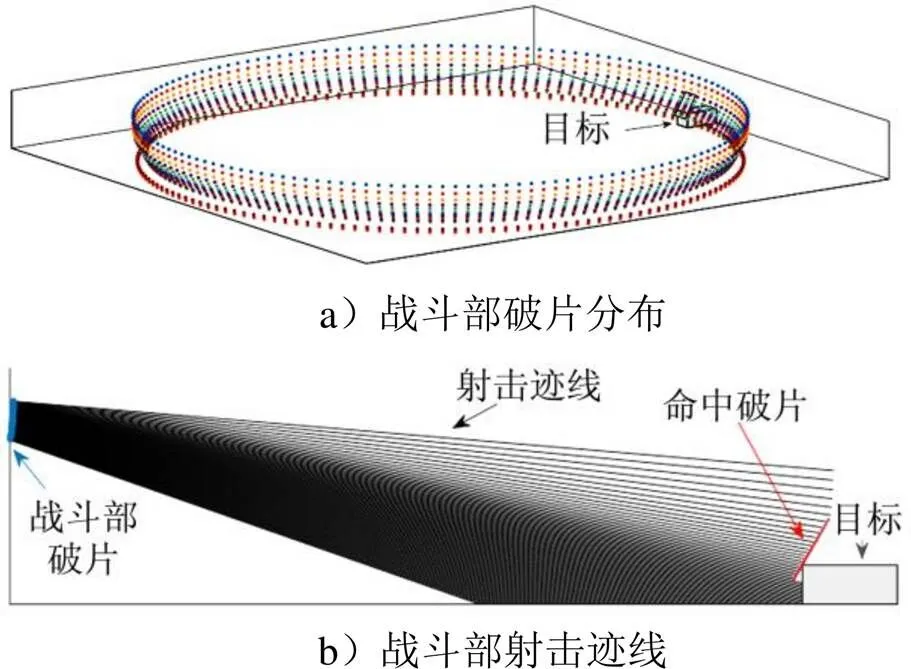
图5 战斗部分析示例

表6 战斗部学科输入输出

Tab.6 Inputs and Outputs of Warhead Discipline

输入变量类型dvWarhead 变量LwarheadDwarheadmfragrments 说明战斗部长度战斗部直径破片质量 变量类型—cvTtoW— 变量mexplosivesvendθend— 说明装药质量末速度导弹落角— 输出变量类型cvWtoLsvWarhead—— 变量mwarheadJhit—— 说明战斗部质量杀伤动能——

3 优化问题

3.1 目标函数

在导弹优化设计中，有许多可选的目标函数，如射程、飞行速度和发射质量等。其中，减小发射质量是所有飞行器在设计时的首要目标，同时，质量特性也是与导弹设计所有学科耦合最为严重的指标，它既由许多学科的输出决定，又是很多学科的输入，如图6所示。因此，在工程中通常将最小化发射质量作为导弹优化设计的目标函数。

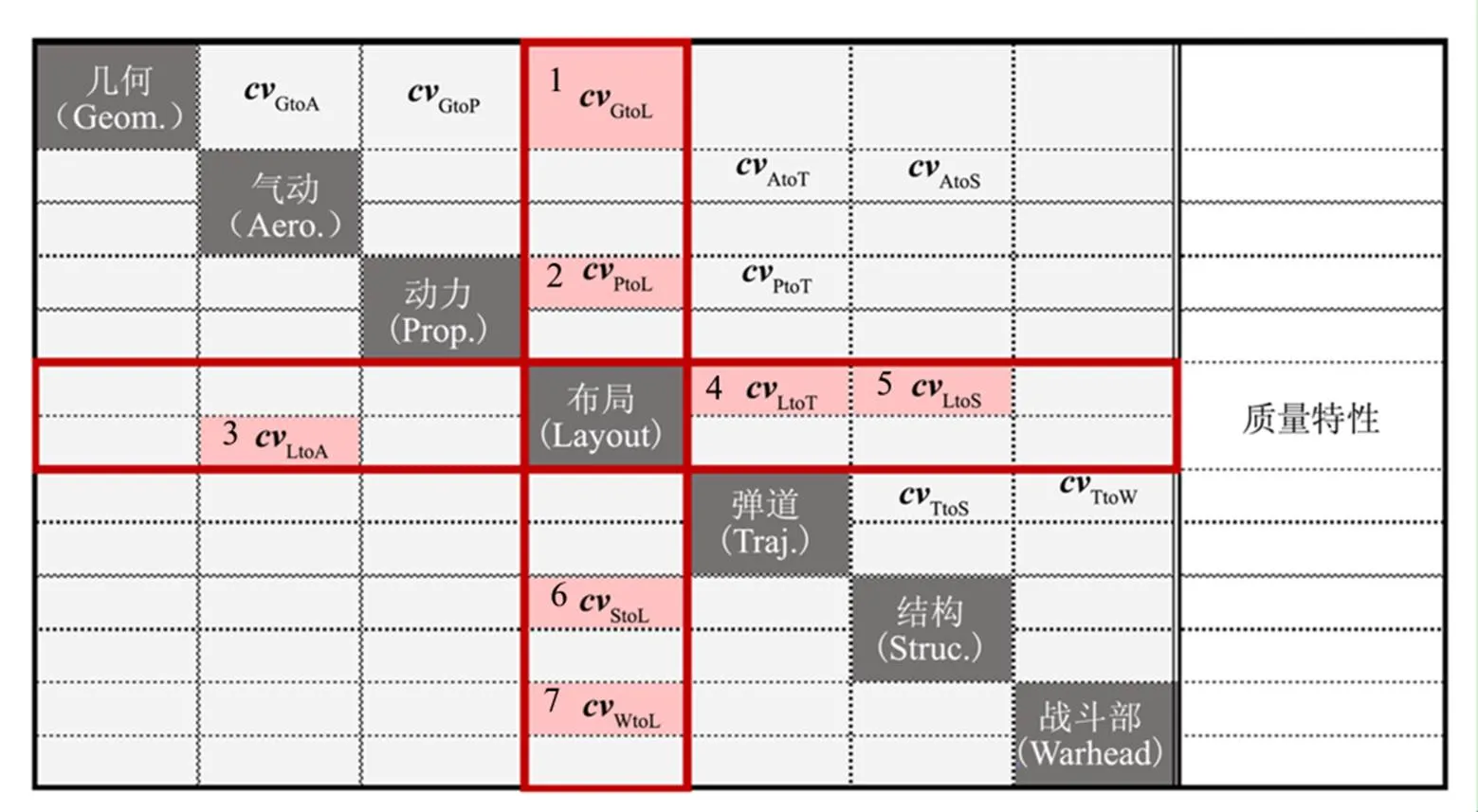
图6 导弹质量特性的耦合关系

3.2 设计变量

根据各个分析学科的输入输出关系，该导弹的优化设计问题，在几何学科、发动机学科、布局学科、弹道学科及战斗部学科中存在14个设计变量，如表7所示。

表7 设计变量

Tab.7 Design Variables

设计变量说明设计变量说明 dvGeom.Lnose头锥长度dvPropLc燃烧室长度 Lbody弹体长度Dthroat喉部直径 Dbody弹体直径dvTrajαcontrol控制规律 Dtail尾部直径dvWarheadLwarhead战斗部长度 b0舵根弦长Dwarhead战斗部直径 dvLayoutxcgdevices设备位置mfragrments破片质量 mdevices设备质量mexplosives装药质量

3.3 约束条件

在气动分析学科中，对导弹的升力和阻力特性不做直接约束，其将在导弹的飞行性能中体现，并在弹道分析学科中间接约束。但是，对于导弹舵面的性能需进行约束，以使优化结果具有足够的舵效。因此，本文通过对导弹的配平攻角b进行约束，使优化结果具有足够的机动性和稳定性。

在发动机分析学科中，发动机应具有足够大的比冲s，以使发动机具有较高的性能。同时，发动机燃烧室需有足够的压强以保证燃料能够正常燃烧，而过大压强将造成过高的结构质量，因此，燃烧室压强c应在一个合理范围内。

在弹道分析学科中，为使导弹的飞行性能满足设计指标，需对导弹的射程、速度和落角等飞行性能进行约束。本文中的导弹对马赫数具有较高的要求，因此对最大马赫数max进行约束。而射程在不同的优化问题中将被分别作为约束条件和目标函数。对于落角，通常是为了保证足够的毁伤效果，而本文引入了战斗部分析模型，因此，落角不再做直接的约束。

最后，在战斗部分析模块中，对战斗部的对目标杀伤性能hit进行约束，使导弹能够对目标进行有效的毁伤。综上，本文共建立6个约束条件，如表8所示。

表8 约束条件

Tab.8 Constraints

约束条件公式约束条件公式 gAero.δbL ≤ δb ≤ δbUgTrajR ≥ RL gProp.Is ≥ IsLMamax ≥ MamaxL pcL ≤ pc ≤ pcUgWarheadJhit ≥ JhitL

注：上标L和U分别代表约束条件的下界和上界

3.4 优化模型

与传统导弹优化问题相同，将最小化发射质量作为目标函数，建立单目标优化问题式（3）。该问题使用遗传算法（Genetic Algorithm，GA）进行求解。

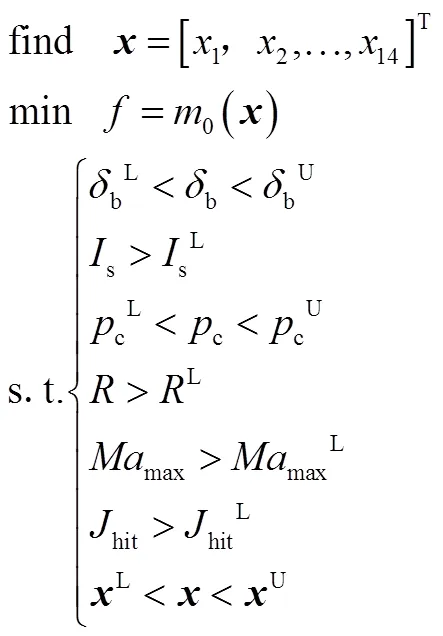
4 优化结果

单目标优化问题的目标函数迭代历程如图7所示。最优解的约束条件与目标函数与基准值的对比如表9所示。其中，目标函数（导弹的发射质量）下降了20.01%。

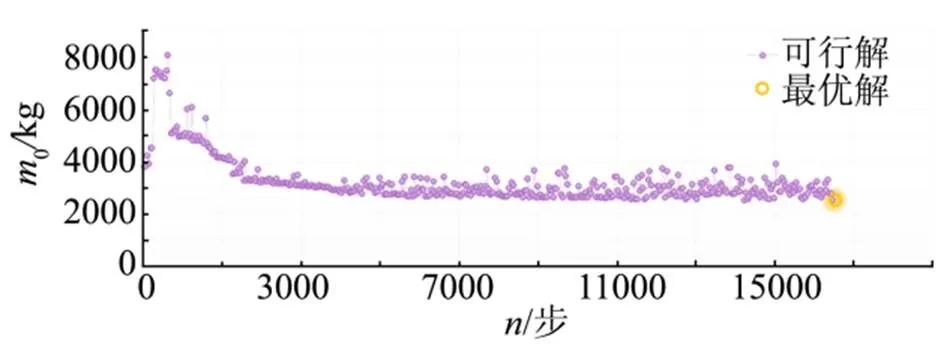
图7 目标优化迭代历程（仅可行解）

表9 约束条件及目标函数优化结果

Tab.9 Optimization Results of the Constraints and Objective

类型变量基准值优化结果约束/增量 约束δb/(°)-17.67-15.16[-25,-10] Is/（Ns·kg-1）2414.262414.27≥2400 Mamax10.8610.33≥10 Jhit/J3039.753009.28≥3000 pc/MPa12.9417.46[15,30] R/km2067.242011.01≥2000 目标m0/kg3263.562545.35-20.01%

设计变量的优化结果如表10所示，同时，导弹的外形与发动机的优化结果如图8所示。可以看到导弹的气动外形尺寸相对于基准方法在长度方向上产生了较大的减小而在直径方向减小较少，该外形能够有效减小导弹的结构质量。同时，发动机的规模也被减小，装药量随即减少，虽然这将降低发动机的总冲，但是由于总质量的下降，发动机依然能够提供足够速度增量，以保证飞行性能不被损失。

表10 设计变量优化结果

Tab.10 Optimization Results of the Design Variables

设计变量基准值优化结果相对值 Lnose/mm3064.052330.95-23.93% Lbody/mm4234.343882.17-8.23% Dtail/mm250.35191.14-23.65% Dbody/mm1027.86998.46-2.86% b0/mm750.16512.72-31.65% Lch/mm2055.351615.68-21.39% Dthroat/mm162.76134.76-17.20% Lwarhead2405.362435.401.25%

图8 导弹外形对比

优化后，虽然导弹尺寸和质量有所减小，但各项性能依然满足设计指标。首先，导弹的射程，由于发动机规模的减小，相对于基准方案有所减小，但依然满足大于2000 km的指标要求，如图9所示。同时，其它飞行性能，如最大马赫数也满足要求。

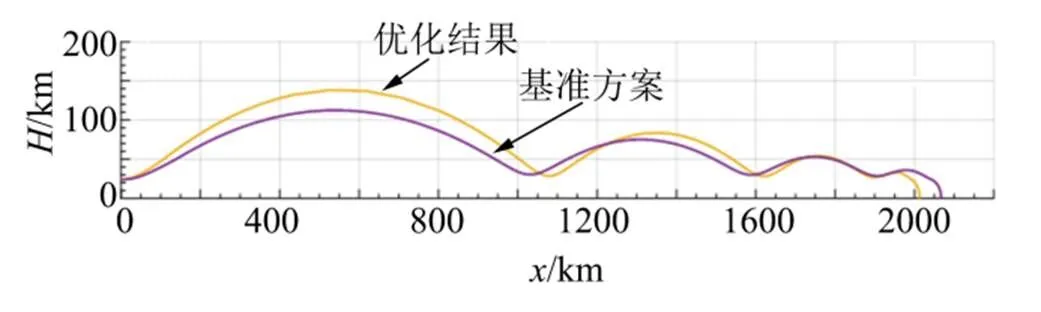
图9 弹道对比

最后，战斗部的毁伤效果是导弹最重要的指标，优化后，导弹的战斗部规模有所增加，杀伤动能满足有效毁伤目标的动能要求。并且，具有更好的起爆条件，如图10所示。

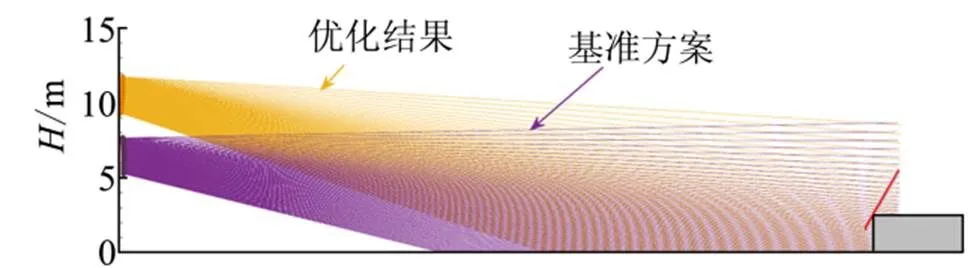
图10 射击迹线对比

5 结 论

本文针对空射弹道式高超声速导弹，建立了其多学科设计优化框架，对学科间的参数耦合关系进行了梳理和阐述，并对该导弹开展了优化设计研究，得到如下结论：

a）本文建立的MDO框架包含几何、气动、发动机、布局、弹道、结构及战斗部学科，学科间参数传递由设计变量、耦合变量和状态变量组成。

b）最小化发射质量的单目标优化问题在满足飞行性能，包括射程、最大马赫数和毁伤效果的前提下，发射质量降低了20.01%

c）引入战斗部毁伤分析模块能够有效地使优化后的导弹具有足够的毁伤能力，并使导弹的终端飞行状态具有更好的起爆条件。

[1] 王少平, 等. 助推滑翔高超声速导弹发展趋势及作战使用研究[J]. 战术导弹技术, 2020(1): 9-14.

Wang Shaoping, et al. Research on development and operational applicationof boost-glide hypersonic missile[J]. Tactical Missile Technology, 2020(1): 9-14.

[2] 林旭斌，张灿. 俄罗斯新型高超声速打击武器研究[J]. 战术导弹技术, 2019(1): 19-24.

Lin Xubin, Zhang Can. Research on new Russian hypersonic strike weapon[J]. Tactical Missile Technology, 2019(1): 19-24.

[3] 郑安波, 马汉东, 罗小云. 战术导弹多目标多学科设计优化[J]. 航空学报, 2013, 34(11): 2557-2564.

Zheng Anbo, Ma Handong, Luo Xiaoyun. Multiobjective multidisciplinary design optimization of missile[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(11): 2557-2564.

[4] Zandavi S M, Pourtakdoust S H. Multidisciplinary design of a guided flying vehicle using simplex nondominated sorting genetic algorithm II[J]. Structural and Multidisciplinary Optimization, 2018, 57(2): 705-720.

[5] 江志国, 车竞. 基于网格面元法的高超声速飞行器性能分析[J]. 计算机仿真, 2011, 28(3): 56-59.

Jiang Zhiguo, Che Jing. Performance analysisof hypersonic vehicle base on surface element modeling[J]. Computer Simulation, 2011, 28(3): 56-59.

[6] 蒋建伟, 卢永刚, 钱立新. 射击迹线技术在战斗部破片场仿真中的应用[J]. 弹箭与制导学报, 2001(1): 29-34.

Jiang Jianwei, Lu Yonggang, Qian Lixin. Application of shot-line model in simulation of fragment warhead[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2001(1): 29-34.

[7] 李超, 等. 破片式战斗部对典型相控阵雷达毁伤评估[J]. 弹道学报, 2015, 27(1): 80-84.

Li Chao, et al. Assesment of fragmentation warhead damagagin typical phase array radar[J]. Journal of Ballistics, 2015, 27(1): 80-84.

Study on Multidisciplinary Design Optimization ofAero-ballistichypersonic Missile

Zhang Li-cong1,2, Zhu Liang-cong3, Shu Zhong-ping3, Ou Yue-feng3, Su Hua1,2

(1. School of Astronautics, Northwestern Polytechnical University, Xi'an, 710072; 2. Shanxi Aerospace Flight Vehicle Design Key Laboratory, Xi'an, 710072;3. Aerospace System Engineering Shanghai, Shanghai, 201109)

Aero-ballisticmissileis the most likelyhypersonic vehicle to be used incombat, therefore, performance of the missile is investigated based on multidisciplinary design optimization (MDO) technology. Firstly, the disciplines of the missile design are integrated to establish the MDO framework. Then, on this basis,the optimization of the missile is carried out. Finally, the results show the potential performance of the missile and providedesign knowledge for the improvement and development of this type of missile.

aero-ballisticmissile; hypersonic vehicle; multidisciplinary design optimization

1004-7182(2020)03-0008-07

10.7654/j.issn.1004-7182.20200302

V421.1

A

张力聪（1995-），男，博士研究生，主要研究方向为多学科优化设计。

朱亮聪（1983-），男，高级工程师，主要研究方向为运载火箭总体设计。

舒忠平（1980-），男，工程师，主要研究方向为运载火箭载荷设计。

欧岳峰（1983-），男，高级工程师，主要研究方向为飞行器总体设计。

粟 华（1985-），男，博士，副研究员，主要研究方向为导弹总体设计。

2020-05-11；

2020-05-15