“同心协力”团队协作策略探究

纪逸轩

【摘 要】本论文主要研究“同心协力”的团队协作策略。基于对于人的理想化假设，不考虑到人的具体变化，将人只作为力的载体，在假设成立的基础上逐个分析问题。对于问题1部分，基于基本的物理定律：1.运动学定律;2.动量守恒定律，寻找最优的碰撞条件。最终得到要求高度下，各位成员的施力关于时间的变化关系对于问题2部分，先借助均质圆柱类刚体对任意轴的转动惯量计算方法，再通过对运动进行分解，分别获得鼓面相对xoz，yoz平面的倾角变化，结合数学上求二面角的方法，构造单位向量，获得鼓面倾角的变化值，建立了理想状态下的精确协作模型与贴近实际的动力学综合调节模型。问题3引入了现实情形，各名队员在拉鼓绳时难免会产生牵拉的时机、力度不同的情况，产生相对误差，导致球的运动轨迹发生改变，使球跳出鼓面或未能达到指定高度，项目停止。问题3在问题1模型的基础上根据实际情况改进了问题1的颠球模型，保证在球不飞出鼓面的前提下颠球高度始终大于40cm。问题4在限定条件下，综合利用模型1和模型2，通过模型1获分析绳对鼓提供位移的合力和作用时间，在调整球的偏转角度时，利用问题2的已有结论，反解出xoz与yoz平面的转动分量，由此获得xoz和yoz平面上的合力矩，从而确定团队的协作策略。

【关键词】“同心协力”策略;精准协作模型;动力学综合调节模型

一、引言

“同心协力”项目初始状态是有一面牛皮双面鼓，鼓身中间固定多根绳子，绳子在鼓身上的固定点沿圆周呈均匀分布，每根绳子长度相同。团队成员每人牵拉一根绳子，使鼓面保持水平。项目开始时，球从鼓面中心上方竖直落下，队员同心协力将球颠起，使其有节奏地在鼓面上跳动。颠球过程中，队员只能抓握绳子的末端，不能接触鼓或绳子的其他位置。此条件表明，在本问题中人只提供力去影响系统，不产生其他的附加效应。

项目基本限制1.排球的质量为270 g;2.鼓面直径为40 cm;3.鼓身高度为22 cm;4.鼓的质量为3.6 kg;5.队员人数不少于8人;6.队员之间的最小距离不得小于60 cm。球初始落点距鼓面中心上方40 cm，球被颠起的高度应离开鼓面40 cm以上，如果低于40cm，则项目停止。项目的目标是使得连续颠球的次数尽可能多。

基于以上背景本文需要解决的问题为以下几点：

1.设定在每个人都可以精确控制用力方向、时机和力度的理想状态下，根据理想条件设计合适的方案以讨论团队的最佳协作策略。

2.中改变第一问中的条件，并给出了所研究的系统的队员人数、绳长、与鼓面初始位置的具体值，使之变成更加符合实际且复杂的非理想情况。由题意，在非理想状况下，队员发力力度、方向与时机均无法精准掌握，使得鼓面不同时刻产生不同倾角，导致球的颠起方向偏离竖直方向，能够达到的最大竖直方向的高度降低。

3.对第一问中的策略和第二问中的模型进行回顾，通过现实背景，显出了原有的模型的漏洞，引导模型的改进方向。

4.引入第二问的实际情况，即当鼓面发生倾斜时，球跳动方向不再竖直。同时，引入第一问中的所有队员都能精准控制发力时机和力度的条件。因此，调整拉绳策略，即是给出在可精确控制条件下所有队员的发力时机及力度的同时，能够在现实情形中检验这种调整策略所对应的数学模型，并分析调整后的拉绳策略的实用性。

二、模型假设

1.假设牛皮双面鼓为一个质地均匀的刚性圆柱体，鼓的平动只沿竖直方向。

2.假设团隊成员之间距离相等，到鼓中心的距离也相等，且在拉动绳子的过程中各成员位置保持不变。

3.假设在拉动过程中每根绳子与水平面的夹角相同，忽略由于鼓面倾斜造成绳子与水平面的夹角的变化。

三、模型的建立与求解

3.1问题一

3.1.1建立模型

根据已知条件，“同心协力”协作项目的目标是使得连续颠球的次数尽可能多。最终颠球次数取决于球飞行的角度和高度，如果球偏离竖直方向的角度过大，则会导致球飞出鼓面正上方的范围，如果球被颠起的高度低于40cm则项目终止。

在理想状态下，每个人都可以精确控制用力方向、时机和力度，故团队成员可同时以相同大小的力拉绳，这样既可以使团队成员平均分摊比赛时消耗的体力，又可以使拉力在水平方向上的分力相互抵消，使鼓面保持水平状态，从而使球保持竖直方向的运动，保证球不飞离鼓面正上方的范围。

球从初始位置下落的过程中，所有队员应当控制鼓先向下运动再向上做加速运动且刚好在球下落40cm时球与鼓发生碰撞。在碰撞瞬间，保持所有绳的拉力在竖直方向上的合力F等于鼓的重力，此瞬间系统合外力为0，动量守恒，当碰撞后球的速度与碰撞前的速度等大反向时，球在碰撞后上升的最大高度刚好为40cm。碰撞后，球开始上升，在球上升阶段，保持所有绳的拉力的合力F等于鼓的重力，使鼓保持静止状态，直到球达到最高点，此时球和鼓又都回到初始状态，如此循环往复，可使项目一直进行下去。

3.1.2模型求解过程

设每名队员拉绳的拉力 是一个周期为2t的周期函数，则在一个周期内的函数满足

其中F为所有绳拉力在竖直方向上的合力， 为绳与竖直方向的夹角。

F的分段函数时间的关系， 为绳拉力为0的时间， 为绳拉力为的时间。

球下落40cm的时间，球下落40cm时的速度，令碰撞瞬间所有绳拉力的合力F等于鼓的重力，碰撞瞬间系统合外力为0，由动量守恒定理[1]，由于碰撞后球的速度与碰撞前的速度等大反向，即于要使绳的合力所 做的功最小，就要使系统在循环过程中鼓所浪费的能量尽可能少，即碰撞后鼓的速度，鼓的速度与时间的关系，鼓的位移与时间的关系，由受力分析可知

联立上述各式可得以下方程组：

3.2问题二

3.2.1建立模型

在现实情形中，队员在拉鼓绳时难免会出现拉绳的时机不同步、力度不相同的情况，于是鼓面可能出现倾斜。本题模型只关心鼓面的转动情况，不考虑鼓的平动情况。在研究鼓的转动时，把鼓视为一个质地均匀的圆柱体刚体，所以鼓面的角度变化可以转化为圆柱体绕质心转动的问题。

3.2.2模型求解过程

以鼓的中心为原点，以鼓的旋转对称轴为z轴，建立空间直角坐标系。鼓绕中心的转动可以分解为鼓面以x轴为轴的转动与以y轴为轴的转动的和转动。

由力矩通过力距的矢量分解可得以x轴为轴转动的力矩以y轴为轴转动的力矩，两者的表达式分别为：

代入数据计算鼓以x轴或y轴为轴转动的转动惯量J=0.05052

代入式可求出鼓面以x轴为轴的转动角与以y轴为轴的转动的转动角为了得到鼓面与xoy平面的夹角，考虑通过求二面角的方法解决问题，而前式得到的仅有两个方向的偏角，为了获得夹角，分别取xoz平面和yoz平面关于沿先前得到的两个转动方向的单位向量，通过两个向量叉乘，得到旋转后鼓面的法向量，取沿z轴的一个单位向量，通过数学上求二面角的方法得到两平面的偏角，即为鼓面0.1s时的倾斜角。通过matlab编程，计算得到鼓面的倾斜角度。[3]计算结果如下表：

3.3问题三

3.3.1建立模型

在现实情形中，根据问题2的结果，问题1中的策略是需要经行调整的。

在现实情形中，队员发力力度与发力时机均无法精准掌握，使得鼓面无法一直保持水平，会在不同时刻产生不同倾角，导致球的颠起方向偏离竖直方向，实际运动路径将为一条抛物线，球被颠起的高度很可能会低于40cm，导致项目停止。本模型对问题1中模型进行改进，进一步考虑实际问题中由于鼓面倾斜导致球颠起高度发生的改变。

3.3.2模型求解过程

由于实际颠球时球的轨迹可以近似为一条抛物线，所以当球的水平位移超过鼓的直径40cm时，球将落在鼓面外。当球的水平位移大于或等于鼓的直径40cm时，速度在竖直方向的分量 ，球飞行到最高点的时间速度沿水平方向的分量合速度所以最小颠球高度 将 代入问题1方程组中解得合力，作用时间 故改进后每名队员拉绳的拉力的函数为

其中l为绳的长度，n为团队人数。

3.4问题四

3.4.1建立模型

任何刚体的一般运动都可以分解成质心的平动和绕质心的转动。本题应当结合问题1与问题2中的模型，综合考虑运动过程中鼓的位移与鼓面的方向。

3.4.2模型求解过程

鼓的位移：将h=0.6m代入问题1中的方程组，解方程组得到绳对鼓提供位移的合力大，作用时间 每名队员距离鼓旋转轴的最短距离 绳与竖直方向的夹角 则每名队员对绳的拉力，拉力沿绳方向。

鼓面转动：

以鼓的中心为原点，以鼓的旋转对称轴为z轴，建立空间直角坐标系。对10名队员按逆时针方向进行编号，队员编号依次为0-9，设编号为0的队员站在x轴上。由于球的反弹高度为60cm，相对于竖直方向产生1度的倾斜角度，设倾斜方向在水平面的投影指向编号为0和1的队员之间，与这两位队员的夹角之比为1：2。球的速度在竖直方向的分量球飞行到最高点的时间，球的速度沿水平方向的分量合速度与竖直方向的夹角，

满足解得球的合速度与竖直方向的夹角

要将球调整为竖直状态弹跳，则鼓面水平方向夹角应为0.25度，则鼓面的法向量可表示为

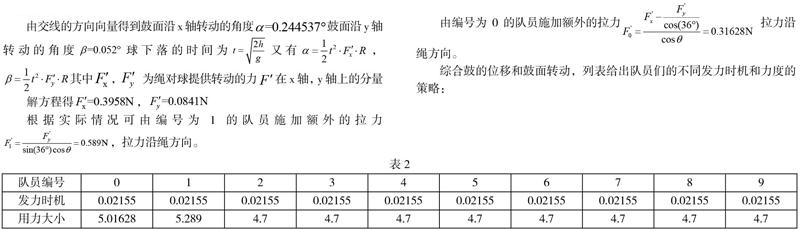
由交线的方向向量得到鼓面沿x轴转动的角度鼓面沿y轴转动的角度球下落的时间为又有，其中， 为绳对球提供转动的力在x轴，y轴上的分量

解方程得，

根据实际情况可由编号为1的队员施加额外的拉力，拉力沿绳方向。

由编号为0的队员施加额外的拉力 拉力沿绳方向。

综合鼓的位移和鼓面转动，列表给出队员们的不同发力时机和力度的策略：

由于编号为0和1的队员相比其他队员多用大约0.4N的力，且0.4N在总拉力中的占比约为十分之一，导致这两名队员对拉升的过程中多用的0.4N力感觉较明显。因此，这两名队员能够有意识地控制增加的力度，所以以上策略在实际情形中较容易实现。

四、模型检验与结果分析

本文中建立的模型所求出的结果符合客观事实，通过对比查阅同心鼓游戏项目相关的技巧，发现根据模型提出的策略与同心鼓游戏的实际经验相吻合，由此可见，本文中提出的模型是正确的。

问题一针对理想状态下的团队颠球策略，建立了每名队员发力随时间变化的周期函数，使得团队成员在尽可能省力的情况下，尽可能地保证项目不停止。问题2针对实际情况中鼓面的转动情况，建立了每名队员对绳的拉力与鼓面倾斜角之间的动态关系，通过matlab程序计算，可以快速得到鼓面的倾斜角度。根据问题2中的求得的数据对比可以发现，提前拉绳与同时拉绳相比，拉力大小不同，且對鼓面倾斜角的影响更大。问题3对问题1中的模型在现实背景下进行优化，得到更贴近现实情况的实用模型。问题4综合运用了问题1和问题2中的模型来解决角度修正的问题。

根据本文中各个问题的结果，最终得到以下几条“同心协力”游戏的技巧：

1.无论如何，一定要保证团队成员注意力高度集中，统一行动，尽可能保证 同时拉绳，可以让力气大小差不多的队员面对面，这样可以使鼓面尽可能保持水平。

2.颠球高度不宜过高，可以控制实际颠球高度约为最低高度的110%，以减小由于鼓面倾斜导致的球偏离鼓心的距离。

3.在发现球偏离鼓心位置时，处在球偏离方向的队员应该主动加大对绳的拉力，消除鼓面的倾斜角，尽可能保持球在竖直方向上运动。

参考文献：

[1]张三慧.大学物理学（第三版/C6版）上册[M].北京：清华大学出版社，2014年.

[2]杨克昌.均质圆柱类刚体对任意轴的转动惯量计算公式.力学与实践[J].1983年，05期：53-54.

[3]司守奎，孙兆亮.数学建模算法及应用（第二版）.北京：国防工业出社，2018年9月.

（作者单位：华北电力大学（保定）能源动力与机械工程学院）