你“随机”，我“应变”

张丽华

概率用于刻画“随机”事件发生的可能性大小。虽说事件“随机”，但随机事件的发生有迹可循、有法可依。在历年中考中，这一知识点常以选择题、填空题形式出现。现采撷几道相关试题，我们来体会应变之道。

“随机”问题一：区分“事件”类型

例1（2018·包头）下列事件中，属于不可能事件的是（）。

A.某个数的绝对值大于0

B.某个数的相反数等于它本身

C.任意一个五边形的外角和等于540°

D.长分别为3、4、6的三条线段能围成一个三角形

【解析】根据定义可知A、B为随机事件，

D为必然事件，故选C。

变式一（2015·徐州）一只不透明的袋子中装有4个黑球、2个白球，每个球除颜色外都相同，从中任意摸出3个球，下列事件为必然事件的是（）。

至少有1个球是黑球

• B.至少有1个球是白球
• C.至少有2个球是黑球
• D.至少有2个球是白球
• 【解析】由于只有2个白球，则从中任意摸出3个球，至少有1个球是黑球，故选A。

变式二（2018·淄博）下列语句描述的事件中，是随机事件的为（）。

A.水能载舟，亦能覆舟

B.只手遮天，偷天换日

C.瓜熟蒂落，水到渠成

D.心想事成，万事如意

【解析】根据定义分析得A、C是必然事件，B是不可能事件，因此选D。

【应变之法】事件分为确定事件和随机事

件。确定事件又分为必然事件和不可能事件。必然事件指在一定條件下，一定发生的事件。不可能事件指在一定条件下，一定不发生的事件。随机事件指在一定条件下，可能发生也可能不发生的事件。正确把握相关定义是区分“事件”类型的关键。

“随机”问题二：利用“频率”估计“概率”例2（2019·扬州）扬州某毛绒玩具厂对一批毛绒玩具进行质量抽检的结果如下：

从这批玩具中，任意抽取一个毛绒玩具是优等品的概率的估计值是。（精确到0.01）

【解析】由表中可见，当试验次数很大时，优等品的频率在0.92附近摆动，利用频率估计概率可判断任意抽取一个毛绒玩具是优等品的概率为0.92。

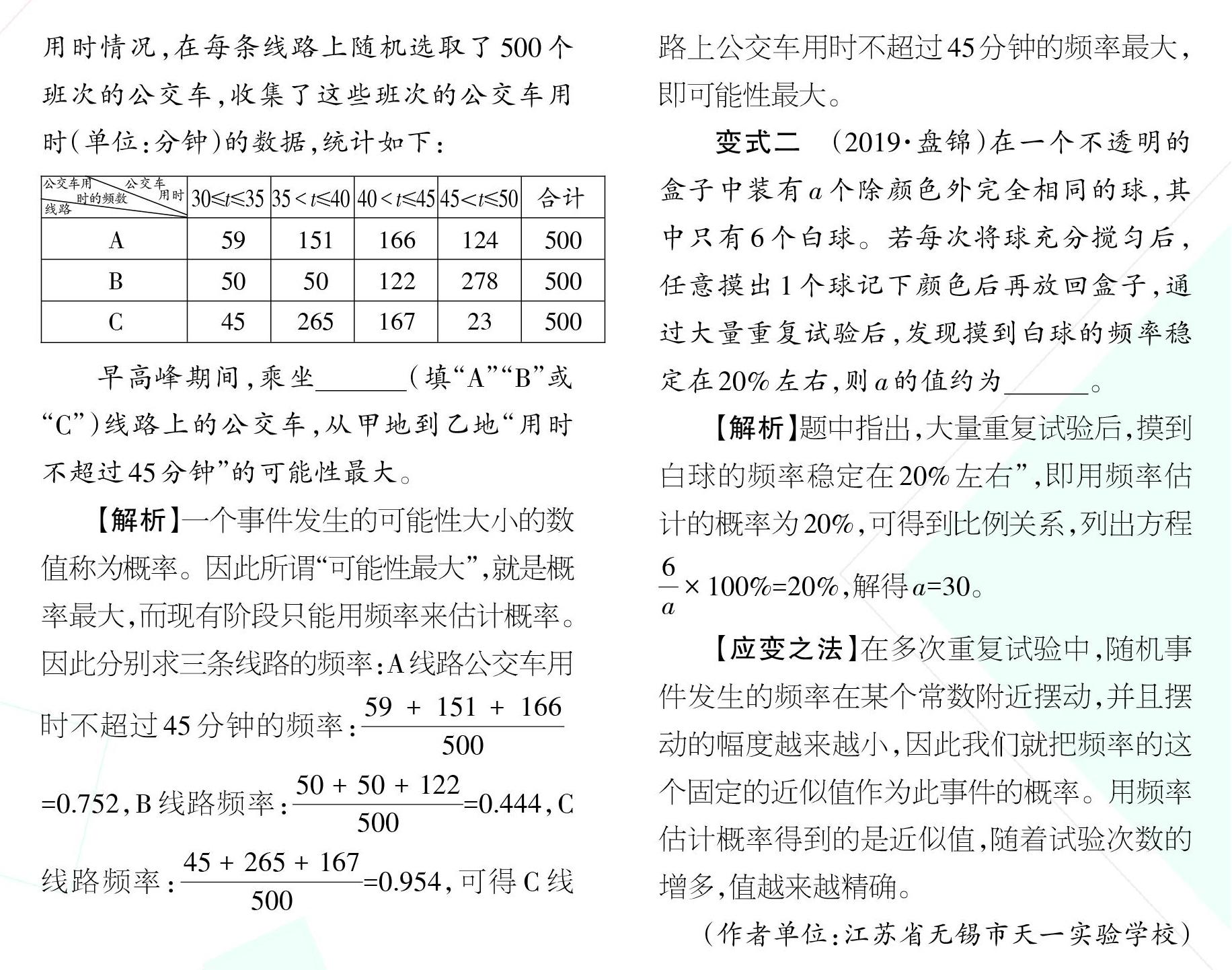
变式一（2018·北京）从甲地到乙地有A、B、C三条不同的公交线路。为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况，在每条线路上随机选取了500个班次的公交车，收集了这些班次的公交车用时（单位：分钟）的数据，统计如下：

早高峰期间，乘坐（填“A”“B”或“C”）线路上的公交车，从甲地到乙地“用时不超过45分钟”的可能性最大。

【解析】一个事件发生的可能性大小的数

值称为概率。因此所谓“可能性最大”，就是概率最大，而现有阶段只能用频率来估计概率。因此分别求三条线路的频率：A线路公交车用

59+151+166时不超过45分钟的频率：500

50+50+122=0.752，B线路频率：500=0.444，C

45+265+167线路频率：500=0.954，可得C线路上公交车用时不超过45分钟的频率最大，即可能性最大。

变式二（2019·盘锦）在一个不透明的盒子中装有a个除颜色外完全相同的球，其中只有6个白球。若每次将球充分搅匀后，任意摸出1个球记下颜色后再放回盒子，通过大量重复试验后，发现摸到白球的频率稳定在20%左右，则a的值约为。

【解析】题中指出，大量重复试验后，摸到白球的频率稳定在20%左右”，即用频率估计的概率为20%，可得到比例关系，列出方程6a×100%=20%，解得a=30。

【应变之法】在多次重复试验中，随机事件发生的频率在某个常数附近摆动，并且摆动的幅度越来越小，因此我们就把频率的这个固定的近似值作为此事件的概率。用频率估计概率得到的是近似值，随着试验次数的增多，值越来越精确。

（作者单位：江苏省无锡市天一实验学校）