受周边基坑施工影响的道路沉降预测研究

王 春

(江苏省基础地理信息中心，江苏 南京 210013)

1 概述

近年来，城市现代化的飞速发展使得城市道路、建(构)筑物以及地下工程将会密集型开发建设。未来的趋势是基坑工程的开挖建设会逐渐增多，在保证基坑的顺利开挖的同时，基坑施工造成周边道路的沉降现象越来越受到各方的关注[1]。目前已有的道路沉降预测研究方法包括:沉降曲线拟合法(双曲线法、指数曲线法、泊松曲线法、三点法、S型曲线法等);Asaoka方法;人工神经网络法;遗传算法;灰色预测法;有限元法等[2]，但是其中大多数预测方法无法模拟沉降数据的准确变化，预测结果难以满足精度要求，导致无法为工程提供参考价值[3]。区别于单一模型，组合模型综合利用了子模型的优势信息，进而可以更好地用于建筑物的沉降预测[4]。本研究基于幂函数、多项式函数及BP神经网络建立了一种新的组合预测模型。

2 组合模型的建立

采集实测沉降数据，提取监测时间x及沉降观测值y，并按时间顺序分为两部分：由j个点组成的学习数据、由k个点组成的验证数据。

2.1 建立幂函数预测模型

利用学习数据建立如下模型[5]：

(1)

式中：x——监测时间;

y——沉降实测值;

p——沉降预测值;

a,b,c——模型系数。

2.2 建立多项式预测模型

利用学习数据建立如下模型[6]：

(2)

其中，a0,a1,…,an为模型系数。

按时间的递增，自j开始，逐步增加拟合数据的个数，即：以1为增幅逐步减少n值，并计算多项式拟合曲线的相关系数r，其中，相关系数r的计算公式为：

(3)

当n=N(N≤j)时,若rN-rN-1的值不大于10-3，停止计算且取n=N为多项式的次数。

2.3 建立BP神经网络预测模型

BP神经网络是基于误差反向传播算法的多层前馈型神经网络，有研究表明，三层神经网络模型就可以解决一般的函数拟合逼近问题，BP神经网络的过程主要分为两个阶段，第一阶段是信号的前向传播，从输入层经过隐含层，最后到达输出层；第二阶段是误差的反向传播，从输出层到隐含层，最后到输入层，依次调节隐含层到输出层的权重和偏置，输入层到隐含层的权重和偏置[7]。

2.4 建立组合模型

计算三个子模型预测值的标准差绝对值之和：

J=|J1|+|J2|+|J3|

(4)

其中，J1,J2,J3分别为幂函数模型、多项式模型及BP神经网络模型预测值标准差。

幂函数模型、多项式模型、BP神经网络模型的权值可分别由下式计算：

(5)

其中，l1,l2,l3分别为幂函数模型、多项式模型、BP神经网络模型的权。

由上式所得权值，建立组合模型：

Pi=[l1,l2,l3][p1i,p2i,p3i]T

(6)

其中，Pi为i时刻组合模型的预测值。

3 计算与验证

分别利用幂函数模型、多项式模型、BP神经网络模型对道路的沉降观测值进行拟合，经分析与计算，建立幂函数模型如下：

(7)

建立多项式模型如下：

(8)

道路沉降主要由基坑沉降造成，本文建立隐含层(Hidden)有10个连接节点的三层BP神经网络模型，如图1所示，输入(Input)数据采用道路的沉降监测期数及所对应的周边基坑沉降监测值，输出层(Output)采用道路的沉降监测值。

三种模型的拟合效果如图2～图4所示。

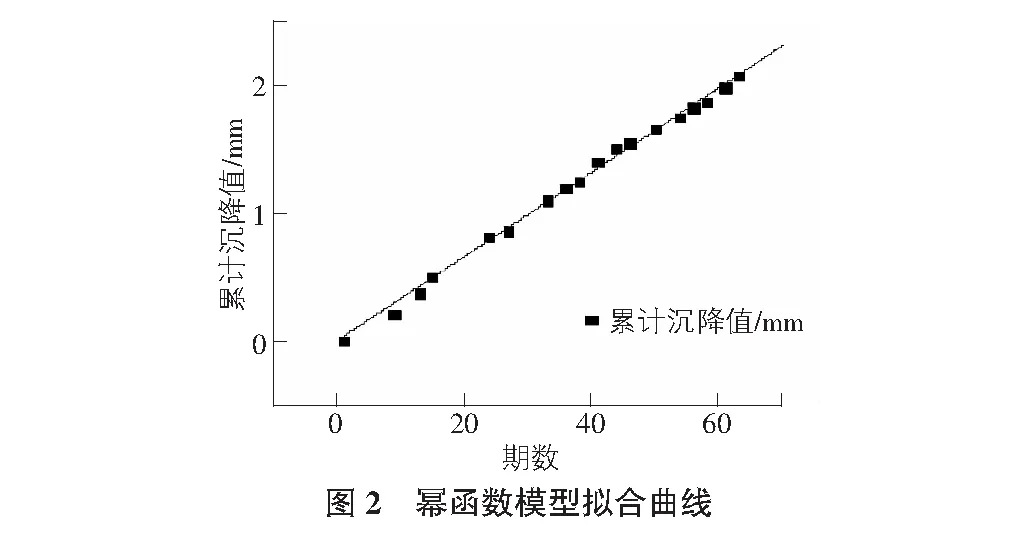
幂函数模型、多项式模型及BP神经网络模型拟合的精度如表1所示。

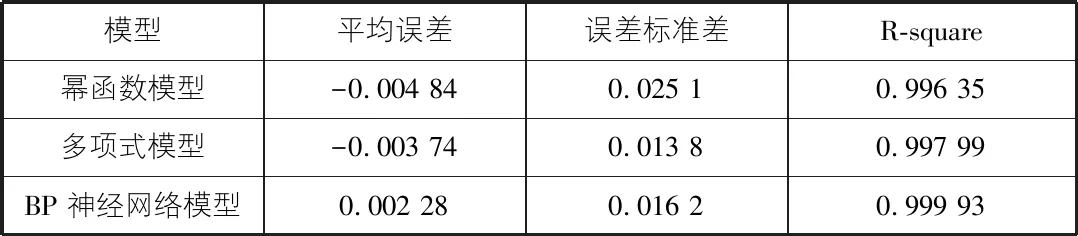
表1 三种子模型的拟合精度

表1中，R-square(确定系数)的取值范围是[0，1]，越接近1，表明模型对数据的拟合程度更好。

基于前文所述组合模型的建立方法，通过计算三种子模型的预测值标准差，得到组合模型的权重系数，从而得到组合模型：

Pi=0.455 535p1i+0.250 454p2i+0.294 011p3i

(9)

利用三种子模型与组合模型分别对一组验证数据进行预测，并分别计算其预测误差，其结果的均方根如表2所示。

表2 四种模型的精度验证

从四个模型的RMSE来看，组合模型的精度优于单项预测模型，说明组合模型是一种精度更高的预测方法。

4 结语

本文根据某道路的沉降监测实例，分析并建立了幂函数模型及多项式模型，并利用周边的基坑沉降数据建立了道路沉降BP神经网络模型，根据各模型的预测精度，确定了三个子模型在组合模型中的权重，并最终建立了组合模型，利用沉降监测数据对四个模型进行了精度检验，结果表明，组合模型拥有更高的精度，可以用于基坑沉降预测。