MC模型与SSC模型在数值模拟中的对比分析

2020-06-20徐海波

山西建筑 2020年13期

徐海波吴杰

(1.安徽省(水利部淮河水利委员会)水利科学研究院，安徽蚌埠 233000；2.安徽省建筑工程质量监督检测站，安徽合肥 231000)

1 概述

土体本构模型是开展土体数值计算的重要依据，没有本构模型就不可能客观反映土体的应力应变关系，数值计算就无从谈起。目前，国内外学者针对不同土体提出了线弹性模型、邓肯—张(DC)模型、摩尔—库仑(MC)模型、Drucker-Prager模型、修正剑桥模型、软土蠕变(SSC)模型等多种模型[1，2]。不同的模型只能反映一种或几种土体的基本性质，应用的范围具有一定的局限性。

河堤公路依河堤而建，路基大部分为历史形成的土堤。鉴于当时勘察技术和施工机具的落后，土堤填筑前很少做专业的细致勘察，即使查明地基中含有软土层，也因技术限制或赶工期等因素未作彻底处理。河堤公路拓宽时，老路基经过几十年的固结已达到稳定。拓宽后，新拓宽段在上部荷载的作用下，新路基产生较大幅度沉降；老路基由于新填土的影响产生附加沉降，但影响程度远小于新路基段，因此老路基产生的附加沉降小于新路基沉降。另外地基中的蠕变性土层，使新路基产生较大的工后沉降，并随时间的增长沉降增大，加上新老路基固结度不同等因素，使新老路基之间产生不均匀变形[3-5]。因此，在河堤公路的数值计算中如何选取合适的本构模型真实反映路基、路面的位移变化显得十分必要。本文选取常用的MC模型、SSC模型，通过某河堤公路工程，分析两种MC模型、SSC模型的特点和不足，研究成果对类似河堤公路数值模拟计算提供借鉴。

2 工程背景

某河堤公路建于20世纪30年代，部分路段由河堤改造而成。路面宽15 m，其中老路面宽7 m，拓宽新路面宽8 m；路基高7 m，背水面路基坡度为1∶1.3，迎水面路基边坡为1∶1.5，河水位为4.0 m。道路扩宽时，由于河水的影响，扩宽只能选取河堤背水面，即拓宽形式为非对称式单侧扩宽，如图1所示。

通过室内试验，证实地基中③层土具有蠕变特性，该土层厚5 m，计算中该土层土体模型分别选用Plaxis程序中MC模型和SSC模型，地基中其他土层均采用MC模型，路基和地基的土层参数见表1。

为表述方便，在模型中设置A，B，C，D，E，F，G七个特征点，分别代表新路基坡脚处地表点(40,31)、老路基坡脚处地表点(48,31)、老路基中心地表点(62,31)、老路基临河侧坡脚点(84,27)、路面左边缘点(49,38)、路面新老路基结合处(57,38)、路面右边缘点(64,38)。

表1 路基和地基的土层参数

参数老路基新路基地基23456材料模型M-CM-CM-CM-CSSCM-CM-CM-C天然容重/kN·m-318.018.317.218.018.017.51716.8饱和容重/kN·m-320.020.319.019.619.619.318.519.5水平渗透系数/cm·d-14.04.00.050.010.014.70.010.01竖向渗透系数/cm·d-14.04.00.050.010.014.70.010.01弹性模量/kPa6 7007 5004 0006 00010 0004 5005 600泊松比0.30.30.150.290.290.30.30.3内粘聚力/kPa36.620.7193030827.451.4内摩擦角/(°)22.524.81717172723.225.1修正压缩指数————0.09———修正膨胀指数————0.008 9———修正蠕变指数————0.002 9———

3 有限元计算准备

3.1 网格划分及边界条件

采用Plaxis软件进行有限元计算，单元形式采用6节点三角形单元，程序根据边界条件自动划分单元。为减小边界的影响，地基厚度取31 m，宽度取140 m，模型左右边界上不发生水平位移，不排水，设置隔水边界；下边界水平和竖向位移都不发生，排水；上边界为自由边界，排水。

3.2 初始条件及加载历程

公路拓宽前，已经过四五十年的固结，地基和路基均已固结完毕，路基达到了稳定状态，计算时间从新路基填筑时开始，老路基和地基共同构成了模型计算的初始应力，应力生成方式为重力加载。新路基共分7层填筑，每层1 m，填筑速率每层30 d，填筑完毕固结100 d后加铺路面，至路基固结31年，加载历程见图2。为方便比较M-C模型与SSC模型计算成果，计算中河水位(取常水位)和地下水位均保持不变。

4 计算结果分析

4.1 路基变形特点

4.1.1地基地表沉降

图3为M-C模型和SSC模型的地表沉降曲线。

1)共同点：两种模型计算的最大地表沉降均位于新老路基结合处；新路基对整个老路基均有影响，并从新路基至运河方向逐渐减小；拓宽工程仅对坡脚以外20 m内的地表有影响，尤其对坡脚10 m以内区域影响较大。

2)不同点：新路基竣工后，SSC模型中B,C两点的沉降值小于M-C模型计算，减小值分别为1.2 cm和0.7 cm；而A,D两点沉降略有增加，分别为0.3 cm和0.1 cm。SSC模型的地表总沉降大于采用M-C模型的计算结果，说明土体蠕变使地表沉降增加。

3)工后沉降：SSC模型地表特征点的工后沉降大于M-C模型的结果。M-C模型中A,B,C点的工后沉降为1.7 cm,1.7 cm,1.8 cm，占总沉降的10%左右，说明土体采用M-C模型，路基沉降主要在施工期及固结期内，公路运营期间路基沉降较小，路面出现纵向裂缝的概率较小。SSC模型下A,B,C点的工后沉降分别为4.4 cm,6.6 cm,5 cm，占总沉降的20%以上，说明竣工后路基仍存在较大次固结沉降，路基的不均匀工后沉降是运营期内公路产生纵向裂缝的主要原因。

4.1.2路面位移

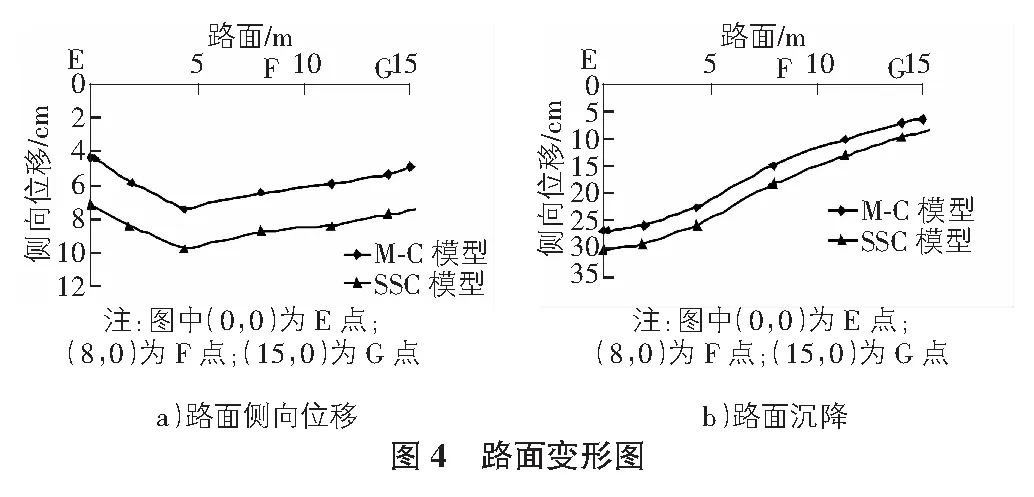
图4为路面位移变化图。

根据图4可知，路面最大沉降位于路面左路肩处，采用SSC模型的路面沉降和侧向位移均大于M-C模型计算结果。两种模型路面沉降最大值分别为26.8 cm,30.3 cm；最大侧向变形位于新路基侧左边缘4 m处，分别为9.7 cm,7.4 cm；两种模型的路基沉降差大致相同，路基横坡比分别为1.36%(M-C模型)、1.5%(SSC模型)。

4.1.3坡脚位移

图5，图6分别为坡脚的侧向位移和沉降。

根据图5,图6，坡脚地表下13 m内的区域，采用SSC模型所得的侧向位移和沉降均大于M-C模型的计算结果，其中老路基坡脚最大侧向变形和沉降比M-C模型分别增大246%和14.7%；新路基坡脚最大侧向变形和沉降比M-C模型增大105%和26.5%，可见地基中的蠕变土层对坡脚侧向位移影响显著，最大位移位置向地基深处发展；图中，蠕变土层下方，两种模型的侧向位移方向不同。M-C模型侧向位移向新路基方向移动，而SSC模型侧向位移向老路基方向移动；蠕变土层引起的新路基坡脚沉降大于老路基坡脚。坡脚地表下13 m以外的区域，两种模型的计算结果大致相同。

4.2 地表特征点时间—沉降曲线

图7是B点时间—沉降计算结果与实测相关对比图。观测时间不是从路基的填筑开始的，观测时路基已运营了一段时间，本文利用同一位置沉降与时间的相关性(即同一点沉降的发展趋势)来分析M-C模型和SSC模型的适用性。从图7中可知，实测D点沉降随时间的发展趋势与采用SSC模型较为接近，因此，采用SSC模型是合适的。