土地整理项目选址决策支持系统设计与实现

王华 张杰

摘  要： 基于多目標群智能算法设计并实现一个开放、智能的空间辅助决策支持系统，为我国的土地整理实践工作提供科学合理的决策支持。研发了插件式的土地整理项目选址智能决策支持系统，在该系统框架下实现了对土地整理项目区土地利用现状分析、土地整理适宜性评价、智能选址等功能。将所提系统应用于湖北省嘉鱼县进行实例验证，结果表明该系统在土地整理工作实践中具有实用价值。

关键词： 选址决策支持系统; 土地整理项目选址; 群智能算法; 土地利用现状分析; 土地整理适宜性评价; 智能选址; 系统价值验证

中图分类号： TN99?34; F301.2                      文献标识码： A                    文章编号： 1004?373X（2020）09?0179?04

Design and implementation of decision support system

for land consolidation project location

WANG Hua， ZHANG Jie

（School of Computer and Communication Engineering， Zhengzhou University of Light Industry， Zhengzhou 450002， China）

Abstract： An open and intelligent spatial aided decision support system is designed and implemented based on the multi?objective swarm intelligence algorithm to provide scientific and reasonable decision support for land consolidation practice in China. A plug?in intelligent decision support system for location of land consolidation projects is developed. In this system， the functions of the situation analysis of land use， land consolidation suitability evaluation and intelligent location in the land consolidation project area are achieved. The proposed system was applied in Jiayu county in Hubei province for verification. The results show that the system has practical value in land consolidation practice.

Keywords： decision support system for location; location of land consolidation project; swarm intelligence algorithm; land use situation analysis; land consolidation suitability evaluation; intelligent location; system value verification

0  引  言

土地整理项目选址是将土地整理项目的实施区域在空间范围内予以具体落实的一项工作任务，其科学合理性是土地整理项目实施成败的先决条件。现有研究重点分析了地形地貌、土壤质量、气候、交通可达等自然、社会经济因素对土地整理项目选址的影响[1]，也有部分学者从定量的角度探讨利用层次分析法、特尔斐法等方法对土地整理项目的可行性进行评价，以检验前期项目选址的科学性[2?4]。上述研究和方法在解决具体的土地整理项目选址问题时虽具有一定的辅助作用，但由于缺乏统一、科学的土地整理项目选址理论及方法体系支撑，导致地方政府在土地整理项目的选址上具有一定的盲目和随意性，出现项目土地适宜性程度低、空间布局零碎等问题，难以充分发挥土地整治综合效益。可将土地整理项目选址问题看作一个多目标空间优化问题[5]。近些年人工智能和GIS技术在空间选址、土地资源优化配置等方面获得较多应用[6?10]。针对我国土地整理工作决策支持的实际需求和土地整理项目选址研究现状，本文基于多目标群智能算法模型，设计了面向土地整理项目选址问题求解的通用算法模型框架。为相关研究及工作人员提供了一个开放、智能的空间辅助决策支持系统，为我国的土地整理实践工作提供了科学合理的决策支持。

1  土地整理项目选址决策需求分析

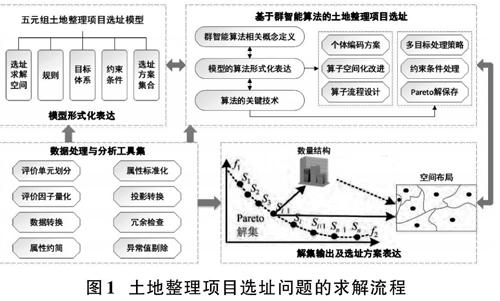
本研究将传统土地整理项目选址问题抽象为一个多目标空间优化决策问题，并借助计算机技术、3S技术为其提供一个智能决策支持平台。该平台主要依据土地整理项目选址问题的求解流程来设计与实现，如图1所示。

土地整理项目选址需重点考虑以下四个问题：

1） 选址问题形式化表达。本研究将土地整理项目问题抽象为一个五元组模型：

[LMLCP=（S，R，O，C，POS）]

式中：LMLCP（Location Model of Land Consolidation Project）代表土地整理项目选址模型;S（Space）表示选址模型的求解空间;R（Rule）表示选址模型的规则;O（Object）代表选址模型的目标;C（Constraint）为选址模型的约束条件;POS（Pareto Optimal Set）表示选址模型的非劣解集合。

在本模型中，利用矢量图斑的形式来表达土地整理选址的决策空间，每一个矢量图斑均为一个决策单元，决策单元的取值由是否被划进项目区来决定，即0或1。选址模型的规则、目标体系、约束条件则是对土地整理项目选址影响因素的分析，将对影响因素的一些定性描述转化为可量化计算的定量描述。本研究选择最大新增耕地潜力、最佳土地整理适宜性和最大空间紧凑度为优化目标。在决策单元划定时还需考虑一些约束条件，如项目区规模及新增耕地率指标，遵循的规则需要考虑土地利用类型、地形、道路通达等因素。选址模型的非劣解集合是指能够使决策者既定的多个目标均获得较好满足的解集合，可通过多目标决策方法获得，每一个非劣解均代表一个土地整理项目选址方案。

2） 多目标群智能求解算法。群智能算法创造了被称为种群的潜在解集合，算法通过种群中个体之间的相互通信、协作与竞争机制实现对求解问题最优解的搜索，往往具有比传统优化算法更迅速地搜索问题最优解的能力。本研究提出应用常见的粒子群（PSO）和人工蚁群两类群智能算法求解LMLCP模型，通过定量化、智能手段为决策者提供不同决策偏好的选址方案。利用多目标优化技术研究构建面向土地整理项目的基于粒子群、蚁群算法的空间选址优化模型，需将算法基本概念、演化机制与土地整理项目空间选址具体问题进行结合，基于具体问题的求解空间进行粒子、人工蚂蚁的个体编码方案设计，在此基础上再继续进行粒子生成、粒子状态更新、蚂蚁选择、信息素更新核心算子的构建。

3） 选址方案可视化表达。本系统将GIS可视化技术与智能方法结合，对个体所代表的空间布局方案进行解译表达，便于分析校验优化结果及決策支持。该功能主要包含两个步骤：首先，将经过Pareto排序后推荐的最优解进行解译，基于个体编码方案将其反向映射为矢量决策数据层的属性结构表;其次，基于该属性结构，利用GIS制图接口实现该数据层的符号化及分类渲染，并配备相应图例、图框等专题图要素，为用户提供标准的土地整理项目选址方案专题图。

4） 数据处理与分析。本系统借助GIS强大的空间数据处理能力整合多源异构数据，利用GIS数据管理接口来实现空间决策单元划分、评价因子量化、数据转换、数据清理、数据标准化等功能模块，为LMLCP模型提供数据支撑，并在模型运算过程中提供叠加分析、邻域分析、多边形面积统计等空间分析技术，保障模型对海量空间、属性数据的高效处理。

2  系统设计

2.1  系统架构

系统开发的基本目标在于为土地整理项目选址模型研究者和相关决策者提供一个开放的智能软件平台，以提高土地整理项目选址决策水平。本研究在“数据层?业务层?应用层”三层框架基础上采用“ 宿主?插件” 模式进行系统架构设计，主要包含数据引擎、支撑类库、功能插件库、优化算子库、宿主程序、应用层6个组成部分，如图2所示。

1） 数据引擎：利用空间数据库引擎ArcSDE和属性数据访问引擎ADO.NET来实现辅助土地整理项目选址决策的海量空间、属性数据的一体化存储、管理和访问。

2） 支撑类库：包括系统实现所必须的核心组件库如.net framework，ArcEngine以及为插件扩展开发所定义的基本工具接口、算子接口、优化问题接口等。

3） 功能插件库：由土地整理项目选址模型工作者基于基础接口开发的一系列功能算子插件，为特定模型提供数据处理分析功能。

4） 优化算子库：由群智能算法研究者基于基本算子接口开发的一系列粒子状态更新、蚂蚁选择、信息素更新改进算子，用于实现群智能算法不同的进化操作。

5） 宿主程序：在插件式框架中，宿主程序是一个独立运行的exe程序，作为系统框架的运行入口，可通过人机交互方式实现项目选址优化问题及求解模型的定义，宿主程序根据用户预先定义好的参数配置及模型流程，动态调用所需应用插件及算子插件，执行优化任务并输出优化方案。

6） 应用层：也即系统的主要功能，包括土地整理区的土地利用现状统计分析、适宜性评价、基于不同群智能算法的土地整理项目选址优化决策等内容。

2.2  数据库设计

土地整理项目选址是一个需要海量数据支持的复杂空间决策问题，整个决策过程会涉及到遥感影像、土地利用现状等各种空间数据，以及社会经济等属性数据。因此，为使繁杂的多源异构数据能够服务于土地整理项目选址的科学决策，必须依托类似Oracle这种大型数据库管理系统结合ArcSDE空间数据库引擎实现对时空数据的一体化存储管理，并且必须制定逻辑结构清晰的数据存储方案。所以本研究根据数据要素的同源性，在数据库整体框架的基础上将全库划分为以下逻辑子库：

1） 基础地理信息库：主要采用矢量FeatureClass数据模型存储行政区边界、等高线、流域等基本要素信息;

2） 土地利用数据库：该库主要为矢量空间数据，同样，采用Featclass数据模型存储土地利用图斑、线状地物、点状地物等土地利用信息，是土地整理项目选址需要依据的基础数据;

3） 影像库：主要以栅格数据模型（RasterDataSet）存储包含高程、坡度等能够反映地区地形地貌信息的影像数据;

4） 土地利用规划库：该库主要为土地利用规划、生态保护区、军事敏感区以及规划文本、指标等信息;

5） 土地整治专项规划库：包括对规划区内的土地利用整理潜力分析数据、规划文本、各类规划图件等数据;

6） 社会经济统计数据库：主要包括当地的GDP、人均收入、财政收入、基础设施建设等数据，这些因素能够显著影响土地整理项目选址;

7） 评价因子库：主要存储土地利用单元的整理适宜性评价因子，以及各因子所对应的空间图层;

8） 选址知识库：项目选址时需要遵循一定的规则，并满足必定的条件，在数据库中可以将这类知识信息予以存储，便于选址模型调用;

9） 系统数据库：主要以关系表模型存储系统用户、各类数据字典、各类业务流程等与系统管理密切相关的数据信息。

2.3  功能结构设计

为给土地整理项目选址决策提供方便、科学的数据处理、统计分析工具以及决策模型，本文将系统功能划分为5个一级模块，21个二级模块，工程管理模块集成于宿主程序内，其余模块则以插件形式分别实现。

1） 工程管理：在系统中以工程的形式管理项目选址工作，每一个工程中需要包括涉及到的项目名称、指标、数据、模型参数等信息。

2） 数据管理：土地整理项目选址涉及到大量的空间、属性数据，因此，本模块为系统提供了数据导入、管理的接口，并基于数据挖掘思想提供了包括属性约简、标准化、异常数据剔除等数据处理模块。

3） 土地利用分析：该模块主要是为了便于决策者了解规划区域的土地利用现状，包括对土地利用结构、程度以及整理潜力的分析。

4） 土地整理评价：根据土地适宜性评价的工作流程，在评价单元划定、因子选择、因子量化等功能模块支撑下，系统还提供了基于综合加权、系统聚类以及自组织特征映射神经网络（SOM）的评价模型，为土地整理项目选址决策提供重要依据。

5） 项目选址模型：该模块为系统的核心模块，本研究将常见的粒子群算法、蚁群算法（ACO）原理与多目标土地整理项目选址优化问题特性相结合，构建求解LMLCP模型的群智能进化框架，改进个体编码及优化算子，在系统中分别实现了面向土地整理项目选址优化决策的粒子群模型、蚁群模型及粒子群?蚁群混合模型。

3  系统实現与应用

根据以上设计，本研究在Visual Studio.NET 2010开发平台支持下，选用第三方控件集合DevExpress和ArcEngine 10.0 GIS组件集合来设计系统宿主程序以及各功能插件的UI，最终得到如图3所示的系统界面。

选取湖北省嘉鱼县为实验区，以粒子群?混合蚁群混合模型为例，进行本系统的实效性验证。实验数据包括第二次土地调查数据、坡度、DEM等空间信息数据、土地整理适宜性评价结果和人口、GDP等社会经济数据。

该混合模型的基本改进思想是利用PSO算法来优化ACO的基本参数，因此ACO算法的[m]，[α]，[β]和[ρ]四个参数不需要设置，而信息素强度[Q]，初始信息素[τ0]，最大迭代次数[TA_max]则借鉴已有的研究来设置，令[Q=]100，[τ0=]0.1，[TA_max=]100。在上述参数设置下运行粒子群?混合蚁群模型，并利用并列选择法进行多目标处理，将外部档案中所有非劣解绘制如图4所示的散点图。由于土地整理项目模型中的目标函数均是求取最大值，因此，在散点图中所有点的取值为原目标函数值的倒数，模型中的最大新增耕地潜力目标（EB）、最佳土地整理适宜性目标（ST）和最大空间紧凑度目标（AD）如图4所示位置。其中，黑色点是根据非劣解之间的支配关系所选取Pareto解集，并形成Pareto前沿，从中挑选一个Pareto解，将其解码为空间选址方案，如图5所示，从数量和空间结构的角度来分析嘉鱼县土地整理项目选址结果特征。

系统在模型运行前已经根据选址规则对土地利用类型为建设用地、水域的空间单元进行特殊的处理，人工蚁群在模型迭代过程中可以直接排除这类用地单元，在最终的选址方案中将这类用地划分进非整理区。

由于人工蚁群算法采用的随机选择机制使得被选中土地单元呈现较为零散的空间布局，模型在综合考虑空间集中连片目标及约束规模的情况下，土地整理项目选址方案中仍出现了部分不满足项目规模约束条件的片区。但从图5可以看出，嘉鱼县土地整理项目选址方案总体空间格局在簰洲湾镇等乡镇已呈现出明显的空间聚集。

选址方案中各乡镇的可整理面积的统计结果见表1。潘家湾镇备选整理区面积达到6 300 hm2左右，其可整理潜力最大;簰洲湾镇次之，可整理面积接近5 900 hm2，作为嘉鱼县的主要农业生产镇，这两个乡镇地形起伏较缓、水资源条件丰富，但受限于农用地整体规模不足，局部空间格局散乱;鱼岳镇作为嘉鱼县政治经济文化中心，受城镇人口增加、城镇用地扩张等原因，其可整理规模最小。从新增耕地率来看，新街镇达到5%为最高;官桥镇与潘家湾镇次之，且均达到4%。结合土地利用现状来分析，这几个镇地块面积较小，且农地之间零星废弃闲置用地分布也较多。

对选址方案综合统计可以看出，全县规划期内共有约2.57万公顷的农用地及零星废弃闲置用地可以进行整理，通过平整土地、归并零散地块、改良土壤、完善道路、林网、沟渠等综合建设等方式，预计可新增耕地1 043.75 hm2，嘉鱼县重点整治区域主要包括官桥镇、潘家湾镇、新街镇、簰洲湾镇等。

4  结  论

本文通过对土地整理项目选址问题进行分析研究，将其归纳为一个多目标五元组空间优化模型。设计面向该问题模型的群智能求解算法框架，并将人工智能与GIS和计算机技术相结合，详细阐述了系统的插件式框架实现思路、基于空间数据引擎的多源异构数据一体化存储方案和功能模块结构设计。系统在嘉鱼县的应用结果表明：系统能够基于标准的多目标群智能模型框架来选择不同的进化算子进行选址方案的优化决策，使其能够在多个目标上尽量最优，并能够为用户提供多样化的非劣解以满足决策者的不同偏好。该决策支持系统能够为相关工作研究人员提供一个开放式的土地整理项目空间优化选址问题求解平台，进而推进多目标群智能算法在空间优化选址问题研究领域中的应用，提高土地整理实践工作决策的科学合理性。

参考文献

[1] 杨丽娜，何星，杨庆媛，等.土地综合整治项目选址影响因素分析[J].资源开发与市场，2017（3）：289?294.

[2] 任艳敏，徐亚辉，刘玉，等.基于双重自组织模型的土地整治项目区时空配置研究[J].北京大学学报（自然科学版），2017，53（2）：360?368.

[3] 樊鹏，邵红旗，杨青伟，等.基于耕地质量评价的土地整治项目选址研究：以河南省延津县为例[J].湖北农业科学，2017（16）：3037?3041.

[4] 洪開荣，刘欢，王辉.直觉语言多准则决策方法在土地整理项目社会效益评价中的应用[J].经济地理，2015，35（7）：163?167.

[5] 王华，朱付保.基于多目标粒子群的土地整理项目选址模型[J].农业工程学报，2015，31（14）：255?263.

[6] LIU Xiaoping， LI Xia， TAN Zhangzhi. Zoning farmland protection under spatial constraints by integrating remote sensing， GIS and artificial immune systems [J]. International journal of geographical information science， 2011， 25（11）： 1829?1848.

[7] LI Xia， LAO Chunhua， LIU Xiaoping. Coupling urban cellular automata with ant colony optimization for zoning protected natural areas under a changing landscape [J]. International journal of geographical information science， 2010， 25（4）： 575?593.

[8] ELDRANDALY K. A GEP?based spatial decision support system for multisite land use allocation [J]. Applied soft compu?ting， 2010， 10（3）： 694?702.

[9] 牛继强，徐丰.利用克隆选择算法构建的土地用途分区模型[J].武汉大学学报（信息科学版），2014，39（2）：172?176.

[10] 王华，刘耀林，姬盈利.基于多目标微粒群优化算法的土地利用分区模型构建[J].农业工程学报，2012，28（12）：237?244.

[11] TOKSARI MD. Ant colony optimization for finding the global minimum [J]. Applied mathematics and computation， 2006， 176（1）： 308?316.