基于多前车最优速度与加速度的网联车跟驰模型
2020-06-19史昕纪艺赵祥模惠飞
史昕 纪艺 赵祥模 惠飞
摘 要: 考虑车辆跟驰存在的延时性与传递性,基于网联车的智能感知与协同交互,提出一种基于多前车最优速度与加速度的网联车跟驰模型,并利用线性稳定性分析方法推导所提出模型的临界稳定性判别条件。以环形道路车队过程施加扰动为例,根据加速度敏感系数[ωi]和多前车数[k]设计数值模拟实验,结合速度和车头距等参数分析不同[ωi]和[k]取值条件下的车队行驶稳定性。模型稳定性分析表明,所提出模型在引入多前车最优速度与加速度项后,具备更优的稳定区域,且考虑前车数[k]越多、加速度敏感系数[ωi]越大,则模型的稳定性越好。数值模拟分析表明,所提出模型相比FVD,OVCM和MHOV模型,当加速度敏感系数[ωi]和前车数[k]取值合理时([ωi=0.3]且[k=4]),车队速度和车头距的波动幅度相对较小,由此说明所提出模型能较好地吸收扰动且有利于增强车队行驶稳定性。
关键词: 网联车跟驰模型; 多前车最优速度与加速度; 临界稳定性判别; 模型稳定性分析; 数值模拟分析; 扰动吸收
中图分类号: TN92?34 文獻标识码: A 文章编号: 1004?373X(2020)09?0135?06
Car?following model of connected vehicles based on
multiple optimal velocities and accelerations
SHI Xin, JI Yi, ZHAO Xiangmo, HUI Fei
(School of Information Engineering, Changan University, Xian 710064, China)
Abstract: In view of the characteristics of delay and transitivity of car?following, an MOVA?based (multiple optimal velocities and accelerations) connected vehicle car?following model is proposed on the basis of the perception and cooperative interaction of connected vehicles, and the critical stability criteria of the proposed model are derived with the linear stability analysis method. Taking the disturbance imposed by the car?following process of vehicle group on the circular road as an example, the numerical simulation experiment is designed with the reference of the acceleration sensitivity coefficient [ωi] and the number [k] of multiple proceeding vehicles, and the driving stability of the vehicle group under different selected values of [ωi] and [k] is analyzed in combination with the parameters of speed and headway. The results of stability analysis shows that the proposed model has a better stability region after introducing the MOVA, and the greater the number [k] of proceeding vehicles and the greater the acceleration sensitivity coefficient [ωi], the better the model stability. The analysis of numerical simulations indicates that, when the selected value of acceleration sensitivity coefficient [ωi] and the number [k] of proceeding vehicles are reasonable ([ωi=0.3] and [k=4]), the fluctuation range of the vehicle group speed and headway of the proposed model is relatively small in comparison with the models of FVD, OVCM and MHOV. Therefore, the proposed model can better absorb the disturbance and enhance the stability of vehicle group.
Keywords: car?following model of connected vehicle; MOVA; critical stability determination; model stability analysis; numerical simulation analysis; disturbance absorption
0 引 言
交通拥堵问题对人类生活和社会运行具有重要影响,为了解决日益严重的交通拥堵问题,国内外相关学者围绕车辆的跟驰建模展开大量的研究工作。车辆跟驰模型主要用来描述限制超车单行道上行驶车队相邻车辆间的相互作用,通常利用动力学方法研究前导车运动状态变化所引起跟驰车的相应行为,并以数学模型表达跟驰过程中各种状态参数的演变情况,是交通流仿真的核心基础理论[1]。
典型的研究成果主要有:早期提出的车辆跟驰模型存在不能准确描述实际交通场景中加速度的现象[2],为了解决这一问题,Chandler和Newell根据前后车的速度差和车间距建立基于刺激?反应的跟驰模型;Bando等围绕Newell所提出的模型,提出了一种基于前后车车间距的最优速度模型OV(Optimal Velocity),该模型具有简单和方便数值模拟等优点,但存在加速度异常的情形[3]。Helbing等针对OV模型未考虑前后车速度差所引起的加速度不合理问题,提出了一种广义力(General Force,GF)模型,当跟驰车的速度大于前车时,引入前后车负速度差修正OV模型以维持合理的车间距,但是没有考虑正速度差对跟驰车加速度的作用[4]。Jiang等考虑正负速度差对跟驰车加速度的影响,改进GF模型,提出了一种全速度差(Full Velocity Difference,FVD)模型,该模型可以较为全面地描述车辆跟驰行为,但是在维持交通流稳定性方面依然存在局限性[5]。Peng等考虑最优速度关于时间的差值项改进FVD模型,提出了一种基于驾驶员记忆的最优速度(Optimal Velocity Changes with Driving Memory,OVCM)模型,通过引入最优速度记忆项差值,使得OVCM模型在交通流稳定性方面优于FVD模型[6]。
以OVCM模型为例,在不考虑前车加速度的情形下,若前车速度小于跟驰车速度,相应地,跟驰车的加速度呈现减小趋势;若前车处于加速阶段,跟驰车需要借助前车速度信息并历经一定的时间延迟才能捕获车间距增大趋势,且在延迟时间段内跟驰车的加速度仍将继续减小。同时,在仅考虑单个前车最优速度的情形中,跟驰车只能根据单个前车进行速度调整,若考虑的前车采用先加速后减速,那么跟驰车的速度将呈现较大的波动,波动的主要原因是跟驰车所考虑的前车同样会受到自身前车速度变化的影响,但是跟驰车不能捕获所考虑前车的前车速度变化,从而引发跟驰车的速度出现过调。在实际驾驶环境中,如果考虑的前车速度小于跟驰车速度且处于加速状态,则跟驰车的加速度不会立即减小,甚至在保证安全车头距的情况下适当地给予增加;如果考虑的前车速度小于跟驰车速度且小于自身的前车速度,跟驰车的速度会在保证安全车头距的情况下适当地给予减小,也有可能不采取减速措施。因此,考虑引入多前车行驶状态来有效吸收车队中多前車行驶状态突变引发的扰动,从而提升交通流的稳定性。
在智能网联环境中,跟驰车利用车载终端和无线通信可以获取多辆前车的行驶状态信息,如车头距、速度、加速度等[7]。本文针对智能网联车辆,结合车辆跟驰行为存在的延时性和传递性,引入紧邻多前车的最优速度和加速度改进OVCM模型,提出一种基于多前车最优速度与加速度(Multiple Optimal Velocities & Accelerations,MOVA)的网联车跟驰模型。
为了检验所提出模型在维持交通流稳定性方面的合理性,首先,利用线性稳定性分析计算MOVA模型的稳定性临界条件;然后,设定不同的加速度敏感系数和多前车数,分别描述车头距与最优速度敏感系数间的相位约束关系;最后,结合车辆速度和车头距等多项参数,对环形道路上的车队进行施加扰动后的数值模拟,并与OVCM等典型跟驰模型进行对比分析。
1 MOVA模型的建立
为了解决OVCM模型存在的间接解析前后车速度信息引发的延迟问题,以及更加准确地描述车辆跟驰行为特性,考虑引入紧邻多前车的最优速度记忆项和加速度项改进OVCM模型,得到改进模型的运动方程为:
[vnt+T=Vi=1kΔxn+i-1,Δxn-1,Δvn,i=1kan+i(t)] (1)
对式(1)进行展开描述,得到式(2):
[Vi=1kΔxn+i-1,Δxn-1,Δvn,i=1kan+i(t) =αVΔxnt+βTΔvnt+i=1kωikTan+i-1(t)+i=1kTγiVΔxn+i-1t-VΔxn+i-1t-τ] (2)
式中:[α]表示最优速度的敏感系数;[β]表示前后车速度差的敏感系数;[Δxnt]表示前后车车间距;[VΔxnt]表示跟驰车的最优速度函数;[T]为人为和机械因素产生的延时;[k]([k≥1])表示紧邻前车的数量(含跟驰车);[ωi]表示第[n+i-1]辆车加速度信息[an+i-1(t)]的敏感系数;[τ]表示采样时间间隔;[γi]是第[n+i-1]辆车的最优速度记忆项[VΔxn+i-1t-VΔxn+i-1t-τ]的敏感系数。
[VΔxnt]的计算方法如式(3)所示:
[VΔxnt=Vmax2tanhΔxnt-hc+tanhhc] (3)
式中:[Vmax]为车辆的最大速度;[hc]表示车辆间的安全距离。
由于式(2)的延迟时间[T]不利于公式解析与模型仿真,且考虑到加速度对车辆控制的直接性,对式(2)进行简化,简化过程如式(4)~式(10)所示:
[vnt+T=vnt+Tant] (4)
将式(4)代入式(2)得:
[ant=1TVi=1kΔxn+i-1,Δxn-1,Δvn,i=1kan+i-1(t)-vnt] (5)
取[α=1T],将式(2)代入式(5)得:
[dvntdt=αVΔxnt-vnt+ βΔvnt+i=1kωikTan+i-1(t)+ i=1kγiVΔxn+i-1t-Δxn+i-1t-τ] (6)
忽略变量[Δxnt-τ]泰勒展开式的非线性项计算,简化后的[Δxnt-τ]为:
[Δxnt-τ=Δxnt-τdΔvntdt=Δxnt-τΔvnt] (7)
同理,简化后的[VΔxnt-τ]如式(8)所示:
[VΔxnt-τ=VΔxnt-τΔvntVΔxnt] (8)
将式(7),式(8)代入式(6)得到简化的运动方程,如式(9)所示:
[dvntdt=αVΔxnt-vnt+βΔvnt+i=1kωikTan+i-1(t)+i=1kγiτVΔxn+i-1tΔvn+i-1t] (9)
2 线性稳定性分析
为了分析判定所提出模型的稳定性,采用Lyapunov第一方法并结合线性谐波微扰法[8]分析MOVA模型的稳定性临界条件。假设车队稳定状态时的车头距为[h],行驶速度为[V(h)],每辆车的初始位置为[x0nt=hn+V(h)t]。如果对第[n]辆车施加扰动[ynt=eikn+zt],则第[n]辆车经历扰动后的位置如式(10)所示:
[xn(t)=x0n(t)+yn(t)] (10)
对式(10)求二阶导数得:
[d2yn(t)dt2=dvn(t)dt] (11)
令[Δyn(t)=yn+1(t)-yn(t)],则车头距[h]定义如下:
[Δxn(t)=h+Δyn(t)] (12)
将式(11),式(12)代入式(9),得到与扰动相关的微分方程:
[d2yn(t)dt2=αVhΔynt-dyn(t)dt+q=1NγqτVΔxn+q-1(t)dΔyn+q-1(t)dt+βdΔyn(t)dt+q=1NωqN?d2yn+q-1(t)dt2] (13)
式中[Vh=dVΔxndΔxnΔxn=h]。
由于[ynt=eikn+zt],令[e(ikn+zt)=eM],将式(13)中[ynt]按傅里叶级数展开得:
[z2=αVh(eik-1)-z+βz(eik-1)+q=1NωqNeikq+q=1NγqτVhzeikq-eikq-1] (14)
将式(14)的参数[z]按[z=z1ik+z2ik2]展开,得到[z1]和[z2]的表達式:
[z1=Vh z2=12Vh+1αβz1-1-q=1NωqNe(q-1)z21+q=1Nγqτe(q-1)z1] (15)
若[z2<0],则车队运行状态不稳定;反之,车队运行状态稳定[9]。根据式(15)中[z2]的表达式可进一步求出敏感系数[α]的取值范围[10],如式(16)所示:
[α>-βVh+1-q=1NωqNe(1-q)Vh2-q=1Nγqτe(1-q)VhVh] (16)
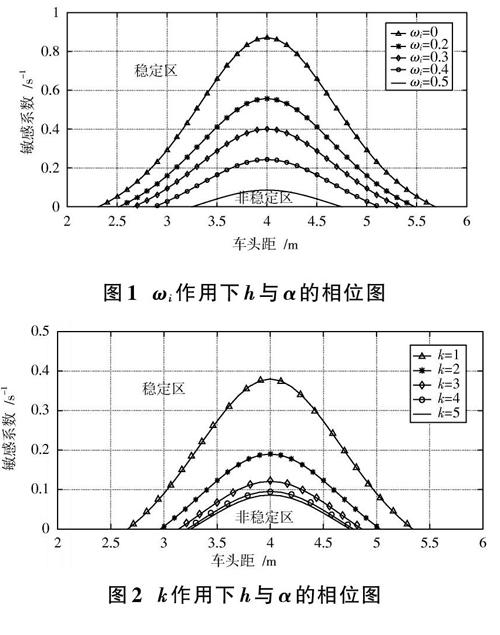
将最优速度记忆项敏感系数[γi]按照距离当前车由近到远的次序分别定义为0.1,0.08,0.06,0.04和0.02,取前车数[k=5],则不同[ωi]作用下车头距[h]与最优速度敏感系数[α]的相位图如图1所示;取加速度敏感系数[ωi=0.5],则不同[k]作用下车头距[h]与最优速度敏感系数[α]的相位图如图2所示。
图1和图2中曲线均表示稳定性临界曲线,即曲线以上部分为稳定区,以下部分为非稳定区。如图1所示,[ωi>0]时跟驰模型的稳定区域面积大于[ωi=0]时的跟驰模型,且[ωi]的增加有利于扩大稳定区域面积;同理,根据图2可得,[k>1]时跟驰模型的稳定区域面积大于[k=1]时的跟驰模型,且[k]的增加也能够将稳定区域面积逐渐扩大。由此可得,引入多前车最优速度记忆项和加速度项能够进一步维持交通流的稳定性。
3 数值模拟与分析
利用数值模拟验证所提出模型的有效性,将一列车队置于环形道路,测试条件及参数设置如下[6]:环形道路总长[L]取值为400 m,车辆数[N]取值为100辆,最大速度[Vmax]取值为2[m/s](即7.2 km/h),最优速度函数[11]为[V(Δxn(t))= 0.5Vmaxtanh(Δxn(t)-hc)+tanh(hc)]。安全车头距[hc]为4 m,最优速度敏感系数[α]为0.41 [s-1],前后车速度差敏感系数[β]为0.5 [s-1],最优速度记忆项敏感系数[γi]取值均为0.2 [s-1],采样时间间隔[τ]定义为0.2 s,延迟时间[T]定义为1 s。数值模拟过程中,位移表达式为[sn=sn-1+vn-1τ+0.5an-1τ2],速度表达式为[vn=vn-1+an-1τ]。
初始状态时,定义车队在环形道路的行驶速度为[V(LN)],所处位置[12][xn(0)=(n-1)LN],其中[n=1,2,…,N]。第1采样时刻,对第100辆车施加扰动后位置为[x100(1)=LN+0.2],观察施加扰动后整个车队的运行状态。
1) 数值模拟1:描述多前车加速度项对队列车辆速度波动幅度的影响
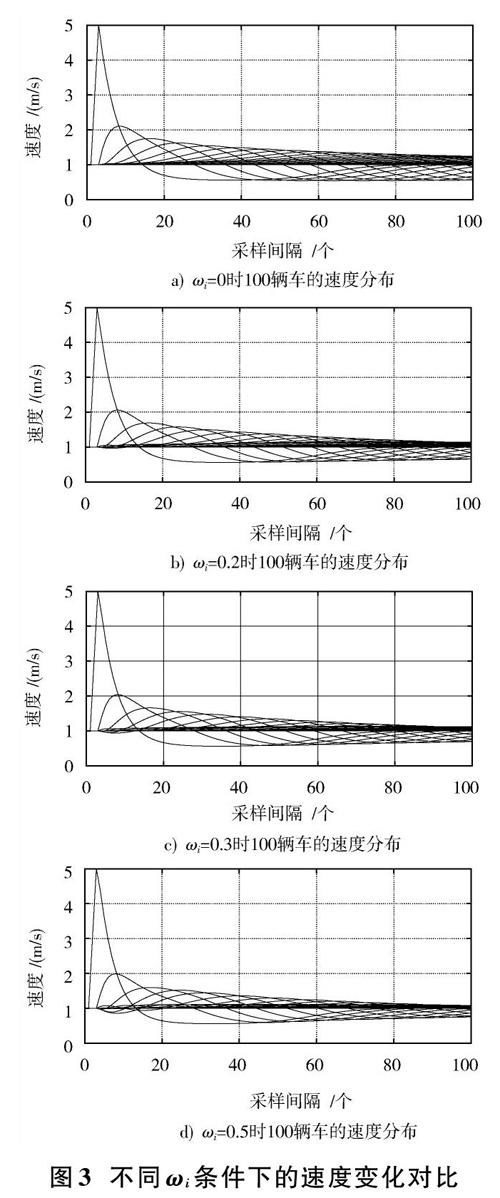
选定多前车数[k=4],采样间隔数为100个,车队所有车辆的速度变化曲线如图3所示。
分析图3可以得出,对第100辆车加入扰动后,其速度波动幅度迅速达到最大,随着仿真时间的推移,后续车辆的速度逐渐出现波动,且距离施加扰动车辆越远,其速度波动幅度越小。[ωi=0]时,车队的速度波动幅度大于[ωi≠0]时的情形,且随着[ωi]的增大(0~0.5),车队的速度波动幅度逐渐减小;但是,[ωi=0.3]时,在采样时刻0~20之间的速度波动幅度小于[ωi=0.5]时的情形,故后续数值模拟过程[ωi]的取值均为0.3。
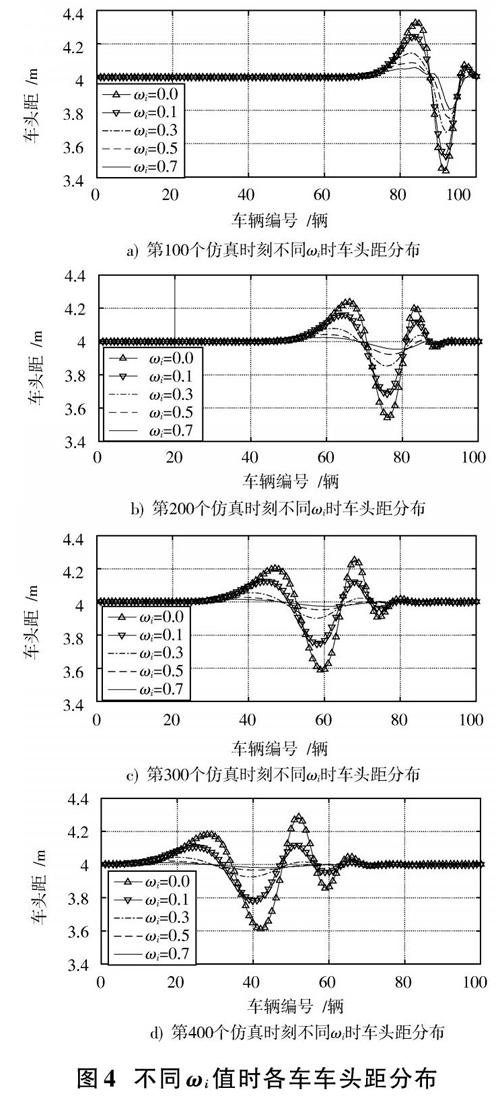
为了进一步验证引入多前车加速度项的影响作用,设定[ωi]取值集合为[0,0.1,0.3,0.5,0.7],定义前车数[k=5],分别观察100辆车在第100,200,300,400个采样时刻的车头距分布情况,具体分布结果如图4所示。
由图4可得:第100个采样时刻,扰动主要发生在第100辆车~第80辆车;第200个采样时刻,扰动主要发生在第90辆车~第60辆车;第400个采样时刻,扰动主要发生在第60辆车~第20辆车。同时,第100辆车加入扰动后,4个采样时刻的车头距波动变化存在相似性,即[ωi=0]时的车头距波动幅度明显大于[ωi≠0]时的情形,且随着[ωi]的增大车头距波动幅度逐渐减小。
综合图3与图4的测试结果,第100辆车的扰动对整个车队的扰动影响具有延时性和传递性,这两种特性的存在验证了引入多前车加速度项的合理性和必要性,且测试结果表明,引入多前车加速度项能够较好地稳定车速和车头距变化幅度,有利于促进车队的平稳运行。
2) 数值模拟2:描述多前车数[k]对队列车辆速度波动幅度的影响
设定多前车加速度项敏感系数[ωi=0.3]([i=1,2,…,k]),采样间隔数为500个;对第100辆车施加扰动后,在仿真前期队列中第100辆~第51辆车的扰动明显大于第50辆~第1辆车,故选择观察第90,80,70和60辆车的速度变化,测试结果如图5所示。
由图5可得,不同[k]值作用下,4辆观察车对应车头距波动变化也存在相似性,前车数[k=4]时的车速波动幅度明显低于[k=1]时的情形;前车数[k=6]时的車速波动幅度反而大于前车数[k=4]时的情形。由此可得,引入多前车信息([k>1])有利于控制队列车速波动幅度,但是[k]的取值不宜过大,主要原因在于:距离跟驰车较远的前车对跟驰车行驶状态的影响逐渐减弱,[k]取值过大反而引入多余的干扰信息,从而不利于车队稳定行驶。
3) 数值模拟3:对比OVCM等典型模型,验证引入多前车加速度项与最优速度记忆项对车队行驶稳定性的影响
设定多前车加速度项敏感系数[ωi=0.3],前车数[k]取值为4。不考虑紧邻前车加速度的影响,利用4辆前车信息对OVCM模型进行改进,可得到MHOV(Multiple Headway Optimal Velocity)模型。表1~表3描述了FVD,OVCM,MHOV和MOVA四种模型分别在第100,300和500个采样时刻的车辆速度分布情况。参数[Vmax],[Vave],[Vmin],[Rup],[Rdn]和[Rave]分别表示最大速度、平均速度、最小速度、向上波动率、向下波动率和平均波动率。
分析表1~表3可得:FVD模型和OVCM模型随着仿真时间的变化速度平均波动率逐渐增大,说明在前500个采样间隔内,两个模型的扰动没有得到有效控制,反之,MHOV模型和MOVA模型的速度平均波动率逐渐减小。同时,MOVA模型的速度平均波动率小于MHOV模型,说明本文提出的MOVA模型在扰动吸收的控制效果和响应时间方面具备较好的优越性。
4 结 语
为了更好地控制车队扰动引发的速度波动幅度,本文提出了一种基于MOVA的网联车辆跟驰模型。线性稳定性分析表明,引入加速度敏感系数[ωi]和前车数[k]有利于增大稳定区域面积。数值模拟结果表明,队列扰动存在延时性和传递性,引入多前车信息具备合理性和必要性;考虑多前车加速度项能够有效地控制队列速度与车头距波动幅度;设定合理的前车数[k],能够使MOVA模型对速度波动幅度达到更好的控制效果;MOVA模型相比FVD,OVCM和MHOV模型,其速度平均波动率随采样时间的增加呈逐渐减小趋势并达到最小值,证明该模型在促进车队行驶稳定性方面具有更好的优越性。由于数值模拟过程和模型参数设置的局限性,下一步考虑采用实际车辆队列数据修正MOVA模型的参数,以进一步增强MOVA模型对实际交通现象的模拟能力。
参考文献
[1] MIKA P. Adaptive car?following model [J]. Journal of mechanical engineering, 2018, 68(3): 281?288.
[2] 魏福禄,刘杨.经典跟驰模型的发展综述[J].吉林建筑大学学报,2018,35(4):19?23.
[3] AGHABAYK K, SARVI M, YOUNG W. A state?of?the?art review of car?following models with particular considerations of heavy vehicles [J]. Transport reviews, 2015, 35(1): 82?105.
[4] ZENG Y, ZHANG N. Review and new insights of the car?following model for road vehicle traffic flow [C]// 6th International Asia Conference on Industrial Engineering and Management Innovation (IEMI). Paris: Atlantis Press, 2016: 87?96.
[5] YU S, TANG J, XIN Q. Relative velocity difference model for the car?following theory [J]. Nonlinear dynamics, 2018, 91(3): 1415?1428.
[6] PENG G, LU W, HE H, et al. Nonlinear analysis of a new car?following model accounting for the optimal velocity changes with memory [J]. Communications in nonlinear science & numerical simulation, 2016, 40:197?205.
[7] 赵祥模,惠飞,史昕,等.泛在交通信息服务系统的概念、架构与关键技术[J].交通运输工程学报,2014(4):105?115.
[8] YU S W, SHI Z K. An improved car?following model consi?dering relative velocity fluctuation [J]. Communications in nonli?near science & numerical simulation, 2016, 36: 319?326.
[9] NGODUY D. Linear stability of a generalized multi?anticipative car following model with time delays [J]. Communications in nonlinear science and numerical simulation, 2015, 22(1/3): 420?426.
[10] 秦严严,王昊,冉斌.考虑多前车反馈的智能网联车辆跟驰模型[J].交通运输系统工程与信息,2018,18(3):48?54.
[11] 李腾龙.网联车环境下跟驰行为建模及交通流稳定性分析[D].西安:长安大学,2017.
[12] ZHU W X, ZHANG L D. A new car?following model for autonomous vehicles flow with mean expected velocity field [J]. Physica A: statistical mechanics and its applications, 2018, 492: 2154?2165.
