基于粒子群算法优化神经网络的电子音乐分类模型

2020-06-19张晓娜赵晶晶

现代电子技术 2020年9期

张晓娜赵晶晶

摘要：针对基于神经网络算法构建的电子音乐分类模型容易陷入局部最小值问题，分类精准度低，提出基于粒子群算法优化神经网络的电子音乐分类模型。构建模型时需先收集多种类型原生态电子音乐数据，去噪处理收集到的电子音乐数据，分帧和端点检测去噪后的电子音乐，从检测到的有效电子音乐信号中提取电子音乐的时域、频域方差特征和短时能量特征，采用灰色关联分析方法确定三种特征对电子音乐分类的贡献，加权操作上述特征，将加权后的三种特征作为粒子群算法优化的神经网络输入部分，通过优化后的神经网络输出电子音乐分类结果。经过实验分析发现，该电子音乐分类模型对10种电子音乐类型的分类结果与实际电子音乐所属类别相同，分类精准度较高。

关键词：电子音乐分类模型; 神经网络优化; 数据收集; 特征提取; 多特征融合; 分类结果输出

中图分类号： TN711?34 文献标识码： A 文章编号： 1004?373X（2020）09?0101?04

An electronic music classification model based on neural network

optimized by particle swarm optimization

ZHANG Xiaona， ZHAO Jingjing

（Shijiazhuang University， Shijiazhuang 050035， China）

Abstract： As the electronic music classification model based on neural network algorithm is prone to occurring of local minimum value and its classification precision is low， the electronic music classification model based on neural network optimized by particle swarm optimization is proposed. For the construction of the model， a variety of types of original electronic music data should be collected firstly， and then， the collected electronic music data are subjected to the denoising processing. After that， the denoised electronic music is subjected to the framing and endpoint detection. The time domain variance feature， frequency domain variance feature and short?time energy feature are extracted from the detected valid electronic music signal. The grey relational analysis （GRA） is used to confirm the contribution of the three features to the electronic music classification. Then the above three features are weighted. The weighted features are taken as the neural network input part optimized by particle swarm optimization， and the classification results of the electronic music are output by the optimized neural network. It is found in experimental analysis that， as for the ten types of electronic music， the electronic music classification result got by the proposed model is corresponding to the actual category of the electronic music. Therefore， the proposed model is of high classification precision.

Keywords： electronic music classification model; neural network optimization; data collection; feature extraction; multi?feature fusion; classification result output

0 引言

随着经济技术和科技的不断发展，人们和音乐之间的联系越来越紧密，音乐市场中出现多种电子音乐[1]。电子音乐可以降低人们生活和工作上的压力，由于不同用户对电子音乐的类型偏好不同，如何从大量电子音乐库中快速精准地找到用户所需电子音乐较为重要[2]。提高电子音乐查询效率的关键技术是电子音乐分类，因此，应重点研究如何建立一种分类性能较好的电子音乐分类模型[3]。

为建立分类性能较好的电子音乐分类模型，需分析当下电子音乐分类模型存在的缺陷，经过调查分析发现，当下最优电子音乐分类模型是基于神经网络的电子音乐分类模型。但是随着电子音乐数据的不断增加，基于神经网络构建的电子音乐分类模型出现分类效率低下、误分率较高以及容易陷入局部最小值的问题[4]，因此，应优化神经网络结构，建立一种基于粒子群算法优化神经网络的电子音乐分类模型，加快神经网络寻优能力[5]，提升电子音乐分类效果和分类精度。基于粒子群算法优化神经网络的电子音乐分类模型需提取电子音乐特征，通过提取的电子音乐特征描述电子音乐信息[6]，有效辨识电子音乐类型。

单一电子音乐特征能提供的电子音乐信息较少，无法精准描述电子音乐具体内容，不能实现电子音乐的正确分类[7]。电子音乐特征具有短时能量特征、时域特征和频域特征等较多特征，通过电子音乐特征可描述电子音乐详细的内容，因此，本文构建的基于粒子群算法优化神经网络的电子音乐分类模型中融合了多种电子音乐特征，实现了电子音乐的精准分类。

1 构建电子音乐分类模型

1.1 基本框架

基于粒子群算法优化神经网络的电子音乐分类步骤为：

1）从电子音乐中提取不同类型的音乐特征;

2）处理提取后的多个音乐特征，处理过程中采用灰色关联分析方法运算每个电子音乐特征的贡献率，用贡献率表示电子音乐特征对电子音乐分类的重要程度[8];

3）通过粒子群算法优化神经网络，获取最佳神经网络。通过该网络获取电子音乐分类结果。

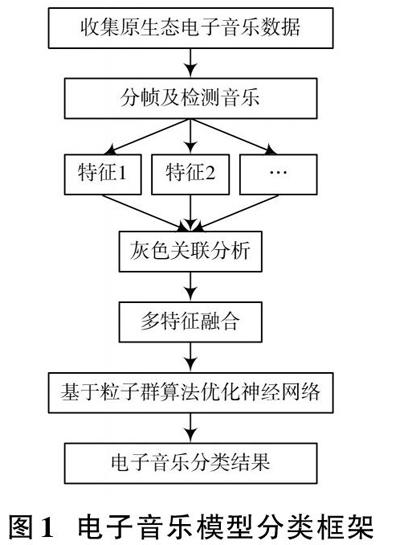
电子音乐分类模型的基本框架如图1所示。

从图1中可以看出，构建电子音乐分类模型时，应先收集多种类型的原生态电子音乐数据，去噪处理收集到的电子音乐数据。分帧和端点检测去噪后的电子音乐，获取有效的电子音乐信号[9]。从有效的电子音乐信号中提取电子音乐的时域、频域方差特征和能量特征，组合提取特征形成特征向量。采用灰色关联分析方法确定三种特征对电子音乐分类的贡献，加权操作上述特征，融合多种特征[10]。将加权后的三种特征作为基于粒子群算法优化后的神经网络输入部分，通过基于粒子群算法优化后的神经网络输出电子音乐分类结果。

1.2 音乐的多特征融合

1.2.1 提取音乐特征

针对电子音乐特征的多样性，构建电子音乐分类模型时需提取短时能量特征、时域方差特征等多种电子音乐特征，具体提取过程如下：

1）电子音乐短时能量特征。普通声音能量和电子音乐能量之间具有较大区别，与普通声音相比，电子音乐具有更高的能量值[11]，由此，可提取每一帧电子音乐短时能量特征。假设[Em]表示电子音乐信号[y（m）]的能量，则电子音乐信号[y（m）]的短时能量计算公式如下：

[Em=-∞+∞y（n）?c（n-m）2] （1）

式中[c（m）]表示窗函数。如果电子音乐信号帧的长度是[N]，那么此时[Em]的计算公式为：

[Em=n=0N-1y（n）?c（n-m）2] （2）

2）电子音乐时域方差特征。可通过式（3）描述电子音乐的某帧：

[Yt（n）=yt（n，1），yt（n，2），…，yt（n，N）] （3）

式中[Yt（n）]表示电子音乐的某帧，采用小波变换平滑操作[Yt（n）]后，获取处理后的电子音乐某帧为[Yt（n）]，此时，可通过式（4）描述处理后电子音乐的某帧，具体描述如下：

[Yt（n）=yt（n，1），yt（n，2），…，yt（n，N）] （4）

结合式（4），计算电子音乐时域的均值[Et（n）]和方差[Dt（n）]，均值和方差的计算公式如下：

[Et（n）=1Ni=1Nyt（n，i）] （5）

[Dt（n）=1Ni=1Nyt（n，i）-Et（n）2] （6）

3）电子音乐的频域方差特征。通过傅里叶变换电子音乐的某帧[Yi（n）]，变换后得到[Yf（n）]，变换后电子音乐的某帧描述过程如下：

[Yf（n）=yf（n，1），yf（n，2），…，yf（n，N）] （7）

采用小波变换平滑操作[Yf（n）=1Ni=1n（yf（n，i）-Ef（n））2]，得到[Yf（n）]，[Yf（n）]的表达式如下：

[Yf（n）=yf（n，1），yf（n，2），…，yf（n，N）] （8）

結合式（8）计算得到电子音乐的频域均值[Ef（n）]和频域方差[Df（n）]，具体计算公式如下：

[Ef（n）=1Ni=1Nyf（n，i）] （9）

[Df（n）=1Ni=1Nyf（n，i）-Ef（n）2] （10）

1.2.2 电子音乐特征具体融合

1）假设[Yi=（yi（1），yi（2），…，yi（m））]表示电子音乐短时能量特征、时域方差特征和频域方差特征构成的特征向量，表达式中[i=1，2，…，m]。

2）预处理[Yi=（yi（1），yi（2），…，yi（m））]，将参考对象设置为随机选择的一组特征向量，选取的特征向量为[Y′0=（y′0（1），y′0（2），…，y′0（m））]，选取的特征向量和其他组特征向量能构成特征向量对。

3）采用[Δi（k）=y′0（k）-y′i（k）]计算特征向量组最大偏差和最小偏差，最大偏差和最小偏差详细计算过程如下：

[P1=maximaxkΔi（k）P2=miniminkΔi（k）] （11）

4）计算电子音乐特征灰色关联系数，计算公式为：

[gi（k）=n+αMΔi（k）+αM] （12）

式中[α]表示分辨系数。

计算电子音乐特征的灰色关联度：

[gi=k=1nwigi（k）] （13）

式中[wi]表示权重。根据式（13）可获取电子音乐特征的贡献值，通过贡献值描述电子音乐中每种特征对电子音乐的影响程度[12]。

1.3 基于粒子群算法优化神经网络

采用粒子群算法优化神经网络，获取最优神经网络结构，通过最优神经网络结构得到分类结果。采用粒子群算法优化神经网络时，应先分析粒子群算法原理，依照粒子群算法原理优化神经网络结构，下面详细描述粒子群算法原理和粒子群算法优化神经网络的过程。

1.3.1 粒子群优化算法原理

标准粒子群算法的数学描述过程如下：假设搜索空间是[L]维空间，群体中总共含有[K]個粒子，第[j]个粒子的位置表示为[Xj=（xj1，xj2，…，xjl）]，第[j]个粒子的位置对应的最优解是[Pj=（pj1，pj2，…，pjl）]，[py]表示全局最优个体，第[j]个粒子的位置速度表示为向量[Vj=（vj1，vj2，…，vjl）]，根据下述公式迭代变化每个粒子的位置和速度：

[vjl（t+1）=g?vjl（t）+z1?rd（）?（pjl（t）-xjl（t））+z2?rd（）?（py（t）-xjl（t））] （14）

[xjl（t+1）=xjl（t）+vjl（t+1）] （15）

式中：[g]表示惯性因子;[z1]和[z2]表示加速因子，且加速因子为正常数;[rd（）]表示[0，1]之间的随机数值;[t]表示当前迭代代数。由于粒子群的速度和初始位置随机产生，可通过式（14）和式（15）迭代粒子位置和速度，直到满足终止条件时停止迭代。式（14）中惯性权重计算公式如下：

[g=gmax-（gmax-gmin）（s-save）smax-save， s≥savegmax， s

式中：[s]表示粒子适配值;[save]和[smax]分别表示每代粒子平均适配值和粒子群中最大适配值。

1.3.2 粒子群算法优化神经网络的步骤

依照上述分析的粒子群算法原理优化神经网络结构，通过粒子群算法训练神经网络权值和阈值，得到最优的权值和阈值[13]。根据最优权值和阈值构建最优神经网络结构，优化过程如下：

1）先归一化处理训练样本和测试样本，建立三层神经网络拓扑结构，将1.2节获取的加权后三种特征向量对的维数[M]作为神经网络输入层节点数[SI]，电子音乐类别数[LB]作为神经网络输出层节点数[CD]，输入层节点数和输出层节点数的几何均值为隐含节点数[YH]，种群中个体粒子表示为实数向量，实数向量是通过编码神经元之间所有阈值和连接权值获取的。此时，粒子群中每个粒子的维度[L]可表示为：

[L=（SI?YH）+（YH?CD）+YH+CD] （17）

2）设计适应度函数。评价神经网络解决问题能力的指标是适应度函数，采用神经网络输出值均方差获取目标函数，将目标函数的倒数作为适应度函数[14]，神经网络输出值均方差越小，说明对应粒子自身性能越好。目标函数计算公式为：

[MB=1upi=1uj=1p（bij-rij）] （18）

式中：[u]表示输出节点个数;[p]表示训练样本数;[bij]表示网络期望输出值;[rij]表示网络实际输出值。

3）初始化和设置参数。设置参数包括粒子个数、初始位置和速度，将初始位置和速度控制在[0，1]之间，同时设置加速因子、最大迭代次数等。

4）通过输入和输出的样本，依照式（18）计算种群中每个个体粒子适应度函数值，将历史最佳位置当成每个粒子的最好位置，开始迭代粒子。

5）采用粒子群算法中的式（14）～式（16）更新粒子的速度和位置。

6）检测粒子位置和速度是否在界限以内，如果粒子出现越界的状况，需排除越界粒子，重新更新粒子的速度和位置。

7）计算更新后粒子的适应度值，依照适应度值改变惯性权重，搜索粒子最佳位置。

8）检验是否符合结束标准。假设粒子当前位置与预定用的误差要求相符合时，停止迭代粒子，将神经网络的最终权值和和阈值输出[15]。假设粒子当前位置与预定用的误差要求相差较大时，需重新执行步骤4），直到满足条件为止。通过获取的权值和阈值构建最优神经网络，通过该网络输出电子音乐分类结果。

2 仿真实验

采用某电子音乐平台作为实验平台，实验中包含合奏乐、管弦乐、丝竹乐等10种电子音乐类型，实验结果如下所示。

2.1 分类结果

为验证本文模型的分类结果，选取我国联合电子音乐平台中的10种电子音乐作为训练样本，输入所选电子音乐特征，其中，用电子音乐音高、音长表示电子音乐频域特征，用混响时间和音调表示电子音乐时域特征，电子音乐短时能量均方根表示电子音乐能量特征，采用本文电子音乐分类模型分别输出10种电子音乐所属的电子音乐类型，实验结果如表1所示。从表1中可以看出，采用本文电子音乐分类模型能够有效分类10种电子音乐的类型，对比分类结果与电子音乐实际所属类别发现，本文电子音乐分类模型分类效果与实际电子音乐所属类别相同，说明本文电子音乐分类模型分类精准度较高。

2.2 分类效果

为验证本文电子音乐分类效果，实验从联合电子音乐平台用户中随机选取100名用户，让用户从10种电子音乐中选择自身感兴趣音乐。经过调查统计发现喜欢合奏乐的人较多，其次是丝竹乐和琴乐，其他音乐类型人数相对较少，对比本文分类效果和神经网络分类效果，对比结果如图2所示。从图2中可以看出，采用本文电子音乐分类模型分类电子音乐后，合奏乐占总电子音乐的21%，丝竹乐和琴乐分别占总电子音乐的18%和13%，与选取100名用户兴趣爱好相同，而传统神经网络分类模型分类后合奏乐占总电子音乐的5%，丝竹乐和琴乐分别占总电子音乐的5%和6%，与选取100名用户的兴趣爱好间存在一定偏差。综上所述，本文电子音乐分类模型分类效果较好。

3 结语

为提升电子音乐的分类精准率，本文提出基于粒子群算法优化神经网络的电子音乐分类模型。采用粒子群优化神经网络结构，依照粒子群训练神经网络的权值和阈值构建优化后的神经网络，将加权后的三种特征作为优化神经网络的输入，网络输出结果则为电子音乐分类结果。经过实验分析发现，本文电子音乐分类模型在采用粒子群优化神经网络实现分類的过程中，充分考虑了电子音乐的时域、频域方差特征和短时能量特征，对绣球、炎黄风情等10种电子音乐的分类精准度较高。

参考文献

[1] 赵宏伟，李圣普.基于粒子群算法和RBF神经网络的云计算资源调度方法研究[J].计算机科学，2016，43（3）：113?117.

[2] 王宗杰，邢明峰，王洪泊.基于粒子群优化BP神经网络的医患关系风险预警模型[J].北京工业大学学报，2017，43（1）：8?12.

[3] 徐大明，周超，孙传恒，等.基于粒子群优化BP神经网络的水产养殖水温及pH预测模型[J].渔业现代化，2016，43（1）：24?29.

[4] 闫滨，王闯.基于粒子群优化算法的RBF神经网络在闸墩裂缝宽度预测中的应用[J].水力发电，2018，44（3）：33?36.

[5] 程军，李荣钧.基于粒子群优化的神经网络预测模型[J].数学的实践与认识，2015，45（3）：176?180.

[6] 张键锋，王劲.基于文本挖掘与神经网络的音乐风格分类建模方法[J].电信科学，2015，31（7）：80?85.

[7] 肖晓红，张懿，刘冬生，等.基于隐马尔可夫模型的音乐分类[J].计算机工程与应用，2017，53（16）：138?143.

[8] 杜威，林浒，孙建伟，等.一种基于分层结构的音乐自动分类方法[J].小型微型计算机系统，2018，39（5）：888?892.

[9] 邵曦，姚磊.基于SVM主动学习的音乐分类[J].计算机工程与应用，2016，52（6）：127?133.

[10] 金梅，张伟亚，张淑清，等.基于改进PSO和DE优化神经网络的电能质量扰动分类[J].高技术通讯，2018，28（4）：291?298.

[11] 杨晓宇，黄浩，王浩华.基于改进的T型关联度在音乐分类中的应用[J].数学的实践与认识，2017，47（20）：157?165.