基于投资者结构的P2P网贷项目评估模型研究

杨希　范雯娟　杨善林

摘 要：从投资者行为角度出发，以社会学橄榄型社会理论为理论框架架构了针对中国市场的P2P网贷项目投资者结构评估模型。模型通过求解衡量目标项目投资者结构指标与标准指标之间的离散程度进而判断其投资者结构的优劣。实证研究表明模型可有效评估P2P网贷项目的投资价值，为投资者决策提供参考。

关键词：P2P网贷项目;投资者行为;投资者结构;橄榄型社会理论

中图分类号：F832.48

文献标识码：A文章编号：

1672-1101（2020）02-0042-07

收稿日期：2019-10-25

作者简介：杨希（1989-），男，安徽淮南人，在读博士，研究方向：管理科学与工程。

Research on evaluation model of P2P loan project based on investor structure

YANGXi，FANWenjuan，YANGShanlin

（School of Management， Hefei University of Technology， Hefei230009， China）

Abstract： From the perspective of investor behavior， the investor structure evaluation model for P2P online loan project for the Chinese market is constructed with the sociological olive-type social theory as the theoretical framework. The model determines the advantages and disadvantages of the investor structure by solving the degree of dispersion between the index and the standard index of the target project. The empirical evidence shows that the model can effectively evaluate the investment value of P2P net loan project and provide reference for investors' decision-making.

Key words：P2P online loan project; Investor behavior; Investor structure; Olive-shaped social theory

一、文獻综述

P2P网络借贷凭借其较低的投资门槛和较高的预期年化利率等特点在全球金融科技领域内占有重要地位，成为大众投资的一个重要渠道。因而研究投资者行为对金融市场影响的已有成果很多。宏观上，从全球金融市场到区域金融市场，不同层面都有研究。如Peihua Fu等的研究表明投资者社会网络的传播率和非均质结构是对庞氏骗局的财务结果产生积极影响的两个关键因素，而成本和费用的比率则是对其产生负面影响的另一个因素[1]。B. Tóth等发现金融市场参与者之间的相互行为具有以下特点：一是投资者在流动性供应方面的差异很大;二是其他投资者的行为会对投资者的投资决策产生更为强烈的影响;三是市场指令的总体影响是投资者在不同方向上分别推动价格和流动性的微妙补偿的结果，这一结果导致了异质参与者之间竞争的市场现状，其相互间的作用形成了一个复杂的市场生态[2]。

微观上，不少学者从投资者行为对具体金融产品的影响角度出发分析相关问题。如Castellano， R等总结了投资者的特点：一是金融知识或金融产品的模糊框架会导致散户投资者对全球趋势类型的误解，从而导致无法盈利决策;二是在散户投资者中，一些复杂的结构性产品比简单的结构性产品更受欢迎;三是在结构性产品的特殊情况下，散户投资者的行为是由对提供投资刺激的金融机构的信心所驱动的[3]。Niehaus， G等发现，在投资组合中投资者不愿意出售表现不佳的资产，倾向于出售表现良好的资产，这种行为在很多情况下并不是最优的投资决策[4]。

从现有研究成果不难看出，绝大部分的研究标的都是传统金融产品，而P2P网贷项目在产品属性上和传统的金融产品有着显著的差异，故很多金融学领域内的研究思路并不适用于分析这类产品。本文尝试从行为金融学角度入手，以社会学橄榄型社会概念为理论框架，通过分析中国P2P网贷市场发展行情建立具体的投资结构分析模型，并根据模型对投资项目进行评估形成量化指标，为投资者提供理论参考。

二、理论框架

橄榄型社会最先由著名经济学家赵海均先生提出。2010年温家宝总理在《求是》杂志发表文章指出，要逐步形成中等收入者占多数的“橄榄型”分配格局[5]，首次提出了建设橄榄型社会的目标，从此这一目标成为中国政府的一项长期政治政策。橄榄型社会结构是一种基于收入阶层的结构，从左到右依次为贫困阶级、中产阶级和富裕阶级。社会学理论认为，这种中产阶级占绝大多数的社会结构是最有利于社会发展的结构。

金融学和投资学中投资项目的投资者结构问题，对社会发展的作用类似于社会结构对社会发展的影响，因而分析投资者结果问题。社会学中社会结构是按照收入水平划分的，并且认为健康的社会结构会带来良好的发展潜力。这一点和P2P网贷项目中的投资者结构有着十分类似的地方，良好的投资者结构同样也可以反映P2P网贷项目的投资潜力。按照社会学对社会结构的划分依据，P2P网贷项目的投资者结构也可以根据投资金额的多少划分成为低额投资、中等投资和高额投资三个层次。由于投资者结构是由已经发生的投资行为产生的，所以其本质上反映了投资者在投资项目中的行为和意愿。当这种行为和意愿在市场中存在某种规律和联系时，掌握这种规律和联系就可以为投资者在市场中的投资决策提供指导。

在对P2P网贷项目的投资者结构进行研究时，必须深刻理解项目的自身特点和所处的市场环境带来的影响。由于中国的P2P网贷市场发展的还不成熟，投资者对于该领域的了解也不够深入，因而大批投资者在投资时为了降低风险选择了分散投资，这导致具体投资项目中处于低额投资水平的人数过多。由于投资者选择项目的原因并不是因为掌握了有效信息和分析方法，只是为了分散风险而已，故投资行为往往无法有效反映项目的投资价值。所以，尽管某项目低额投资阶层占总投资人数比例很高，也并不能说明项目具有较高的投资价值。

和低额投资阶层情况类似，高额投资阶层占总投资人数比例较高的投资者结构也不利于对项目的评估。首先，投资金额的高低是一个相对概念，如果投资项目中大部分投资者都投入了很高的资金，那么相对的中等投资阶层的划分标准也会被相应的提高。其次，如果项目的高额投资者過于集中，其带来的风险聚集度也会相应的升高。结合当前中国P2P网贷市场环境，极有可能出现网贷诈骗情况，因而是一种十分不健康的投资结构。

而当中等投资阶层占总投资人数比例较高时，对P2P网贷项目而言是非常健康的投资者结构。这部分投资者在进行投资时大都对项目具有一定的了解和研究，对项目的投资潜力有着相对客观的评估，且适度的投资力度也不会造成过高的风险聚集度，因而这类项目十分具有投资价值。

综上所述，社会学中的橄榄型社会理论适用于金融学中的投资者结构分析，P2P网贷项目理想的投资者结构是中间大两头小，而中等投资阶级的规模可以成为判断项目投资潜力的标准。

三、模型构建

（一）模型设计

P2P网贷项目的风险本质就是违约概率，不同项目虽然在违约概率上不尽相同，但体现在最终结果上就只有违约和不违约两种结果。故即使不同违约概率的产品最终的结果都是不违约，但在进行投资时，选择投资者结构最佳的项目，事实上已经在潜在违约事件发生之前最大限度的规避了风险，从而使得投资资金更有保障。概念化的橄榄型社会理论无法具体衡量投资者结构的好坏，故在建立具体的评估模型时我们需要将这种概念量化。

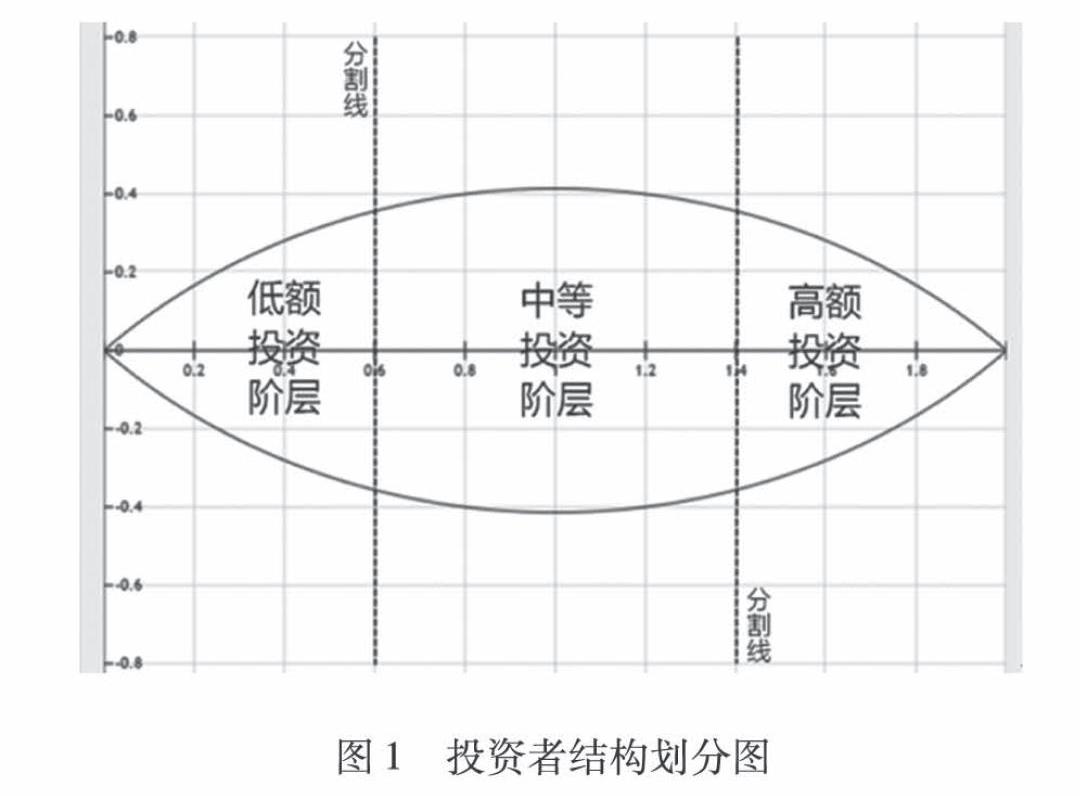
如图1所示，处于平面直角坐标系中的橄榄形结构，其整体面积代表了所有参与图形所代表的P2P网贷项目的投资者结构。通过两条垂直于X轴的直线将橄榄形分成了三个部分，这三部分图形面积所占橄榄形面积的比例和三类投资者阶层中的人数所占总投资者人数的比例相同，相对应的投资者阶层从左到右依次为低额投资阶层、中等投资阶层和高额投资阶层。当三类投资阶层在投资者结构中所占的比例发生变化时，橄榄形中相应区域的面积也会随之以相同的比例发生变化，而划分区域的两条分割线在直角坐标系中的位置也会随着划分区域面积的变化而在橄榄形的长轴上来回变化。三者之间的联系使得每一种投资者结构在橄榄形中都会有唯一的一组分割线在橄榄形长轴上与其对应，故可依据两条分割线在橄榄形长轴上的位置为指标对投资者结构建立相应的量化模型。

橄榄型社会结构本质上是一种中间大两头小的结构，当该结构中分割线在长轴上的位置发生改变时，在长轴上的不同位置移动单位距离对划分区域带来的面积上的变化是不相等的。分割线的位置越接近橄榄形的短轴，单位距离的变化带来的面积变化越大;分割线的位置越远离橄榄形的短轴，单位距离的变化带来的面积变化越小。我们把这种情况定义为分割线的灵敏度，区域中单位面积变化带来的分割线的移动距离越长，灵敏度越高;反之，灵敏度越低。

（二）投资者结构评估模型的建立

建立评估模型之前，我们首先要建立一个标准的橄榄形。

如图2所示，直角坐标系中面积相等的两个圆，圆心的坐标分别为（a，b）和（a，-b），两圆相交部分即是一个橄榄形。为方便计算面积，我们令a=1、b=1，就建立了一个面积为π-2的标准橄榄形，其函数表达式为：

x-12+y+12=2，y≥0

x-12+y-12=2，y≤0（1）

由于标准橄榄形被X轴分成了面积相等的上下两个部分，而分割线又是垂直于X轴的，故我们在计算分割区域的面积时，可以只计算分割区域中处于橄榄形上半部分的面积后再乘以2。将橄榄形上半部分的函数表达式转化成关于X的函数表达式，结果为：

f（x）=2-x-12-1，x∈0，2（2）

如图3所示，设两条垂直于X轴的分割线分别和X轴交于点A1和点A2两点，则两条分割线在长轴上的位置，就可以通过线段A1A2的长度和其在长轴上的位置来唯一确定，并最终成为衡量投资者结构的指标。设点A1坐标为（m，0），点A2坐标为（n，0），则两条分割线的函数表达式为y=m和y=n，分别求解f（x）在[0，m]、[m，n]和[n，2]上的定积分。则f（x）在区间[0，m]上积分的2倍与橄榄形面积的比重就是低额投资阶层在整个投资结构中所占的比例;f（x）在区间[m，n]上积分的2倍与橄榄形面积的比重就是中等投资阶层在整个投资结构中所占的比例;f（x）在区间[n，2]上积分的2倍与橄榄形面积的比重就是高额投资阶层在整个投资结构中所占的比例。设低额投资阶层占比为E1，中等投资阶层占比为E2，高额投资阶层占比为E3，其方程表达式为：

E1=2π-2∫m02-x-12-1dx

E2=2π-2∫nm2-x-12-1dx

E3=2π-2∫2n2-x-12-1dx（3）

当我们已知目标项目投资者结构的基本信息时，就可以通过带入相关数据计算出m和n的具体数值。将线段A1A2定义为指标线段，在已知m和n具体数值的情况下可以将指标线段的长度和其在长轴上的唯一位置确定，其中指标线段的位置可以由其中心点在长轴上的所在位置来定义。设指标线段的长度为l，中心点坐标为（c，0），则l和c的函数表达式为：

l=n-m

c=m+n2（4）

求得的指标线段的具体数值就代表了目标项目的投资者结构情况。将其和优良项目的投资者结构的指标线段进行对比，通过计算两者之间离散程度的大小可以判断目标项目投资者结构的好坏。两者之间的离散程度越低，目标项目的投资者结构就越好;两者之间的离散程度越高，目标项目的投资者结构就越坏。

如图4所示，两个目标项目的指标线段分别为B1B2和C1C2，其中B0为B1B2的中点，C0为C1C2的中点。以B0为端点做一条垂直于X轴的线段B0B3，使得线段B0B3的长度和线段B1B2的长度相等;在同一象限以C0为端点做一条垂直于X轴的线段C0C3，使得线段C0C3的长度和线段C1C2的长度相等。过点C3做一条垂直于线段B0B3的直线交B0B3于点D，形成了一个直角三角形△C3DB3。其中直角边DC3的长度即是两个项目指标线段间的相对距离，而直角边DB3的长度即是兩个项目指标线段长度的差值，故斜边B3C3的长度即可作为衡量两个目标项目指标线段间离散程度大小的标准。

设B0点坐标为（c1，0），C0点坐标为（c2，0），线段B1B2的长度为l1，线段C1C2的长度为l2，则指标线段B1B2和C1C2的离散值函数表达式为：

F=c2-c12+l1-l22（5）

通过这一模型，在已知最优投资者结构的指标线段时，就可以利用其对目标项目投资者结构的好坏进行量化和评估，也可以通过相互比较目标项目之间的离散值，排序投资价值，从而更好地辅助投资者进行投资决策。

四、实证分析

人人贷是中国P2P网贷行业中的代表平台，运营时间久，经营业绩优秀，风控水平过硬，综合实力更是长年位居中国P2P网贷行业前列，以其平台上的投资项目作为分析对象不但能够排除很多基于平台因素的不必要干扰，更重要的是对相关产品的评估具备更高的分析价值。

（一）平台投资者结构划分标准的定义

在对平台上的P2P网贷项目进行评估之前，必须要对其投资者结构的阶层分类标准进行定义。在和人人贷相关的数据当中，名为投资人数分级的指标可以反映出平台上不同投资水平的投资者人数。这一指标根据投资者在平台上的投资总额分出了四个档次，投资水平在0-1万元范围内的投资人数占总投资人数的70.48%;投资水平在1-10万元范围内的投资人数占总投资人数的25.87%;投资水平在10-100万元范围内的投资人数占总投资人数的3.57%;投资水平在100万元以上的投资人数占总投资人数的0.08%。指标划分的依据是投资者在平台上的总投资额，但投资者在平台上往往投资了不止一个项目，故这一标准不能直接用于具体项目投资者结构的划分中，但这并不意味着不能通过这一指标间接为项目投资者结构的标准进行量化。

虽然针对平台投资总额的投资者阶层划分标准并不适用于单一项目的投资者结构评估中，但同一投资者阶层在平台上的投资总额占平台总投资金额的比例，与该投资者阶层在具体项目中的投资总额占项目总投资金额的比例应该是一致的，我们可以根据这一点为P2P网贷项目建立具体的投资者阶层划分标准。

设平台的总投资人数为Z，将投资水平在0-1万元范围内的投资者的人均投资水平量化为0.5万元，并定义为低额投资阶层;将投资水平在1-10万元范围内的投资者的人均投资水平量化为5.5万元，并定义为中等投资阶层;将投资水平在10-100万元范围内的投资者的人均投资水平量化为55万元，而在投资水平超过100万元的投资者中，最高的投资金额达到了2 000多万元，且有相当一部分投资者的投资金额集中在1 000万元左右，故将其人均投资水平量化为1 000万元。将这两部分投资者定义为高额投资阶层。设低额投资阶层占总投资额的比例为G1，中等投资阶层占总投资额的比例为G2，高额投资阶层占总投资额的比例为G3，则G1、G2、G3的表达式分别为：

G1=0.5*0.7048*Z0.5*0.7048*Z+5.5*0.2587*Z+55*0.0357*Z+1000*0.0008*Z=0.0776

G2=5.5*0.2587*Z0.5*0.7048*Z+5.5*0.2587*Z+55*0.0357*Z+1000*0.0008*Z=0.3135

G3=55*0.0357*Z+1000*0.0008*Z0.5*0.7048*Z+5.5*0.2587*Z+55*0.0357*Z+1000*0.0008*Z=0.6089（6）

通过这些比例就可以求解出具体项目中三个阶层各自投资总额的大概数值，从而计算出划分投资阶层的具体标准。设参与项目的投资者人数为n，将投资者的投资金额按从低到高的顺序依次排列并设为s1、s2、s3… sp… sq … sn-2、sn-1、sn。令：

0.0776*∑ni=1si=∑pi=1si

0.6089*∑ni=1si=∑ni=qsi（7）

则sp对应的投资金额就是划分低额投资阶层和中等投资阶层的标准，而sq对应的投资金额就是划分中等投资阶层和高额投资阶层的标准。通过划分标准就可以求出P2P网贷项目中对应投资阶层的投资人数，从而得出项目的投资者结构。

（二）投资者结构的标准定义

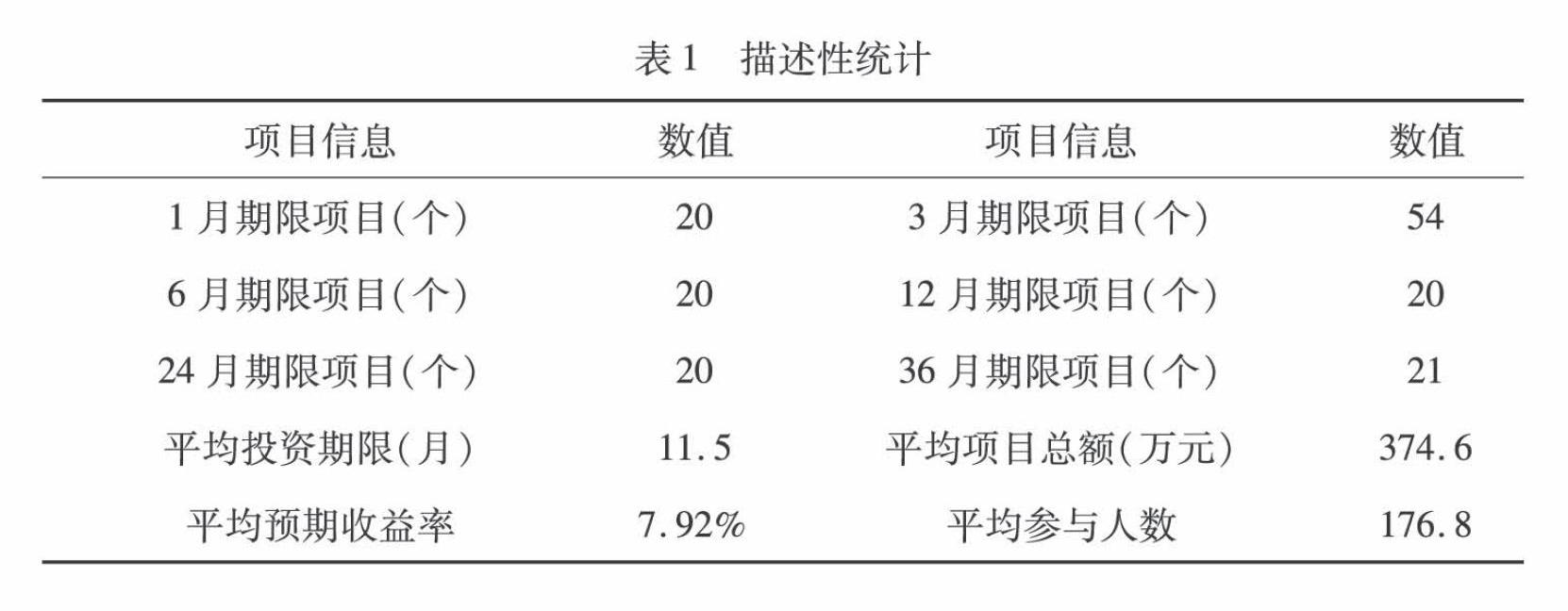
在求得目标项目的投资者结构之后，还需要将平台中公认的优质项目的投资者结构进行量化后作为标准，通过对比目标项目和标准项目在投资者结构上的离散程度，判断目标项目投资者结构的好坏。对于人人贷来说，U计划中的投资项目无疑是作为标准项目的最佳选择。本文选取了U计划中的155个投资项目作为研究对象，基本包含了平台中所有投资项目的类型，能够获取的项目信息包含项目总额、预期收益率、参与人数和投资期限，具体的描述性统计如表1所示。

按照步骤对这155个投资项目的投资者结构进行量化并求出其指标线段中l和c的值，再分别利用项目总额、预期收益率、参与人数和投资期限对l和c进行回归分析，结果如表2、表3所示。

从表2和表3可以得出，无论是关于l的回归结果还是关于c的回归结果，常数项和所有变量均显著。设预期收益率为v1，投资期限为v2，项目总额为v3，参与人数为v4，根据回归结果最终得出的关于l和c的方程为：

l=-0.854+25.87*v1-0.062*v2+0.002*v3-0.003*v4

c=1.245-3.359*v1+0.008*v2-0.001*v4（8）

根据以上两个方程，我们就可以求出任意目标项目的标准投资者结构的指标线段，再通过计算项目实际投资者结构与标准投资者结构间的离散程度，进而判断目标项目投资者结构的好坏。

（三）项目投资者结构的评估

为了让研究更具有代表性，本文特地从不同投资期限的投资项目中各随机抽取了1个项目共计6个项目，其项目信息如表4所示。

通过计算目标项目的投资者结构和标准投资者结构之间的离散程度，对其投资价值进行排序。计算结果如表5所示。

表5中参与评估的项目均按照离散值F的大小进行升序排列，目标项目的F值越小，其投资者结构就越好，投資价值也就越高。故5号项目是最佳投资对象;3号项目和1号项目基本属于同一档次，是仅次于5号项目的投资对象;6号项目和4号项目的情况稍差，投资之前需要对项目进行进一步的调研;2号项目情况最差，一般情况下不建议进行投资。基于这一指标所提供的项目信息，投资者就可以结合自身具体情况，灵活选择投资策略。

五、总结

本研究基于投资者行为角度，通过分析P2P网贷项目的投资者结构评估项目的投资价值。在对P2P网络借贷这一互联网金融产品的特点进行分析后，基于社会学橄榄型社会理论建立了具体的量化模型。通过这一模型将目标项目的投资者结构量化成为以指标线段为核心的指标，使得不同的项目之间可以通过对比指标线段之间的离散程度来判断投资者结构的优劣，并能够以此为标准对目标项目进行排序，方便投资者进行相关的投资决策。

在实证研究过程中，本文提出了一种划分P2P网贷平台投资者投资阶层的思路，依照这一思路订制了平台中项目投资者结构的划分标准。依据人人贷平台数据，选取了U计划中的优质项目投资者结构作为标准，并求解出了标准指标线段和项目信息的回归方程，通过这一方程，任何平台中的项目都可以利用项目信息计算出理想的投资者结构。之后随机选取了6个不同规格的P2P网贷项目，并通过计算其实际指标线段和标准指标线段之间的离散程度，对目标项目投资者结构的优劣情况进行了排序。研究结果显示，该方法让投资者对目标项目的投资者结构有了一个直观而具体的认识，并使得目标项目彼此间的比较成为了可能，对于投资决策十分具有参考价值。而社会学领域中橄榄型社会理论在金融领域的成功运用，也为针对此类金融产品的量化评估研究，提供了一种新的研究思路。

参考文献：

[1] Peihua Fu， Anding Zhu，He Ni， et al. Threshold behaviors of social dynamics and financial outcomes of Ponzi scheme diffusion in complex networks[J]. Physica A-Statistical Mechanics and Its Applications， 2018，15（1）： 632-642.

[2] B. Tóth，Z. Eisler，F. Lillo， et al. How does the market react to your order flow？[J].Quantitative Finance， 2012， 12（7）： 1 015-1 024.

[3] CastellanoR，R. Cerqueti.theory of misperception in a stochastic dominance framework and its application to structured financial products[J]. IMA Journal of Management Mathematics， 2018， 29（1）： 23-37.

[4] NiehausG，D.Shrider.Framing and the disposition effect：evidence from mutual fund investor redemption behaviour[J]. Quantitative Finance， 2014， 14（4）： 683-697.

[5] 温家宝. 关于发展社会事业和改善民生的几个问题[J]. 求是， 2010（7）：1-9.

[6] CheriyanV， A.J. Kleywegt.A dynamical systems model of price bubbles and cycles[J].Quantitative Finance， 2016， 16（2）： 309-336.

[7] HildebrandT， M.Puri， J. Rocholld. Adverse Incentives in Crowdfunding[J].Management Science， 2017， 63（3）： 587-608.

[8] ZakamoulineV.Portfolio performance evaluation with loss aversion[J].Quantitative Finance，2014，14（4）：699-710.

[9] HensT，M.O. Rieger. Can utility optimization explain the demand for structured investment products？[J]. Quantitative Finance， 2014， 14（4）： 673-681.

[10] Grishina N， C.A. Lucas， P. Date. Prospect theory-based portfolio optimization： an empirical study and analysis using intelligent algorithms[J].Quantitative Finance， 2017， 17（3）：353-367.

[11] Feldman T.Investor behaviour and contagion[J].Quantitative Finance，2014，14（4）： 725-735.

[12] Steve Y.Yang，Qifeng Qiao，Peter A.Beling， et al.Gaussian process-based algorithmic trading strategy identification[J].Quantitative Finance， 2015，15（10）： 1 683-1 703.

[13] Biondo， A.E. A. Pluchino， A. Rapisarda. Micro and macro benefits of random investments in financial markets[J].Contemporary Physics，2014， 55（4）： 318-334.

[责任编辑：吴晓红]