基于FPGA的有限域NTT算法设计与实现

谢星 孙玲 黄新明 韩赛飞

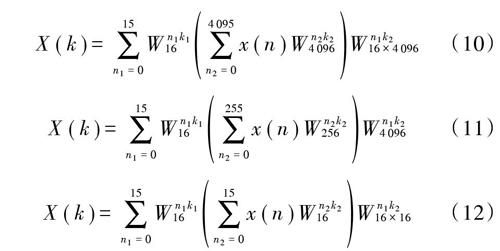
摘  要： 大数乘法是公钥加密系统中最为核心的模块，同时，也是RSA、全同态等加密方案里最耗时的模块，因此，快速实现大数乘法是急需解决的问题。64K点有限域NTT作为大数乘法器的关键组件，文中采用并行架构实现NTT的运算，运算中基本采用加法和移位操作，以保证实现大量的并行处理，提高了处理速度。该组件在Stratix?V FPGA上得到了实现，工作在123.78 MHz频率下，运行结果表明，在FPGA上的效率是CPU上运行速度的60倍。运行结果与GMP运算库进行比较，验证了有限域64K点NTT算法的正确性。

关键词： 有限域NTT算法; FPGA平台; 全同态加密; 大数乘法; 并行处理; 运行速度比较

中图分类号： TN915.08?34                        文献标识码： A                        文章编号： 1004?373X（2020）09?0079?04

Design and implementation of finite field NTT algorithm based on FPGA

XIE Xing1， 2， 3， SUN Ling3， HUANG Xinming3， HAN Saifei3

（1. Nantong University Xinglin College， Nantong 226019， China; 2. Engineering Training Center， Nantong University， Nantong 226019， China;

3. School of Electronic Information， Nantong University， Nantong 226019， China）

Abstract： The large number multiplication unit is the most important core module in the public key encryption system， and is the most time?consuming module in RSA and fully homomorphic encryption schemes. Therefore， it is urgent for researchers to realize fast large number multiplication. A 64K?point finite field NTT （number theoretical transform） is a key module of large number multiplier. A parallel architecture is adopted in this paper to realize the operation of the NTT. Basically， the addition and shifting operations are adopted in the operation to ensure the realization of a large number of parallel processing， which improves the processing speed. The module is implemented based on Stratix?V FPGA （field programmable gate array）. The operating results show when the working frequency of the module is at 123.78 MHz， its speed when running on FPGA is 60 times higher than the speed when running on CPU. The operation results were compared with that of the GMP arithmetic library， which verified the correctness of the 64K?point finite field NTT algorithm.

Keywords： finite field NTT algorithm; FPGA platform; fully homomorphic encryption; large number multiplication; parallel processing; operation speed comparison

0  引  言

云存储和云计算服务已然成为一种新兴的市场趋势，数据的私密性也成为人们享用云服务过程中关心的热点和难点问题[1]。现有技术中，即使用户对数据加密，也仍然需要向云端提供密钥才能进行运算或搜索等。同态加密方案允许云服务器在密文上直接进行任意的运算，即数据在加密状态下被处理，不会暴露原文信息[2]。然而，同态加密方案的算法复杂度极高，导致实际运行效率很低。因为在现有全同态加密（FHE）算法基础上，为了保证同态计算安全，密钥被做得非常大，即使对于小的安全设置尺寸2 048，每个源被加密到约750K位。随后所有的计算将直接对这些密文进行操作，都是大数的运算。

大数乘法是同态加密运算中的基本单元，广泛应用于其中的每一步。本文对大数乘法器中的关键组件64K点有限域NTT单元进行了设计与实现，最终运算结果与GMP运算库进行比较，验证了设计的正确性。本文首先简要分析了全同态加密方案以及大数乘法的特点;然后详细给出了64K点有限域NTT单元算法原理，提出了该单元的硬件设计架构，并完成了硬件设计，在FPGA上进行了功能仿真与验证，对仿真结果进行了验证。该高效有限域NTT模块还可以在其他密码学算法中广泛应用，下面给出64K点有限域NTT的具体分析设计过程。

1  全同态加密算法

全同态加密[R]和[S]是域，加密函数[E]：[R]→[S]，在使得[x]和[y]的信息不泄露的前提下，如果存在一种有效算法，使得[E（x+y）=E（x）⊕E（y）]或者[x+y=D（E（x）⊕E（y））]成立，则称函数[E]为加法同态;在使得[x]和[y]的信息不泄露的前提下，如果存在一种有效算法，使得[E（xy）=E（x）?E（y）]或者[xy=D（E（x）?E（y））]成立，则称函数[E]为乘法同态;如果函数[E]既是加法同态又是乘法同态，那称[E]为全同态加密。

Gentry?Halevi提出的基于整数的同态加密方案，包括密钥生成、加密、解密和重加密（Recryption）过程[3]。其中，密钥可以离线生成，所以相应模块不需要硬件设计。如式（1）所示，加密过程是用公共密钥[（d，r）]对原文进行多项式求值运算从而得到[c]密文，[b]是1 bit的原文数据。如式（2）所示，解密过程主要完成一个模乘运算，其中，[w]是私钥。在Gentry的实现中[4]，密钥一般为785 000 bit，正是因为密钥如此之大，导致同态加密方案的复杂度非常高。因为所有加密、解密以及重加密运算都是基于785 000 bit的模乘运算，所以快速的大数模乘运算成为该加密方案首要解决的关键问题。

[c=[u（r）]d=b+2i=1n-1uirid] （1）

[m=[c*w]dmod 2] （2）

式中[ui]为加密过程中随机生成的“噪声矢量”。

2  有限域快速数论变换NTT

通常来说，快速傅里叶变换（FFT）计算在复频域进行浮点运算被广泛应用于信号处理。但复域FFT的乘法运算需要舍入操作，计算量大，可能导致误差增大。此外，与定点运算进行比较，浮点运算消耗大量的硬件资源。离散傅里叶变换（DFT）公式如下：

[Xk=n=0N-1xne-2πiNnk，    0≤k≤N-1] （3）

离散傅里叶逆变换公式为：

[xn=1Nk=0N-1Xke2πiNnk，    0≤n≤N-1] （4）

在FFT中，通过[n]次单位复根进行运算，而对于NTT，则是将[rp-1N（mod p）]等价于[e-2πiN]，其中，[r]是模素数[p]的原根（由于[p]是素数，则原根一定存在），即：

[e-2πiN≡rp-1N（mod p）] （5）

得到快速数论变换（NTT）的公式为：

[Xk=n=0N-1xn（rN）nk（mod p），    0≤k≤N-1] （6）

NTT的逆变换（INTT）公式为：

[xn=1Nk=0N-1Xk（rN）-nk（mod p），    0≤n≤N-1] （7）

选择在有限域[ZpZ]下运算，[p]是一个素数。通过选择一个适当的质数[p]，模乘法在有限域可以进行快速运算。对于FHE算法，选择Solinas素数[5]，[p=][264-232+1]。质数[p]具有特殊的性质，如[296mod p=-1]，[264mod p=232-1]。式（6）中，[rN]是第[N]个的单位圆解[6]。在进行卷积计算时，为了保证最终结果不溢出，则[N2（b-1）2

2.1  基?16NTT算法

在有限域[ZpZ]中，在硬件设计实现NTT的过程中模加、模减、模乘都是基于2的幂次方[7]，如果实现的是64位宽的操作，则每一个运算结果都要进行模[p]操作，占用了大量的硬件资源。所以将64位扩展为192位，采用“零填充”的方式进行数据位的扩展，这样就避免了每次操作都进行模[p]操作[8]，而且有[2192mod p=（212）16mod p=1]。本设计选择16点NTT作为基本单元，运算过程中不需要乘法，只需要移位和模加操作。4 096是第16个单位圆解，16点有限域NTT和INTT公式为：

[X（k）=n=015x（n）212·nk%192mod p] （8）

[x（n）=116k=015X（k）2（192-12nk）%192mod p] （9）

正如前面所提到的，有限域NTT的主要优点是计算不需要乘法，只需要模加法和移位操作。图1给出了一个基数16的FFT体系结构示意图，由图1可见，该基数16的FFT模块包含了16个移位寄存器和16个处理单元。各处理单元包括大量进位保存加法器电路来累加中间结果。在每个时钟周期，16个样本被发送到基数16的单元，然后移位和累加。流水线架构可以在一个时钟周期加上若干个流水线延迟时钟周期内输出16点FFT结果，这符合高吞吐量设计目标。前期已经对16点NTT进行了设计和实现[9]。

2.2  65 536点NTT算法设计

由于NTT点数取值较大时，如果直接进行计算是很复杂的。这时需要将NTT进行分解，使用4级基数为16的NTT构建这个64K有限域NTT模块，根据NTT分解规则，下面列出了64K点NTT的分解公式。式（10）表示将一个64K点NTT分解为一个16点的NTT与4K点FFT的形式，式（11）将4K点NTT分解为16点与256点NTT的形式，式（12）将256点NTT分解为两级的16点NTT运算。经过这三个公式就能将64K点NTT运算转化为4级的16点FFT运算。

[X（k）=n1=015Wn1k116n2=04 095x（n）Wn2k24 096Wn1k216×4 096] （10）

[X（k）=n1=015Wn1k116n2=0255x（n）Wn2k2256Wn1k24 096] （11）

[X（k）=n1=015Wn1k116n2=015x（n）Wn2k216Wn1k216×16] （12）

3  65 536点NTT硬件设计

在硬件架构上，使用4级基数为16的NTT构建64K点有限域NTT模块，同时，这个模块也可以被用于转换INTT结果。图2为64K点NTT单元的串行架构，该架构中主要包括：ROM单元、RAM单元、数据交换单元、基?16NTT处理单元、地址生产单元、信号控制单元、模乘单元。下面就对每个模块进行说明：

1） ROM单元：在整个系统中需要用到16个ROM，因此，通过调用ROM的IP核可以生成16个IP资源，每个ROM的数据深度为4 096，数据位宽为64 bit。ROM里储存计算NTT和INTT所需的旋转因子[10]，旋转因子预先通过C语言编写的代码计算好，然后存储到ROM里。

2） RAM单元：在本设计中RAM结构选用的是具有独立读写地址和读写使能信号的双口RAM，这样可以有利于提高数据的读写效率，节省了运算时间[11?13]。每个RAM的数据深度为4 096，数据位宽为64 bit。

3） 数据交换单元：在数据进行处理之前，对数据重新进行排序，数据处理之后也要进行排序，然后存储到RAM单元中。

4） 地址生成单元：对于本设计的64K点NTT方案来说，初始数据以每4 096个为一组分别存入到16个RAM存储器中。64K点NTT序列抽取按照倒序输入顺序输出的方案进行地址抽取，根据第一级运算中抽取间隔为4 096，第二级抽取间隔为256，第三级抽取间隔为16，第四级抽取间隔为1这个规律进行读取，每16个为一组，一共4 096个周期。若存入同一个存储器中则会导致地址冲突，所以需要将同一组的数据存放在不同的存储器中。根据FFT无冲突地址思想[14]，可以将64K个数据进行存储，如式（13），式（14）所示：

[blockNumber=（[d15+d14+d13+d12]+                  [d11+d10+d9+d8]+[d7+d6+d5+d4]+                  [d3+d2+d1+d0]） mod 16] （13）

[Address=[d15，d14，…，d4]] （14）

式中，[d15，d14，…，d0]為原始序列的编号，原序列共有64K个，因此可以使用16位二进制数的地址来表示。

5） 模乘单元：两个64位数相乘为128位，模乘单元利用模[p]的性质将128位数化简为32位数的相加和相减。

4  实验结果分析

本文在CPU平台和FPGA平台分别实现了64K点有限域NTT算法，使用的CPU平台是Intel? coreTM i7?7700处理器，其主频为3.4 GHz，内存为64 GB，操作系统为Ubuntu 16.04，使用GMP和NTL库上实现64K点有限域NTT算法。在FPGA上使用的是Stratix?V 5SGXEABN2F45I2，设计软件使用的是QuartusⅡ 13.0和ModelSim 10.4软件，运行该结果与GMP运算库进行比较，验证了有限域64K点NTT算法的正确性，最后利用Altera synthesize tool对其进行综合，综合结果如表1所示。

FPGA工作在123.78 MHz下，64K点有限域NTT运算的速度是在CPU下运行的60倍左右，如表2所示。

5  结  语

本文设计并实现了基于FPGA的有限域NTT算法，有限域NTT计算的优势在于只通过使用移位与加法操作就可以实现NTT运算。本文利用16点NTT搭建了64K点NTT单元，通过调用Quartus Ⅱ中的ROM以及RAM存储器IP核，分别用来存储旋转因子和中间过程的数据。采用4级16点NTT处理模式，设计了NTT无冲突地址进行中间计算数据的存取，完成了64K点NTT计算。最终，64K点NTT运算单元在Altera的Stratix?V综合实现，最高处理频率为123.78 MHz，运算速度是在CPU上实现的60倍，因此在信息安全领域具有很高的使用价值。

注：本文通讯作者为黄新明。

参考文献

[1] 段新东.基于密文操作的云平台数据保护技术研究[J].现代电子技术，2016，39（11）：90?94.

[2] 吕琴.云计算环境下数据存储安全的关键技术研究[D].贵阳：贵州大学，2015.

[3] GENTRY C， HALEVI S. Implementing Gentry′s fully?homomorphic encryption scheme [C]// International Conference on Theory and Applications of Cryptographic Techniques： Advan?ces in Cryptology. Tallinn， Estonia： Springer， 2011： 129?148.

[4] GENTRY C. A fully homomorphic encryption scheme [D]. California： Stanford University， 2009.

[5] SOLINAS J A. Generalized Mersenne numbers [J]. Journal of Jishou University， 1999， 38（1/2）： 103?109.

[6] 徐鹏，刘超，斯雪明.基于整数多项式环的全同态加密算法[J].计算机工程，2012，38（24）：1?4.

[7] 林如磊，王箭，杜贺.整数上的全同态加密方案的改进[J].计算机应用研究，2013，30（5）：1515?1519.

[8] WANG W， HU Y， CHEN L. Accelerating fully homomorphic encryption using GPU [C]// High Performance Extreme Compu?ting. Waltham， USA： IEEE， 2013： 1?5.

[9] 施佺，韩赛飞，黄新明，等.面向全同态加密的有限域FFT算法FPGA设计[J].电子与信息学报，2018，40（1）：57?62.

[10] MACINDOE G， MAVRIDIS L， VENKATRAMAN V， et al. HexServer： an FFT?based protein docking server powered by graphics processors [J]. Nucleic acids research， 2010， 38（5）： 445?449.

[11] BRISARD S， DORMIEUX L. FFT?based methods for the mechanics of composites： a general variational framework [J]. Computational materials science， 2010， 49（3）： 663?671.

[12] 占席春，蔡费杨，王伟.多路并行FFT算法的FGPA实现技术[J].现代电子技术，2015，38（19）：34?39.

[13] JOHNSON L G. Conflict free memory addressing for dedicated FFT hardware [J]. IEEE transactions on circuits and systems II： analog and digital signal processing， 1992， 39（5）： 312?316.

[14] 马余泰.FFT处理器无冲突地址生成方法[J].计算机学报，1995，18（11）：875?880.