基于LSSVR提升小波的伽马辐照信号降噪研究

刘瑞 张良力 何笠

摘  要： 采用雪崩光电二极管（APD）作为转换器件采集的伽马辐照信号，呈现出明显的非平稳随机性，并掺杂有大量的噪声信号，为解决此问题，提出了基于最小二乘支持向量机回归（LSSVR）提升小波的伽马辐照信号降噪算法。用剖分信号建立训练样本，以最小均方误差为目标，通过LSSVR非线性拟合构造预测算子，实现伽马辐照信号的降噪处理。实验用伽马辐照信号采集系统，采用碘化铯（CsI）闪烁体耦合APD作为探测前端，为放大探测信号并稳定增益，设计了前端读出电路和APD温度补偿偏压控制电路。相较于其他降噪算法，所提算法对伽马辐照信号分解层数少，细节保留好，时间复杂度低，降噪后伽马辐照信号信噪比高，可提高伽马辐照探测系统的能量分辨率，优化辐照强度测量及其能谱分析。

关键词： 伽马辐照信号; 信号降噪; LSSVR提升小波; 信号分解; 信号采集; 电路设计

中图分类号： TN911.6?34; TP391                    文献标识码： A                   文章编号： 1004?373X（2020）09?0041?05

Research on gamma irradiation signal noise reduction based on LSSVR lifting wavelet

LIU Rui， ZHANG Liangli， HE Li

（School of Information Science and Engineering， Wuhan University of Science and Technology， Wuhan 430081， China）

Abstract： When avalanche photodiode （APD） is taken as the conversion device to collect the gamma irradiation signal， obvious non?stationary randomness occurs and the signals are mixed with a large number of noise signals. In order to solve the problem， a gamma irradiation signal noise reduction algorithm based on lifting wavelet with least square support vector machine regression （LSSVR） is proposed. A training sample is created with the split signal， and a prediction operator is constructed by LSSVR nonlinear fitting to achieve the noise reduction processing of the gamma irradiation signal， so as to minimize the mean square error （MSE）. In the gamma irradiation signal acquisition system for test， cesium iodide （CsI） scintillator coupled APD is taken as the detection front end to design the front end readout circuit and APD temperature compensation bias control circuit for the amplification of detected signals and the stabilization of gain. In comparison with other noise reduction algorithms， the proposed algorithm for the gamma irradiation signal are of fewer decomposition layers， better detail reservation， lower level of time complexity and higher signal?to?noise ratio （SNR） after noise reduction processing， and can improve the energy resolution of gamma radiation detection system， and optimize the irradiation intensity measurement and the energy spectrum analysis.

Keywords： gamma irradiation signal; signal noise reduction; LSSVR lifting wavelet; signal decomposition; signal acquisition; circuit design

0  引  言

伽马辐照信号中掺杂的噪声类型包括：热噪声、散粒噪声、背景噪声等[1]。噪声信号会掩盖伽马辐照信号的幅度、峰峰值等有效信息，降低探测系统能量分辨率，对辐照强度测量及能谱分析产生不利影响。在伽马辐照信号分析处理过程中，信号降噪是一个关键步骤。伽马辐照信号呈现出明显的非平稳随机性，对于此类型信号的降噪，国内外学者提出许多方法，如中值滤波法、经验模态分解法（EMD）、小波变换法等。中值滤波法易造成信号不连续;EMD对极值点分布不均匀的信号进行滤波时，可能导致模态混叠，从而使IMF分量失去原本应有的物理意义;小波变换法在自身构造及对信号进行“时?频?时”变换时，占用大量系统资源，且运行速度慢，不能很好地满足实时性要求[2]。本文研究的提升小波去噪算法，是一种独立于Fourier变换的提升时域变换[3]，可实现信号降噪时的原位运算和实时运算，减少小波分解层数，降低小波分解计算复杂性。

1  基于LSSVR提升小波算法

构建算法时，需在提升小波中引入最小二乘支持向量机回归（LSSVR），用剖分信号建立训练样本，以最小均方误差为目标，通过LSSVR非线性拟合的方法构造预测算子。假设辐照探测器输出信号[X={x（k），k∈Z}]，基于LSSVR提升小波变换的信号分解过程包括分裂、预测和更新三个部分[3?4]，具体实现步骤如下：

1） 分裂：将信号[X]分为偶序列[xe（k）]和奇序列[xo（k）]两个部分。

[xe=x（2k），   xo=x（2k+1），   k∈Z]  （1）

2） 预测：通过LSSVR提升小波，用偶序列[xe（k）]来估计奇序列[xo（k）]，并用预测误差作为细节信号。用相邻2[N]个偶序列生成[N]维左相空间[xe（k）N]和[N]维右相空间[x′e（k）N]。

[xe（k）N=（xe（k-N+1），xe（k-N+2），…，xe（k））] （2）

[x′e（k）N=（xe（k+1），xe（k+2），…，xe（k+N））] （3）

将[xe（k）N]和[x′e（k）N]作为预测部分输入值[xk]和[x′k]，奇序列[xo（k）]为[yk]。给定[N]个左训练集[{xk，yk}]和[N]个右训练集[{x′k，yk}]，基于LSSVR估计可归结为如下优化式子[5?7]：

[minω，eJ（ω，e）=12ωTω+12γk=1ne2ks.t.    yk[ωTφ（xk）+b]=1-ek，    k=1，2，…，N] （4）

式中：[φ（xk）]为[Rn→Rd]的空间映射函数;[ω∈Rd]为权值向量;[γ]为正则化参数，控制对误差的惩罚程度;[ek]为预测误差;[b]为偏差量。求解的问题为约束条件下最小值优化问题。试构建拉格朗日辅助函数：

[L（ω，b，e，λ）=J（ω，e）-k=1Nλk{yk[ωTφ（x）+b]-1+ek}] （5）

式中[λk]为拉格朗日乘子。

分别对式（5）中[ω，b，e，λ]求偏微分，令各偏微分式为0，构建方程，消去[ω]和[e]，解方程可得：

[LSSVR（x）=             k=1NλkykK（x，xk）+b1+k=1NλkykK（x，x′k）+b22] （6）

式中[K（x，xk）]为核函数，用于将低维数据映射到高维空间。当输入为[xe（k）]，那么[xo（k）=LSSVR（xe（k））]，预测误差为：

[d（k）=xo（k）-xo（k）] （7）

为满足尺度自适应的原则，约束准则为：

[min Z=k=1Nd2（k）]   （8）

3） 更新：用[N]个（[N]为偶数）小波细节信号来更新偶序列，令[N=N]时，更新算子系数[8]为其对应的预测算子的[12]，[c（k）]即为小波的逼近信号。

[c（k）=xe（k）+12LSSVR（d（k））]   （9）

基于LSSVR提升小波的优点是把传统的滤波器问题分解为一些基本的构造步骤，每一步都可逆，重构过程与分解过程相反[9]。采用上述步骤可摆脱传统提升小波线性预测算子的局限性，能较好地保留伽马辐照信号细节，同时实现信号降噪处理。

2  伽马辐照信号采集系统的设计

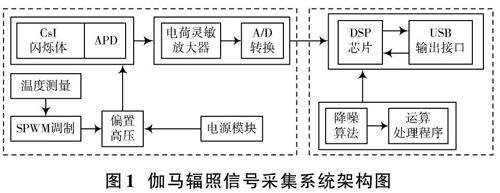
作为光电探测器件，APD具有工作稳定可靠、响应时间短、工作频率高等优点[10]。伽马辐照信号采集系统采用CsI闪烁体耦合APD作为探测前端，系统由探测前端、前端读出电路、DSP控制及处理单元、APD温度补偿偏压控制电路組成。伽马辐照信号采集系统架构如图1所示。

2.1  前端读出电路

由于探测前端输出信号电流较小，需要前端读出电路对信号进行放大并进行模/数（A/D）转换供后续DSP控制及处理单元读取。此部分包括电荷灵敏放大电路（CSP）和A/D转换电路。CSP采用计数通过率高、无直流漂移现象的交流耦合方式来设计[11]，如图2所示。A/D转换直接使用低功耗ADC芯片进行设计。

CSP采用三级设计结构。前级采用JFET组成共源极放大电路，提取微弱的APD输出信号。偏置电阻（[R8]，[R9]，[R17]）和电容[C8]构成放电回路，其时间常数[τ1=（R4+R8+R9）×C8];反馈电阻（[R19]，[R20]，[R21]）和反馈电容[C14]构成放电回路，时间常数[τ2=（R19+R20+R21）×C14];后级微分成形电路（[R7]，[C6]）的时间常数[τ3=R7×C6]，保证[τ3]远小于[τ1]和[τ2]，这样才能保证CSP输出信号无零极点。[C8]和CSP的等效电容形成电容分压的关系，一般设置为10 nF。考虑到APD结电容与JFET的输入电容相匹配，输出信号信噪比高[12]，选择JFET时与CSP进行电容匹配。中间级采用共基级放大电路，[R1]，[R3]和Q1构成恒流源，[R14]，[R15]和Q3也构成恒流源，两个恒流源的设计保证流过JFET的电流在其允许的漏电流[Idss]范围内。[R3]，[R6]，[R15]也构成偏置电阻，用来设定合适的静态工作点。[R1]，[R3]和Q1构成的恒流源成了三极管Q4的有源负载，提高了系统的稳定性和开环增益。

为了使输出信号进一步放大，输出级采用AD8065运算放大器。为防止后级运算放大器满幅度过载，在运放前加入了CR微分整形电路。经过实际测试，CSP能有效放大信号，运放输出电流最高可达几百毫安，可安全驱动ADC芯片。

2.2  APD温度补偿偏压控制电路

前端输出的脉冲信号幅度与APD内置增益、APD两端偏置电压相关[13]。偏压过低时，电流增益也過低，APD不能发挥最佳性能，偏压过高时，噪声随之增大，信号会被湮没而影响信号提取[14]。查阅某型号APD在固定波长[λ]=420 nm光照下，其雪崩增益[G]随偏压值、温度值的变化关系如图3所示。

为采集到稳定有效的伽马辐照信号，必须保证在不同温度下，APD增益和输出脉冲幅度稳定，故有必要对APD进行温度补偿偏压控制。由APD数据手册可知，其增益在40～60之间时，信号输出幅度最好。取增益[G=]50作为基准线，分别与20 ℃，60 ℃曲线相交于[A]，[B]点，过[A]点作切线，切线方程为[G1（x）=k1x+b1]，保持[k1]不变，将切线平移至[B]点，得[G2（x）=k1x+b2]，假设不同温度的APD增益曲线在[AB]之间均匀分布，可构建如下增益平移解析式：

[G（x）=k1x+（b1-b2）（Tc-20）] （10）

式中[Tc]为当前温度。当增益、当前温度给定时，APD偏压值即可根据式（10）计算得出。

利用Matlab/Simulink设计基于平移解析式的APD温度补偿控制偏压仿真电路。该电路包含“直?交?直”升压电路和电压、电流双闭环PID调节两部分，可根据温度值实时调节电路输入电压，从而输出补偿偏压值，仿真电路如图4所示。

在本次研究中，PID controller参数[P=]3，[I=]20，[D=]8;PID controller1参数[P=]0.303 5，[I=]50，[D=]0，电压输出[Uo]与输入[Ui]关系为：

[Uo=Ui12×400] （11）

在20 ℃，给定输入电压为10 V时，输出偏压随时间的变化如图5所示。

实际电路依据仿真电路的双闭环控制逻辑来设计，经过APD温度补偿控制电路的调节，在不同温度下使用示波器观察APD输出信号幅度，得到信号增益随温度变化的曲线如图6所示。

可以看出，采用APD温度补偿偏压控制后，APD增益幅度稳定在40～60之间，且无明显波动，符合控制要求，利于后续的信号降噪。

3  实验分析

3.1  数据采集

在距离某实体伽马辐照源10 cm处（仪表显示均值4.5 μSv/h），利用设计开发的伽马辐照信号采集系统采集信号，得到未经处理的伽马辐照信号如图7所示。

3.2  LSSVR提升小波分解

对伽马辐照信号进行LSSVR提升小波分解，维度2[N]取6，训练数据长度为1 000，核函数选线性核函数[k（x，xk）=xTkx]，分解层数为2，分解后细节信号和近似信号如图8所示。可以看出，第二层近似信号中的噪声得到了很好的抑制，表明基于LSSVR构造的预测算子能反映出信号特征，近似信号所含的噪声信息少，整个过程只需2层分解即可起到明显的抑制噪声效果。

3.3  降噪效果对比分析

将未经处理的伽马辐照信号，使用中值滤波、EMD滤波、db4小波（软阈值）滤波、sym4小波（默认值）滤波、传统db4提升小波进行降噪处理，其效果与基于LSSVR的提升小波变换滤波效果如图9所示。

图9中，db4、sym4、传统db4提升小波和LSSVR提升小波采用2层分解降噪，软阈值处理函数为：

[d=0，     d≤λsgn（d）d2-λ2，      d>λ] （12）

[λ=σ2ln（length（x））] （13）

式中[σ]为噪声的偏差估计。

从图9中可知：中值滤波降噪效果不佳，噪声未得到很好的抑制;EMD降噪采用了6层分解，各模态分量在重构时，受噪声干扰改变了原始信号;db4小波和sym4小波在只有2层分解条件下，降噪效果有限，不能很好地去除噪声信号;传统提升小波降噪效果明显，但重构后出现毛刺现象;LSSVR提升小波降噪明显，且信号细节保留较好。

为定量分析降噪效果，引入信噪比（SNR）和均方根误差（RMSE）评价降噪后的信号。降噪后，新的信号SNR值越高、RMSE值越小，则表明它更接近于原始信号，有更好的去噪效果[15]。定义信噪比（SNR）为：

[SNR=10logk=1nx2（k）k=1n[x（k）-x（k）]2]   （14）

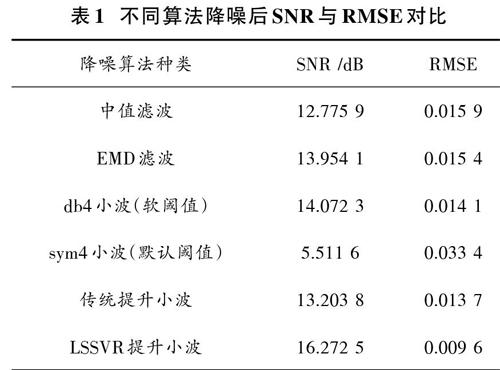
采用上述不同方法降噪后，信号SNR和RMSE如表1所示。可以看出，基于LSSVR提升小波2层分解降噪后，效果最好。

3.4  能量分辨率

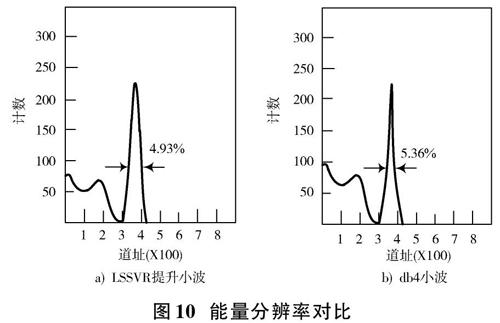
能量分辨率是衡量能否将两个能量相近的射线分开的主要因素[16]，是表征电离辐射探测器性能的一个重要指标，数值越小反映对能量的分辨率越高。经db4小波（软阈值）法和LSSVR的提升小波降噪后的信号在同一条件（温度20 ℃，探测距离10 cm）下进行能量分辨率对比（如图10所示）可知，后者能量分辨率为4.93%，优于前者的5.36%，表明采用基于LSSVR提升小波降噪处理后的伽马辐照探测器对相近能量伽马峰值的分辨能力更强，信号探测更灵敏。

3.5  实时性分析

随机选取一段测量信号，对6种降噪算法的时间复杂度进行测试，所用时间如表2所示。

经比对，本文所提出的LSSVR提升小波实时性优于EMD滤波、db4小波（软阈值）滤波、sym4小波（默认值）滤波，劣于中值滤波、传统db4提升小波。但随着伽马辐照信号数据量的增大，以及小波分解层数的增加，基于LSSVR提升小波的降噪效果和运算效率综合优势将逐步凸显。

4  结  论

本文对伽马辐照信号降噪过程进行了研究。设计的前端读出电路和APD溫度补偿偏压控制电路，能有效放大伽马辐照信号并稳定增益，为后续信号降噪创造了必要条件。构建了基于LSSVR提升小波降噪算法，对实验采集的伽马辐照信号进行2层分解降噪，降噪后信噪比为16.272 5，均方误差为0.009 6。相较于其他降噪算法，LSSVR提升小波算法在同等条件下，信号分解层数少，降噪后信号细节保留较好，运算效率较高。

算法在能量分辨率及运算效率方面可进一步优化，相关研究工作将在后续展开。

注：本文通讯作者为张良力。

参考文献

[1] 刘贺雄，周冰，高宇辰.APD探测系统的噪声特性及其影响因素研究[J].激光技术，2018，42（6）：862?867.

[2] 孟明，鲁少娜，马玉良.基于EEMD与改进提升小波的脑电信号消噪方法[J].计算机工程，2016，42（4）：313?317.

[3] 谈恩民，王存存，张欣然.基于小波变换和CFA?LSSVM模拟电路故障诊断[J].电子测量与仪器学报，2017，31（8）：1207?1212.

[4] 张鹏，倪世宏，谢川，等.提升小波尺度自适应非线性算子构造方法[J].中南大学学报，2012，43（3）：992?996.

[5] SUYKENS J A K， VANDEWALLE J. Least squares support vector machine classifiers [J]. Neural processing letter， 1999， 9（3）： 293?300.

[6] 张爱华，霍星，张志强.多核自适应迭代LSSVR的模拟电路性能评价策略[J].电子测量与仪器学报，2013，27（2）：115?119.

[7] JAYADEVA， KHEMCHANDANI R， CHANDRA S. Regularized least squares twin SVR for the simultaneous learning of a function and its derivative [C]// 2006 International Joint Conference on Neural Networks. Vancouver， BC， Canada： IEEE， 2006： 1192?1197.

[8] 张鹏，倪世宏，谢川.基于LSSVR的提升小波自适应算子构造方法与应用[J].火力与指挥控制，2012，37（9）：35?38.

[9] 鞠薇，鲁昌华，张玉钧，等.改进阈值提升小波和自适应滤波器的开放光路红外光谱去噪[J].光谱学与光谱分析，2018，38（6）：1684?1690.

[10] 董伟波，王茜蒨，韩旭.基于虚拟仪器技术的APD噪声等效功率测量系统[J].仪器仪表学报，2011，32（11）：2635?2640.

[11] 曾国强，魏世龙，夏源，等.碲锌镉探测器的数字核信号处理系统设计[J].核技术，2015，38（11）：49?56.

[12] 解超.基于InCaAs/InP APD单光子探测器的研究[D].武汉：华中科技大学，2016：8?13.

[13] 胡浪，张开琪，曾国强，等.CsI（Tl）晶体的APD前端读出特性研究[J].核技术，2016，39（10）：41?45.

[14] 李维康，申华，王寿增.APD偏压的环境自适应数字控制技术研究[J].光学与光电技术，2018，16（1）：39?46.

[15] 李红延，周云龙，田峰，等.一种新的小波自适应阈值函数振动信号去噪算法[J].仪器仪表学报，2015，36（10）：2200?2206.

[16] 石亚星，张流强，何艳，等.多通道能谱分析系统的通道复用技术[J].电子测量技术，2016，39（11）：151?154.