地下水位回升对地铁隧道围岩稳定性的影响
2020-06-19魏月
魏 月
(山东省地矿工程勘察院,山东 济南 250000)
随着城市建设的不断扩大,城市地面可利用空间逐年减少,导致地下空间开发利用越来越多[1]。近年来,地下工程建设快速发展,工程规模越来越大,地下结构越来越复杂,对地下水的控制也越来越严格,由地下水带来的安全问题越来越多[2]。因此,地下水对城市地铁隧道建设的影响受到不少学者的重视,包括地下水对隧道施工的安全、后期运营的影响,总结出了不少应用型成果[3]。随着地下工程建设的增多,以及近年来我国对地下水资源的保护,地下水位有回升趋势,但其对地下结构的影响,几乎很少有人关注,对这方面的研究不足,导致很多由于地下水位回升引起的灾害无从下手[4]。国际上已经有学者开始重视对水位回升影响地下结构的研究,英、美、法、日等国家均出现由于地下水位回升引起工程灾害,如英国伯明翰市有的建筑物基础被淹没、利物浦不列颠铁路隧道抽出水量增大、伦敦市附近地下水位年上升量约1.5m、泰晤士河岸砂岩地基上的建筑物地下室充水现象十分普遍等[5]。文章基于对已有地铁隧道地下水位回升监测数据,借助有限元数值分析方法,研究了水位回升过程隧道围岩应力应变变化,以确保隧道围岩的安全、稳定。
1 工程背景
以上海地铁某线为工程研究背景,拟建地铁隧道埋深在14.0~21.0m,区间隧道地层主要为黏性土;开挖施工期间,地下水位较高,一般水位在0.5~1.5m,隧道底板下存在承压水,承压水头在5.0~18.0m,施工期间采取了有效降水措施。隧道直径6.0m,拟研究区间段拱顶埋深约15.0m,地下水初始水位在隧道底板以下3.0m,隧道主轴线主要穿越淤泥质粉质黏土及灰色黏性土。场地内岩土层概况主要为杂填土、粉质黏土、淤泥质粉质黏土、淤泥质黏土、黏土、粉质黏土及粉细砂,黏性土趋于软塑,其自稳性质较差,力学性质相对不良。
2 建立有限元模型
以该地铁隧道线路实际地质性质作为模型的原型,同时考虑隧道围岩边界效应及条件考虑,开挖掘进方向进尺取2.0m,采用ANSYS有限元分析计算软件,建立二维有限元模型,如图1所示[6]。

图1 有限元计算模型图
根据实际计算原则,对拟建隧道围岩力学参数进行适当调整,使其更加接近实际情况[7]。有限元计算本构模型采用摩尔库伦等效应力圆准则,相应原理如下[8]:

式中:σ1为主应力;σ2、σ3为次应力;ψ为内摩擦角;τ为剪切应力。
地铁隧道衬砌采用线性单元,采用ANSYS单元生死技术模拟隧道开挖,左右线交叠台阶式开挖,每一步开挖完后紧接着做初次支护,二次衬砌作为安全储备,本文不做研究。各岩土参数如表1所示。
根据预先设定好的地下水位回升情况,模拟实际地下水回升情况,在有限元数值模型中设置地下水位回升条件,分别以3.0m、6.0m、9.0m三种水位工况下隧道围岩应力应变情况进行计算。
3 数值计算结果分析
根据上述设计的水位工况,模拟计算水位回升过程及结束时隧道围岩安全稳定性,分别从应力、应变两方面进行分析,研究其变化规律,进而分析水位回升对隧道围岩结构和周边环境的影响。
3.1 竖向位移变化规律
隧道围岩在不同水位工况情况下,对应的隧道竖向位移变化规律曲线如图2所示。从图2中可以看出,随着地下水位的提升,隧道围岩与地表总体有向地上产生位移的趋势,且地表产生的位移量最大,拱顶围岩位移量大于拱底围岩位移量,可以看出地下水的变化对隧道围岩随着标高的提升,影响逐渐变大。分析原因可知,地下水位回升,对隧道底板产生浮力作用,隧道整体上浮,地表产生回弹变形。

表1 下穿土层物力力学参数表

图2 地下水位标高与隧道竖向位移关系曲线图
地下水位回升对隧道侧壁的变形影响如图3所示。当地下水位从初始水位回升至隧道底板时,此时地下水位并未对隧道产生上浮力作用,但隧道底板以下持力层孔隙水压力增加,促使土层发生回弹变形,所以隧道和地下土层均会产生向上的位移的趋势,隧道结构自身变形较小,隧道顶板、底板及地表初始竖向变形基本形同。
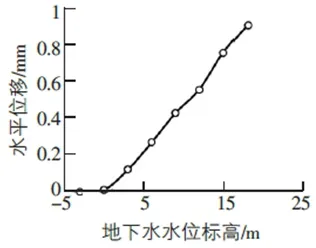
图3 地下水位标高与隧道侧壁水平位移关系曲线
随着地下水位的持续上升,直至上升到隧道围岩顶部时,地下水对隧道结构整体产生上浮作用,土层孔隙水压力增加,进而使土层产生更大的变形,隧道首先表现的是整体上升。从图2、图3中可以看出,隧道整体上浮量达到0.7cm,因为隧道拱顶、拱底孔隙水压力不同水压不同,所以隧道拱顶、拱底位移量不同。随着地下水的升高,隧道围岩侧壁压力增加,隧道自身产生一定的变形,导致地层也会发生相应的重新组合变形。当地下水位回升到地表位置时,隧道顶板的竖向位移约2.2cm,隧道底板的位移为2.0cm。
3.2 隧道围岩水平向位移
地下水位回升的三种工况对应的隧道围岩水平向的位移与水位变化曲线如图3所示。从图3可以看出,当地下水位位于隧道拱腰以下时,水平位移几乎不会产生;当地下水位升至拱腰以上时,随着水位的持续回升,位移持续增加,最大水平位移约0.9cm,隧道围岩侧壁整体位移不大,对隧道的稳定性影响不大[9]。
3.3 隧道围岩结构内力变化规律
隧道围岩所处的地下环境发生变化,其应力应变场必然发生相应的变化。根据上文建立的数值计算模型,计算地下水位上升过程中隧道围岩结构应力、应变场,得出了隧道围岩结构应力变化规律。
随着隧道围岩周边地下水位的回升,隧道侧壁部分应力逐渐增加,其负弯矩相应增加,拱顶、拱底正弯矩增大,受力变化最大点位于隧道拱腰部位;随着地下水位的继续回升,土体有效应力减小,孔隙水压力增加,隧道侧壁负弯矩及拱底、拱顶正弯矩逐渐减小。虽然最大弯矩减少了,但隧道围岩结构可能发生负弯矩的转换,将与设计弯矩产生反向逆差,对结构的安全稳定性不利。
4 结束语
文章以上海地区某线地铁隧道建设为工程背景,借助有限元数值计算方法,模拟计算了地下水位回升过程中隧道结构的变化,并从隧道结构应力、应变两方面分析了其对地铁隧道安全稳定性的影响,揭示了地下水位回升与隧道围岩结构应力、应变的变化规律及关系。通过研究表明,地下水位回升到一定高度后,随着水压力的增加,其对地铁隧道围岩结构的安全稳定性会产生不利影响,应引起重视。
